Magnetische inductieformules, hoe het wordt berekend en voorbeelden

De magnetische inductie of magnetische fluxdichtheid is een wijziging van de omgeving veroorzaakt door de aanwezigheid van elektrische stromen. Ze wijzigen de aard van de omliggende ruimte, waardoor een veld Vector.

De vector Magnetische inductie, magnetische fluxdichtheid Of gewoon magnetisch veld B, Het heeft drie onderscheidende kenmerken: een intensiteit die wordt uitgedrukt door een numerieke waarde, een adres en ook een gevoel gegeven op elk punt in de ruimte. Het wordt vetgedrukt gemarkeerd om het te onderscheiden van puur numerieke hoeveelheden of scalair.

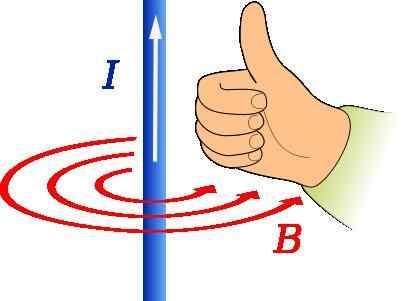Rechter duimregel om de richting en richting van de magnetische inductievector te bepalen. Bron: JFMelero [CC BY-SA 4.0 (https: // creativeCommons.Org/licenties/by-sa/4.0)]

De rechter duimregel wordt gebruikt om de richting en richting van het magnetische veld te vinden die is ontstaan ​​door een draad die stroom transporteert, zoals weergegeven in de bovenstaande figuur.

De duim van de rechterhand moet in de richting van de stroom wijzen. Dan geeft de beurt van de resterende vingers de vorm aan van B, dat in de figuur wordt weergegeven door de concentrische cirkels van rood.

In dit geval is het adres van B Het is tangentieel voor de concentrische omtrek met de draad en de betekenis is in strijd met de klokken.

De magnetische inductie B In het internationale systeem wordt Tesla (T) gemeten, maar het is vaker voor om het te meten in een andere eenheid genaamd Gauss (G). Beide eenheden werden respectievelijk benoemd ter ere van Nikola Tesla (1856-1943) en Carl Friedrich Gauss (1777-1855) voor hun buitengewone bijdragen aan de wetenschap van elektriciteit en magnetisme.

[TOC]

Wat zijn de eigenschappen van magnetische inductie of magnetische fluxdichtheid?

Een kompas dat met de stroom in de buurt van de draad wordt geplaatst, zal altijd aansluiten bij B. Deense fysicus Hans Christian Oersted (1777-1851) was de eerste die dit fenomeen realiseerde aan het begin van de 19e eeuw.

Kan u van dienst zijn: Areolaire snelheid: hoe het wordt berekend en opgeloste oefeningen

En wanneer de stroom ophoudt, wijst het kompas naar het geografische noorden, zoals altijd. Door de positie van het kompas zorgvuldig te veranderen, wordt een kaart verkregen uit de magnetische veldvorm.

Deze kaart heeft altijd de vorm van concentrische cirkels voor de draad, zoals in het begin beschreven. Op deze manier kan het worden gevisualiseerd B.

Zelfs als de draad niet recht is, de vector B zal concentrische kringen eromheen vormen. Om te bepalen welke vorm het veld heeft, is het voldoende om zich zeer kleine draadsegmenten voor te stellen, zo klein dat ze rechtlijnig lijken en omgeven door concentrische omtrek.

Magnetische veldlijnen geproduceerd door een draadlus die stroom transporteert. Bron: Pixabay.com

Dit duidt op een belangrijke eigenschap van de magnetische veldlijnen B: Ze missen principe of eindigen, het zijn altijd gesloten krommen.

De biot-savartwet

De negentiende eeuw bepaalde het begin van het tijdperk van elektriciteit en magnetisme in de wetenschap. Nabij het jaar 1820 ontdekten de Franse natuurkundige fysici Jean Marie Biot (1774-1862) en Felix Savart (1791-1841) de wet die zijn naam draagt ​​en die het mogelijk maakt om de vector te berekenen B.

Ze deden de volgende observaties over de bijdrage aan het magnetische veld geproduceerd door een differentiële lengte draadsegment DL Dat transporteert een elektrische stroom Je:

• De omvang van B neemt af met het omgekeerde tot het kwadraat van de afstand tot de draad (dit is logisch: ver van de draad de intensiteit van B Het moet minder zijn dan in nabijgelegen punten).
• De omvang van B Het is evenredig met de intensiteit van de stroom Je Dat reist op de draad.
• Het adres van B Het is tangentieel voor de radiomomtrek R gecentreerd op draad en de richting van B Het wordt, zoals we hebben gezegd, gegeven door de juiste duimregel.

Het vector- of productkruisproduct is het juiste wiskundige hulpmiddel om het laatste punt uit te drukken. Om een ​​vectorproduct op te zetten, zijn twee vectoren nodig, die als volgt worden gedefinieerd:

• Dl Het is de vector waarvan de grootte de lengte van het differentiaalsegment is DL
• R Het is de vector die van de draad naar het punt gaat waar u het veld wilt vinden

Kan u van dienst zijn: elektromagnetisch spectrum: kenmerken, banden, toepassingen

Formules

Dit alles kan worden gecombineerd in een wiskundige uitdrukking:

De evenredigheid constant die nodig is om gelijkheid vast te stellen is Magnetische permeabiliteit van vrije ruimte μ_of  = 4π.10^-7 T.m/a

Deze uitdrukking is de wet van Biot en Savart, waarmee u het magnetische veld van een stroomsegment kunt berekenen.

Een dergelijk segment moet op zijn beurt deel uitmaken van een groter en groter circuit: een stroomverdeling.

De voorwaarde dat het circuit is gesloten, is nodig om een ​​elektrische stroom te laten stromen. Elektrische stroom kan niet in open circuits stromen.

Ten slotte worden alle bijdragen van elk differentiaalsegment toegevoegd om het totale magnetische veld van deze huidige verdeling te vinden Dl. Dit komt overeen met het integreren van alle distributie:

Om de biot-savartwet toe te passen en de magnetische inductievector te berekenen, is het noodzakelijk om zeer belangrijke belangrijke punten te overwegen:

• Het vectorproduct tussen twee vectoren resulteert altijd in een andere vector.
• De omvang van het vectorproduct in de biot-savartwet is:waar θ is de hoek tussen Dl En R.
• Het vectorproduct moet worden gevonden voor Als de integrale resolutie is opgelost, wordt de integraal van elk van de afzonderlijk verkregen componenten opgelost opgelost.
• Het is noodzakelijk om de situatie te tekenen en een adequaat coördinatensysteem op te zetten.
• Wanneer het bestaan ​​van sommige symmetrie wordt waargenomen, moet het worden gebruikt om de berekeningstijd te besparen.
• Wanneer er driehoeken zijn, zijn Pythagoras Stelling en Cosine Stelling van grote hulp om de geometrische relatie tussen de variabelen vast te stellen.

Hoe wordt het berekend?

Met een praktisch voorbeeld van de berekening van B Voor rechtlijnige draad worden deze aanbevelingen toegepast.

Het kan u van dienst zijn: PIMPLE LOAD: Eigenschappen en Coulomb Law

Voorbeeld

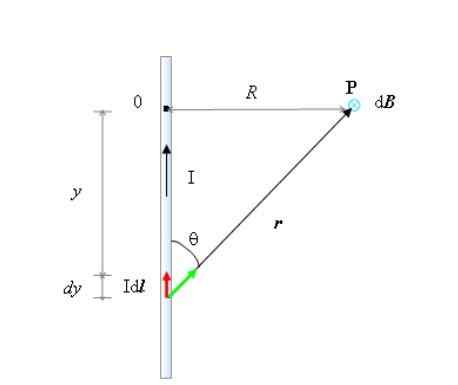
Bereken de magnetische veldvector dat een zeer lange rechtlijnige draad produceert op een punt P van de ruimte, volgens de getoonde figuur.

Geometrie die nodig is om het magnetische veld te berekenen op punt P, van een oneindig lange stroomdraad. Bron: zelf gemaakt.

Uit de figuur moet u:

• De draad wordt verticaal gericht, met de stroom die ik stroomt. Dit adres is +en in het coördinatensysteem, waarvan de oorsprong op punt is of.
• θ is de hoek tussen Dl En R En het is ook waar dat: 
• In dit geval, volgens de juiste duimregel, B Op punt P wordt in het papier gericht, dus het wordt aangeduid met een kleine cirkel en een "x" in de figuur. Dit adres wordt genomen als -z.
• De juiste driehoek waarvan de benen zijn En En R, Relateert beide variabelen volgens de stelling van Pythagoras: R²= R²+En²

Dit alles wordt vervangen in de integraal. Het vector- of kruisproduct wordt aangegeven door zijn grootte plus richting en de betekenis ervan:

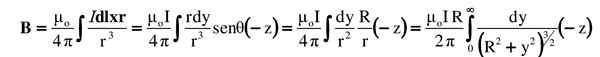
De voorgestelde integrale wordt gezocht in een integrale tabel of wordt opgelost door een geschikte trigonometrische substitutie (de lezer kan het resultaat controleren met behulp van y = rtg θ):

Het resultaat komt overeen met de verwachte: de grootte van het veld neemt af met de afstand R en neemt evenredig toe met de intensiteit van de stroom i.

Hoewel een oneindig lange draad een idealisatie is, is de verkregen uitdrukking een zeer goede benadering van het veld van een lange draad.

Met de biot- en savartwet is het mogelijk om het magnetische veld van andere hoge symmetrieverdelingen te vinden, zoals een cirkelvormige spiraal die stroom transporteert, of gevouwen draden die rechtlijnige en kromlijnige segmenten combineren.

Om de integrale te analyseren, moet het probleem natuurlijk een hoge mate van symmetrie hebben. Anders is het alternatief numeriek het oplossen van de integraal.

Referenties

1. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 2. Mexico. Cengage Learning Editors. 367-372.