Wiskunde

Negatieve homotecia

Negatieve homotecia
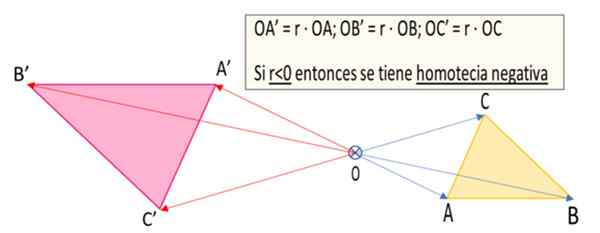
Figuur 1. De driehoek a'b'c 'is de homothetische transformatie van de ABC -driehoek ten opzichte van het punt of met een reden van negatieve homotecia r = -1.5 (opgesteld door: f zapata).

Wat is negatieve homotecia?

Negatieve homotecia is een transformatie waarbij een polygoon in een vlak als beeld een andere polygoon in datzelfde vlak heeft, van gelijke hoeken en met de overeenkomstige zijden die evenredig zijn aan die van het origineel. Wanneer homotecia negatief is, wordt het beeld een halve draai gedraaid ten opzichte van de initiële figuur.

Homotecia wordt gekenmerkt door een Homotecia Center te hebben OF en een evenredigheidsconstante rede genoemd R. Wanneer R Het is een negatief getal, dus er is sprake van negatieve homotecia.

Hoe wordt een homotecia -transformatie gemaakt?

Om uit te leggen hoe een negatieve homotecia wordt uitgevoerd, nemen we het geval van figuur 1 waarin een driehoek is abc die zijn negatieve homothetische wil bouwen.

1.- Het begint een homotecia -centrum te kiezen, dat is dit geval het punt is OF.

2.- Van OF Georiënteerde segmenten zijn gebouwd (vectoren) Oa, OB En OC die van het centrum van Homotecia gaan naar elk van de hoekpunten van de driehoek.

3.- Een Homotecia -reden wordt gekozen R. Zoals je een negatieve homotecia wilt, dan R Het moet minder zijn dan nul. In het geval van figuur 1 werd het genomen R = -1.5.

4.- Vectoren zijn getekend Oa ', Ob ' En Oc ', die respectievelijk zijn Oa '= r ∙ OA, Ob '= r ∙ OB  En Oc '= r ∙ OC. Als R = -1.5, dat is een negatief getal, dan de vectoren Oa ', Ob ' En Oc ' Ze hebben richting in strijd met hun overeenkomstige tegenhangers, dat wil zeggen Oa, OB En OC. Maar als de absolute waarde van de rede R is | R | = 1.5 de afmetingen van Oa ', OB' En Oc ' Ze zijn anderhalve halve meer groter dan die van hun tegenhangers Oa, OB En OC.

5.- De tips van de vectoren Oa ', Ob ' En Oc ' Definieer de hoekpunten van de driehoek A'b'c ' Wat is de negatieve homothetische van de driehoek abc.

Eigenschappen van negatieve homotecia

De Negatieve homotecia, ook wel genoemd Omgekeerde homotecia, Het heeft de volgende eigenschappen:

Het kan u van dienst zijn: veelvouden van 8: wat zijn en uitleg

1.- De overeenkomstige zijden tussen de beeldpolygoon en de oorspronkelijke polygoon hebben proportionele lengtes, die de constante van evenredigheid zijn, de absolute waarde van de homotecia -verhouding, dat wil zeggen dat het beeld wordt versterkt in een factor | R | zo lang als | R | is groter dan de eenheid, maar de afbeelding is verminderd als | R | is minder dan de eenheid.

2.- De hoeken tussen de overeenkomstige zijden van het beeld en de oorspronkelijke figuur hebben dezelfde maatregelen.

3.- De homologe kanten tussen origineel en beeld zijn parallel aan elkaar.

4.- De overeenkomstige segmenten in het geval van negatieve homotecia zijn parallel, maar met begeleiding of tegengestelde richting. In figuur 1 heeft Segment AB bijvoorbeeld zijn homologe a'b 'parallel aan de eerste, maar met de tegenovergestelde richting.

Vergelijking met positieve homotecia

Het wordt positieve homotecia genoemd in welke homotecia -ratio een positief aantal is. Om een ​​positieve homotecia te bouwen, worden dezelfde stappen gevolgd als die van negatieve homotecia:

1.- Kies een Homotecia Center, in ons geval het punt OF (Zie figuur 2).

2.- Teken de georiënteerde segmenten (vectoren), variërend van het centrum van homotecia tot de hoekpunten van de polygoon, in het geval van figuur 2 zijn deze: Oa, OB En OC.

3.- Kies een homotecia -verhouding die een positief getal is, bijvoorbeeld in het geval van figuur 2 is het gekozen R = 0.5.

4.- Vectoren zijn getekend Oa ', Ob ' En Oc ', die respectievelijk zijn Oa '= r ∙ OA, Ob '= r ∙ OB En Oc '= r ∙ OC. Als R Het is een positief getal, dan de vectoren Oa ', Ob ' En Oc ' Ze hebben hetzelfde adres als Oa, OB En OC. De lengte van Oa ', OB' En Oc ' Ze zijn de helft dat hun tegenhangers Oa, OB En OC, Omdat de reden is R = 0.5.

5.- Eindelijk zijn de a'b'c 'hoekpunten samengevoegd om de homothetische driehoek te verkrijgen om met reden 1/2 te abc.

Kan u van dienst zijn: vierhoekig: elementen, eigenschappen, classificatie, voorbeelden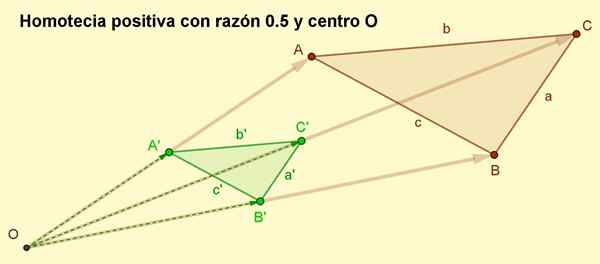 Figuur 2. Positieve Homotecia Rechts 0,5 van de ABC -driehoeksresultaten. In positieve homotecia wordt de oriëntatie gehandhaafd. (Voorbereid door: f. Zapata)

Homotecia -voorbeelden

Homotecia verschijnt in verschillende situaties:

Filmprojectoren

In een filmprojector wordt de afbeelding die in een frame is opgenomen geprojecteerd en breidt het op een scherm uit, en om de projectie rechts te zien is, is het noodzakelijk dat het frame wordt geïnvesteerd, omdat het Homotecia -centrum zich in het midden van de lens van de lens bevindt Lens van de lens van de projector, tussen het frame en het scherm (negatieve homotecia, zie figuur 3)

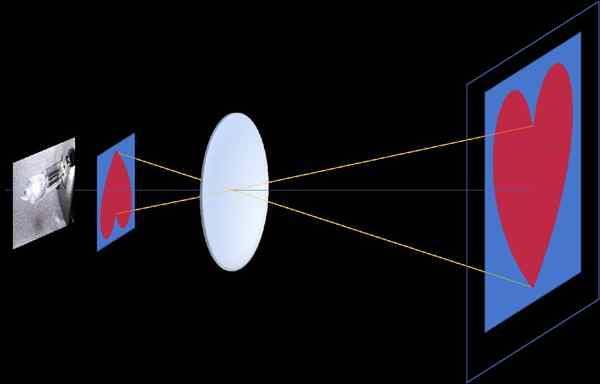figuur 3. Negatieve homotecia verschijnt in de filmprojector, tussen de afbeelding opgenomen op een doorschijnende frame en de afbeelding die op het scherm wordt geprojecteerd. Het Homotecia Center bevindt zich in het optische centrum van de lens, op zijn beurt tussen het frame en het scherm. Bron: f. Zapata.

Fotocamera's

Dit principe is ook van toepassing op de camera's: het licht van de afbeelding op een bepaalde afstand van de lens wordt geprojecteerd op de fotografische sensor, die een lichtgevoelige chemische film of een CCD -sensor kan zijn, als het een digitale camera is.

De afbeelding die in de sensor is vastgelegd, is omgekeerd ten opzichte van de echte en is meestal evenredig minder dan zij.

Praktische toepassing

De zon moet niet direct kijken, omdat het permanente schade aan het netvlies veroorzaakt, maar er zijn twee mogelijkheden om het te bestuderen: gebruik filters die de lichtintensiteit verzwakken of zijn beeld op een scherm projecteren.

Kan u van dienst zijn: proportionele variatie

Een projectieapparaat bestaat uit een lengte buis D. Een van de uiteinden van de buis is bedekt met aluminiumfolie en boren in het midden met een pin. Het andere uiteinde, dat als een scherm zal dienen, is bedekt met doorzichtig papier, dat uienpapier of albanene -papier kan zijn (groentepapier).

Oefening

Bepaal de diameter van de zon, wetende dat de terrestrische orbitale straal in de orde is van 150 miljoen kilometer, dat de projectiebuis, zoals die getoond in figuur 4, 2,2 meter lang is en dat het geprojecteerde beeld 2, 1 is cm in diameter.

Figuur 4. In de buis om de zonneschijf te projecteren treedt een negatieve homotecia -verhouding op. Bron: f. Zapata.

Oplossing

De gegevens zijn als volgt:

  • Buislengte: d = 2,2 m
  • Sun's geprojecteerde beelddiameter: S = 2,1 cm
  • Afstand van de zonnebuis: r = 150 x 10^9 m
  • Echte zonnediameter: S = ¿?

Om de diameter van de zon te verkrijgen, wordt een evenredigheidsverhouding toegepast volgens de evenredigheid van homotecia (zie figuur 4):

De afstand tot de zon bevindt zich aan de lengte van de buis, omdat de diameter van de zon tot de diameter van de geprojecteerde afbeelding is:

(R / d) = (s / s)

Het opruimen van deze gelijkheid dat de echte diameter van de zon de diameter van de projectie heeft vermenigvuldigd met het quotiënt tussen de afstand tot de zon en de lengte van de buis:

S = S (R / D)

Het plaatsen van de numerieke waarden zijn:

S = 2,1 x 10-2 M (150 x 109 m / 2.2 m)

S = 1,43 x 109 M.

Dit resultaat wordt als volgt geïnterpreteerd: de echte diameter van de zon is 1,43 miljoen kilometer.

Referenties

  1. Álvaro Rendón,. R. 2004. Technische tekening: activiteiten notebook.
  2. Antonio Álvarez de la Rosa, J. L. 2002. Affiniteit, homologie en homotecia.
  3. Baer, ​​r. 2012. Lineaire algebra en projectieve geometrie. COUER CORPORATION.
  4. Hebert, en. 1980. Algemene wiskunde, waarschijnlijkheden en statistieken.
  5. Messerve, b. EN. 2014. Fundamentele concepten van geometrie. COUER CORPORATION