Hypercubo -definitie, dimensies, coördinaten, ontvouwden zich

A hypercubo is een dimensie kubus n. Het specifieke geval van dimensie hypercubo wordt genoemd Testeract. Een hypercubo of n-cubo bestaat uit rechte segmenten, allemaal van dezelfde lengte die orthogonaal zijn in hun hoekpunten.

Mensen zien de drie -dimensionale ruimte: breed, hoog en diepte, maar het is niet mogelijk voor ons om een ​​hypercubo van dimensie groter dan 3 te visualiseren. 

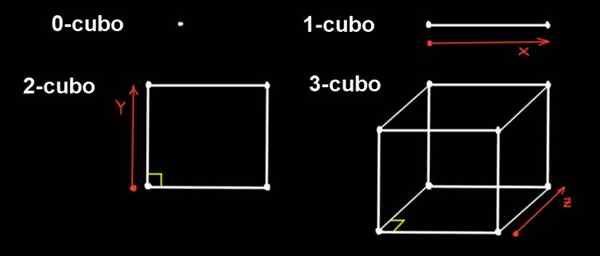
Figuur 1. Een 0-Cubo is een punt, als dat punt zich in één richting op een afstand op een 1-kubo-manier uitstrekt, als die 1-kubo een afstand uitstrekt tot in de orthogonale richting, is er een 2-cubo (van zijkanten tot x a), Als de 2-cubo een afstand uitstrekt tot in de orthogonale richting, is er een 3-cubo. Bron: f. Zapata.

We kunnen projecties maken in de drie -dimensionale ruimte om het weer te geven, vergelijkbaar met hoe we een kubus op een vlak projecteren om het te vertegenwoordigen.

In dimensie 0 is de enige figuur het punt, dus een 0-kubo is een punt. Een 1-kubo is een recht segment, dat wordt gevormd door een punt te verplaatsen op een afstand naar een afstand naar.

Van zijn kant is een 2-kubo een vierkant. Het wordt gebouwd door de 1-kubo (het segment lang a) in de richting te verplaatsen en, die orthogonaal is voor het X-adres, een afstand van.

De 3-Cubo is de gemeenschappelijke kubus. Het is gebouwd van de vierkant die hetzelfde in de derde richting (z) verplaatst, die orthogonaal is voor de X- en Y -richtingen, een afstand naar.

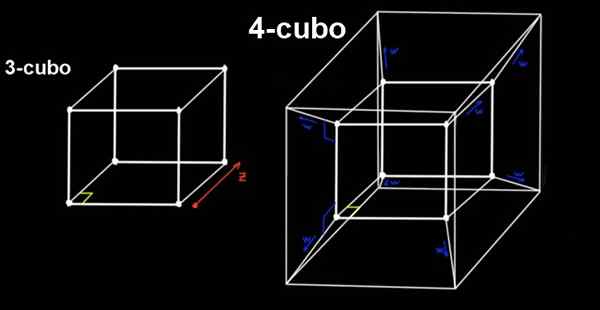Figuur 2. Een 4-cubo (testeract) is de uitbreiding van een 3-cubo in de orthogonale richting naar de drie conventionele ruimtelijke adressen. Bron: f. Zapata.

De 4-Cubo is de proef, die is gebouwd uit een 3-cubo die hetzelfde orthogonaal verplaatst, een afstand naar, naar een vierde dimensie (of vierde richting), die we niet kunnen waarnemen.

Een trigger heeft al zijn rechte hoeken, het heeft 16 hoekpunten en alle randen (18 in totaal) hebben dezelfde lengte naar.

Als de lengte van de randen van een N-Cubo of hypercubo van dimensie N 1 is, dan is het een eenheid hypercubo, waarin de langste diagonale maatregelen √n.

Kan u van dienst zijn: lineaire programmering: waar is het voor, modellen, beperkingen, toepassingenfiguur 3. Een N-Cubo wordt verkregen van een (n-1) -cubo die het orthogonaal uitstrekt in de volgende dimensie. Bron: Wikimedia Commons.

[TOC]

Wat zijn de afmetingen?

De dimensies zijn de vrijheidsgraden, of de mogelijke aanwijzingen waarin een object kan bewegen.

In dimensie 0 is er geen mogelijkheid om te bewegen en het enige mogelijke geometrische object is het punt.

Een dimensie in de Euclidische ruimte wordt weergegeven door een georiënteerde lijn of as die die dimensie definieert, de X -as genoemd. De scheiding tussen twee punten A en B is de Euclidische afstand:

D = √ [(x_naar - X_B))²]. 

In twee dimensies wordt de ruimte weergegeven door twee orthogonale georiënteerde lijnen met elkaar, genaamd X en Axis.

De positie van elk punt in deze twee -dimensionale ruimte wordt gegeven door het paar Cartesiaanse coördinaten (x, y) en de afstand tussen twee punten A en B zal elke zijn:

D = √ [(x_naar - X_B))² + (En_naar - En_B))²]

Omdat het een ruimte is waar Euclid -geometrie wordt vervuld.

De drie -dimensionale ruimte

Drie -dimensionale ruimte is de ruimte waarin we bewegen. Het heeft drie richtingen: breedte, hoog en diepte.

In een lege kamer geven de loodrechte hoeken met elkaar deze drie richtingen en aan elk kunnen we een as koppelen: X, Y, Z.

Deze ruimte is ook Euclidian en de afstand tussen twee punten A en B wordt als volgt berekend:

D = √ [(x_naar - X_B))² + (En_naar - En_B))² + (z_naar - Z_B))²]

Mensen kunnen niet meer dan drie ruimtelijke dimensies (of Euclideas) waarnemen.

Vanuit strikt wiskundige oogpunt is het echter mogelijk.

In deze ruimte heeft een punt coördinaten: (x1, x2, x3, ..., xn) en de afstand tussen twee punten is: 

D = √ [(x_1e - X_{1 B}))² + (X_2e - X_2B))² +... + (x_NA - X_NB))²].

Kan u van dienst zijn: Hypergeometrische verdeling: formules, vergelijkingen, model

De vierde dimensie en tijd

Inderdaad, in theorie van relativiteitstijd wordt tijd behandeld als nog een dimensie en een coördinaat is geassocieerd.

Maar het moet worden verduidelijkt dat deze coördinaat geassocieerd met de tijd een denkbeeldig nummer is. Daarom is de scheiding van twee punten of gebeurtenissen in de ruimte-tijd niet Euclidiana, maar volgt de metriek van Lorentz.

Een vierdimensionale hypercubo (de trigger) leeft niet in ruimte-tijd, behoort tot een vierdimensionale euclideale hyperruimte. 

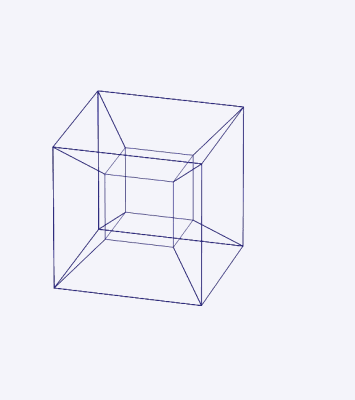
Figuur 4. 3D -projectie van een vier -dimensionale hypercubo in eenvoudige rotatie rond een vlak dat de voorste figuur naar links, terug naar rechts en van boven naar beneden verdeelt. Bron: Wikimedia Commons.

De coördinaten van een hypercubo

De coördinaten van de hoekpunten van een N-Cubo gecentreerd op de oorsprong worden bereikt door alle mogelijke permutaties van de volgende uitdrukking te maken:

(A/2) (± 1, ± 1, ± 1, .. ., ± 1)

Waar a de lengte van de rand is.

-Hij volume Van een rand van rand A is: (A/2)^N (2^N) = a^N.

-De langste diagonaal Het is de afstand tussen tegenovergestelde hoekpunten.

-De volgende zijn tegenovergestelde hoekpunten in een vierkant: (-1, -1) en (+1, +1).

-En in een Kubus: (-1, -1, -1) en (+1, +1, +1). 

-De langste diagonaal van een N-Cubo-maatregelen: 

D = √ [1 -(-1))² +… + (1 -(-1))²] = √ [n 2²] = 2√n

In dit geval werd aangenomen dat de zijde a = 2 is. Voor een N-Cubo-kant zal iedereen blijven:

d = a√n.

-Een proef heeft elk van de 16 hoekpunten verbonden met vier randen. De volgende afbeelding laat zien hoe de hoekpunten zijn verbonden in een trigger.

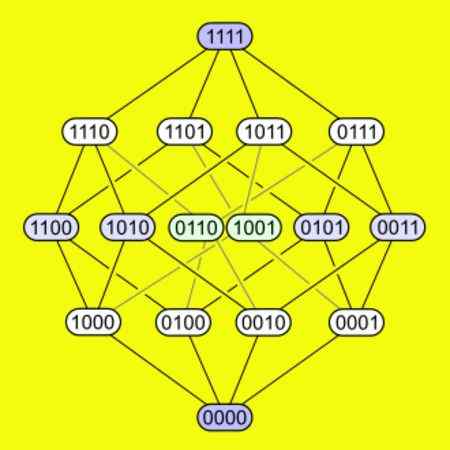Figuur 5. De 16 hoekpunten van een vier -dimensionale hypercubo worden getoond en hoe ze hetzelfde verbinden. Bron: Wikimedia Commons.

Zich afgevouwen van een hypercubo

Een regelmatige geometrische figuur, bijvoorbeeld een polyhedron, kan in verschillende figuren met een lagere dimensionaliteit worden ontvouwd.

In het geval van een 2-cubo (een vierkant) kan in vier segmenten worden ontvouwd, dat wil zeggen vier 1-cubo.

Het kan u van dienst zijn: Poisson Distributie: formules, vergelijkingen, model, eigenschappen

Evenzo kan een 3-cubo worden ontvouwd in zes 2-cubo.

Figuur 6. Een N-Cubo kan worden ontvouwd in verschillende (N-1) -kubo's. Bron: Wikimedia Commons.

Een 4-cubo (testeract) kan worden ontvouwd in acht 3-cubo.

De volgende animatie toont het ontplooien van een pens.

Figuur 7. Een 4 -dimensionale hypercubo kan worden ontvouwd in acht drie -dimensionale kubussen. Bron: Wikimedia Commons. Figuur 8. Drie -dimensionale projectie van een vier -dimensionale hypercubo die een dubbele rotatie rond twee orthogonale vlakken maakt. Bron: Wikimedia Commons.

Referenties

1. Wetenschappelijke cultuur. Hypercubo, visualisatie van de vierde dimensie. Opgehaald uit: culturracientifica.com
2. Epsilones. Tetradimensionale hypercubo of tesseract. Hersteld van: epsilones.com
3. Perez R, Aguilera A. Een methode voor het verkrijgen van een proef van de ontwikkeling van een hypercubo (4D). Hersteld van: ResearchGate.netto
4. Wikilibros. Wiskunde, polyhedra, hypercubes. Hersteld van: is.Wikibooks.borg
5. Wikipedia.  Hypercube. Opgehaald uit: in.Wikipedia.com
6. Wikipedia. Tesseract. Opgehaald uit: in.Wikipedia.com