Heptagon

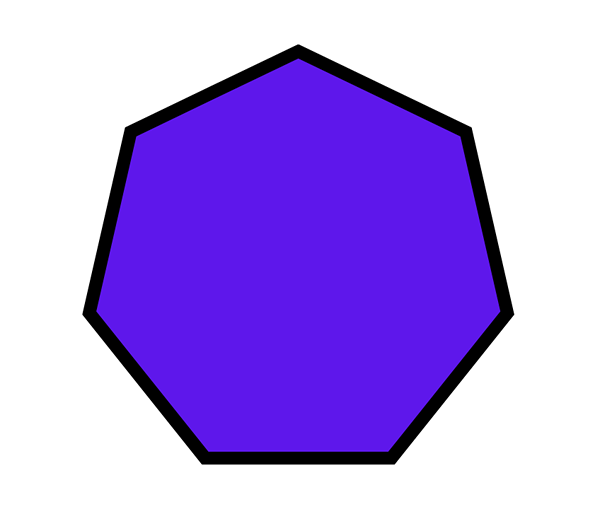
Een voorbeeld van heptagon

Wat is een heptagon?

Hij heptagon Het is een polygoon met zeven zijden en zeven interne hoeken. Als een geometrisch woord is het woord heptagon afkomstig van het Grieks Hepta, wat zeven, en gonos, vertaald als een hoek. Het is daarom een ​​polygoon met zeven hoeken.

Een polygoon is een vlakke geometrische figuur die drie of meer segmenten vormt en gesloten, ook wel genoemd zijkanten. De gemeenschappelijke punten die de zijden hebben, worden genoemd Hoekpunten.

Het gebied tussen aangrenzende zijden, aan de binnenkant van de figuur, is de Interne hoek, wiens hoekpunt ook een van de hoekpunten van de heptagon is.

Als alle kanten en interne hoeken dezelfde maat hebben, is dit een Regelmatige heptagon, anders is een onregelmatige heptagon. Onregelmatige heptons nemen een grote verscheidenheid aan vormen aan.

Een heptagon kan ook zijn convex of concaaf, Volgens de maat van zijn interne hoeken. Als de interne hoeken minder dan 180 ° meten, is de heptagon convex, maar als een of meer van de genoemde hoeken groter zijn dan 180 °, dan is het concaaf.

Een heptagon wiens zijden allemaal dezelfde maatregel zijn, wordt genoemd Balateraal. Dit kan concave of convex, regelmatig of onregelmatig zijn.

Gewone en onregelmatige heptagon

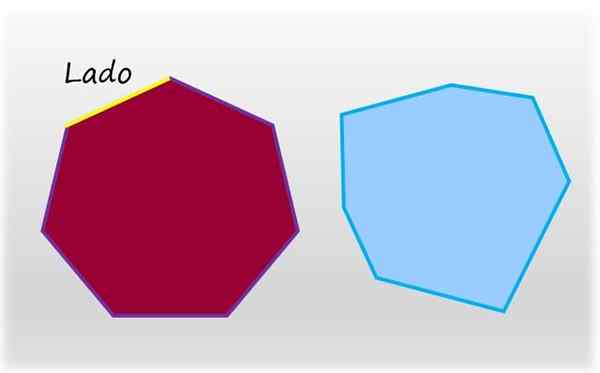De heptagon is de platte en gesloten figuur van zeven kanten. Links, een gewone heptagon, wiens zijden en interne hoeken gelijke maatregelen hebben. Aan de rechterkant, een onregelmatige heptagon. Bron: f. Zapata.

De reguliere heptagon is er een die zijn zeven zijden heeft en zijn zeven interne hoeken van gelijke maten, het tegenovergestelde van een onregelmatige heptagon, die ten minste één kant van verschillende maatregel heeft, of een andere interne hoek.

De reguliere heptagon

Symmetrie

Een gewone heptagon is een zeer symmetrische figuur. Segmenten kunnen worden getekend die een hoekpunt verbinden met het middelpunt van de andere kant, die allemaal kruisen in het midden van de heptagon. Dit zijn de zeven symmetrie -assen in de figuur.

Kan u van dienst zijn: gebied van een gewone en onregelmatige Pentagon: hoe het wordt genomen, oefeningen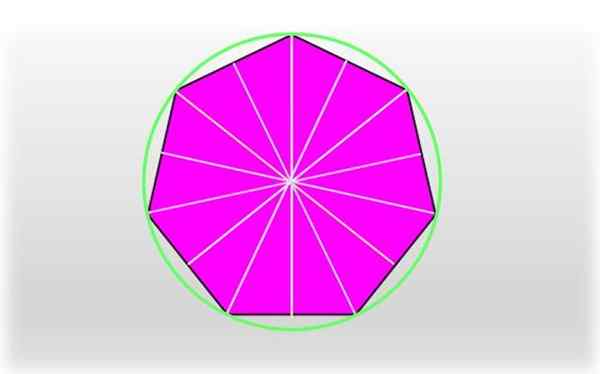 Een gewone heptagon en zijn symmetrie -assen. De omtrek die door elk van de hoekpunten van de heptagon gaat, wordt omtrek genoemd omconditiesomtrek.

Het segment dat zich bij een hoekpunt met het midden van de heptagon aansluit Circunradio, Het komt overeen met de straal van de unieke omtrek die door elk van de hoekpunten gaat, zoals getoond in de figuur.

Hoeken

In de heptagon vallen de volgende hoeken op:

• Interne hoek ϕ, wiens hoekpunt samenvalt met een van de hoekpunten van de heptagon, zijnde de zijkanten van de hoek, twee van de aangrenzende zijden van de heptagon. Voor een regelmatige heptagon is de maat van elk van de zeven interne hoeken ongeveer 128.57 °.
• Externe hoek, degene die zich vormt tussen een van de zijden en de verlenging van een van de aangrenzende zijden, het gemeenschappelijke hoekpunt tussen deze twee zijden het hoekpunt van de hoek. Evenzo worden zeven externe hoeken gevormd en wordt hun waarde berekend door 180 ° af te trekken van de interne hoek, die voor de reguliere heptagon resulteert in 51.43 °.
• Centrale hoek θ, Het heeft zijn hoekpunt in het midden van de reguliere heptgon. Het wordt berekend door 360 ° te delen door 7, wat resulteert in ongeveer 51.43 °.

De som van de interne hoek en de centrale hoek is gelijk aan 180 °, dat wil zeggen:

ϕ + θ = π

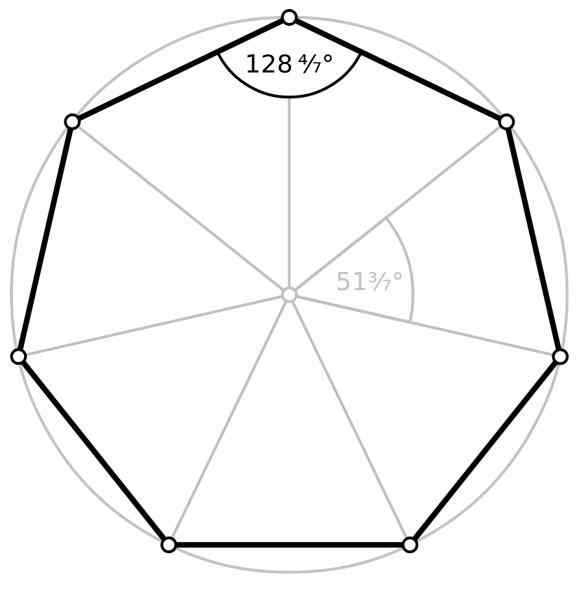Interne hoek en centrale hoek van de reguliere heptagon. Bron: Wikimedia Commons

Gebied

Voor de reguliere heptagon zijn er formules, terwijl je voor de onregelmatige heptagon je moet nemen tot andere methoden, zoals het verdelen in andere eenvoudigere polygonen, zoals driehoeken.

Het kan u van dienst zijn: regel T: kenmerken, zodat het voorbeelden zijn

Regelmatig heptagon gebied

1. Als de perimeter P en het apotheme naar_P:

Zij het voor het heptagon -gebied. Er is een formule om het gebied te berekenen, geldig voor elke gewone polygoon:

2. Als de L en Apothem bekend zijn naar_P:

Aangezien de omtrek de som van de zijkanten is en de zijde L in de reguliere heptagon meet, wordt deze verkregen:

P = 7⋅l

Vervangen in de vorige formule:

3. Als de zijkant bekend is        

Het volgende is een geschatte, geldige formule wanneer de maat van de heptagon bekend is:

A = 3.634 ∙ l²

Onregelmatig heptagon gebied

Het onregelmatige heptagongebied kan worden berekend door triangulatie, die bestaat uit het verdelen van de heptagon in vijf driehoeken (zie de volgende figuur). Het gebied van elk wordt berekend en de resultaten worden toegevoegd, waardoor het volledige gebied van de heptagon wordt verkregen.

De andere methode wordt aangeroepen Gauss -determinant, En het is noodzakelijk om de heptagon in een rechthoekig coördinatensysteem te plaatsen, om de coördinaten van elk hoekpunt te kennen. Het gebied wordt berekend door een formule die de waarden van deze coördinaten omvat.

Diagonalen

De diagonalen Het zijn segmenten die een hoekpunt verbinden met een andere die niet opeenvolgend is (als het segment twee opeenvolgende hoekpunten verbindt, is de kant)). Een heptagon heeft in totaal 14 diagonalen.

Het aantal diagonalen D van een elke polygoon, wordt berekend door de formule:

D = n · (n - 3) / 2

N = 7 vervangen, blijft:

D = 7 · (7 - 3) / 2 = 7 · (4/2) = 14

Som van interne hoeken

Voor elke heptagon, ongeacht of het al dan niet regelmatig is, is de som van zijn interne hoeken gelijk aan 900 ° of 5π radialen.

Het kan u van dienst zijn: trigonometrische redenen: voorbeelden, oefeningen en toepassingen

Deze eigenschap is heel gemakkelijk aan te tonen, hiervoor is de heptagon verdeeld in individuele driehoeken die zich niet overlappen, waarbij rechtlijnige segmenten worden getrokken die de hoekpunten verenigen, zonder elkaar over te steken.

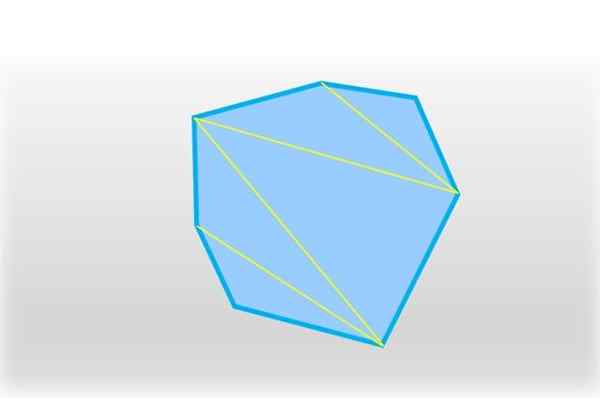Een heptagon kan worden verdeeld in vijf driehoeken, die samenvoegt door een segment twee niet -opeenvolgende hoekpunten. Bron: f. Zapata.

Vijf driehoeken worden verkregen en in elk is de som van de interne hoeken 180 °, die vermenigvuldigd met 5 gelijk is aan 900 °:

5 x 180 ° = 900 °

Formules

Omtrek

Voor een regelmatige heptagon van L wordt perimeter P als volgt berekend:

P = 7⋅l

Als de perimeter onregelmatig is, worden de lengtes van elk van de zeven zijden toegevoegd.

Interne hoekmaat

In een reguliere heptagon meet de interne hoek θ:

θ = [180 (n-2)]/n

Waar n = 7.

Apothem

Wees de zijkant van de reguliere heptagon. De apothem is het segment dat van het midden van de heptagon gaat, loodrecht op de andere kant.

Laat een_P De lengte van het apotheme. De straal van de omschreven omtrek kennen, die wordt aangeduid als r_C En de L -kant van de heptagon, je hebt:

Als je de interne hoek θ kent, is het bovenstaande gelijk aan:

Gebied

Als het een regelmatige heptagon van L is, wordt het gebied A gegeven door:

A = 3.634 ∙ l²

Wanneer de heptagon onregelmatig is, zijn de rechthoekige coördinaten van elk hoekpunt nodig, gegeven door (x_N , En_N), Waar n = 1, 2, 3 ... 7.

Vervolgens wordt de volgende formule toegepast om gebied A te vinden:

Diagonalen

Het nummer D van diagonalen wordt gegeven door:

D = n · (n - 3) / 2

Waar n = 7 voor de heptagon.

Hoe je een heptagon kunt maken

De volgende animatie laat zien hoe u ongeveer een reguliere heptagon kunt tekenen, met behulp van regel en kompas.

Constructie van de reguliere heptagon. Bron: Wikimedia Commons

Referenties

1. Alexander, D. 2013. Geometrie. 5e. Editie. Cengage leren.
2. Lemonis, m. Regelmatige hepalle -calculator. Hersteld van: calcresource.com.
3. Math Open Referentie. Polygoongebied. Hersteld van: Mathpenref.com.
4. Universe -formules. Heptagon. Hersteld van: UniversOFormulas.com.
5. Wikipedia. Heptagon. Hersteld van: is.Wikipedia.com.