Analytische meetkunde

We leggen uit welke analytische geometrie, de geschiedenis ervan, welke studies en toepassingen zijn

Wat is analytische geometrie?

De analytische meetkunde Het is de tak van wiskunde waarin geometrie en algebra worden gecombineerd, om verschillende geometrische problemen op te lossen door algebraïsche technieken.

Gebruik coördinatensystemen, zoals het Cartesiaanse coördinatensysteem, dat zijn naam René Descartes verschuldigd is. Op deze manier is het mogelijk om curven in het vlak en in de ruimte te associëren, met algebraïsche vergelijkingen.

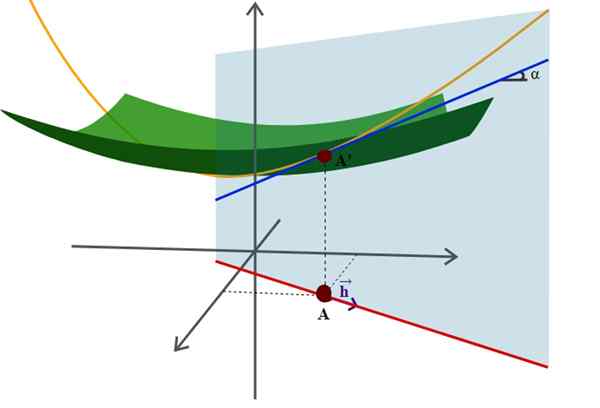
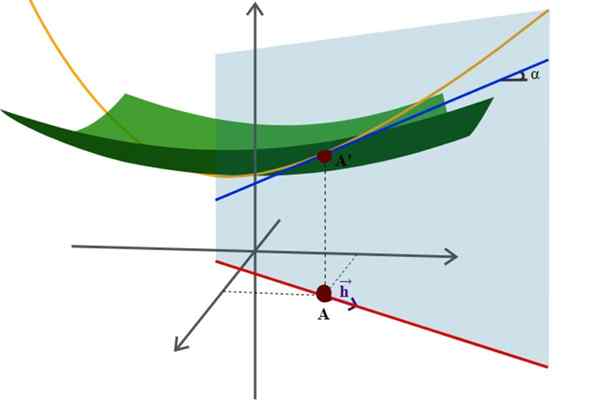Diagram van een oppervlak in de ruimte en zijn directionele derivaat, een van de vele meer geavanceerde toepassingen van analytische geometrie. Bron: Wikimedia Commons.

Een voorbeeld hiervan is de goed bekende vergelijking van de straal R -orriortie gecentreerd op de oorsprong van het coördinatensysteem:

Ongetwijfeld is het in veel gevallen eenvoudiger om te werken met de algebraïsche uitdrukking van een curve, dan met zijn geometrische weergave zelf. Dit is het geval bij het berekenen van kruispunten tussen krommen, of het vinden van raaklijnen of drooglijnen daarvoor.

Evenzo is het via analytische geometrie mogelijk om grafische afbeeldingen op te lay -outfuncties. En zoals bekend, staan ​​de functies het modelleren van wetenschaps- en engineeringproblemen mogelijk. Daarom is analytische geometrie aanwezig in de curricula van de carrières geassocieerd met deze kennisgebieden.

Korte geschiedenis van analytische geometrie

Analytische geometrie heeft zijn oorsprong in de eerste helft van de 17e eeuw, door de hand van twee opmerkelijke Franse wiskundigen: René Descartes (1596-1650) en Pierre de Fermat (1601-1665).

Rene Descartes

Men kan echter gezegd worden dat zijn achtergronddatum eeuwen de Griekse wiskundige Apollonius van Pergamo (262-190 a.C.)). Hij schreef een verhandeling over de Conics, waaraan hij hun namen verleende: omtrek, ellips, gelijkenis en hyperbool.

Het kan u van dienst zijn: samengestelde evenredigheid: uitleg, drie samengestelde regel, oefeningen

Het werk van Apollonio was dus de basis voor, veel later, de Franse René Descartes en Pierre de Fermat lagen de fundamenten van analytische geometrie, onafhankelijk. Maar Descartes wordt beschouwd als de vader van deze wetenschap, omdat hij de eerste was die zijn werken publiceerde.

Descartes, Fermat en Euler

In de toespraak van de 1637 -methode verenigde Descartes twee disciplines die tot die tijd waren gescheiden: algebra en geometrie. In zijn werk introduceert Descartes het Cartesiaanse coördinatensysteem om punten in het vliegtuig en in de ruimte te vinden.

Het maakt ook gebruik van tweede -graden algebraïsche vergelijkingen met twee variabelen, om de conische secties te beschrijven en is toegewijd aan het oplossen van geometrische problemen met hen. Ook om een ​​groot deel van de wiskundige notatie te creëren die momenteel wordt gebruikt.

Pierre de Fermat is meer geassocieerd met optica dan met analytische geometrie, maar hun bijdragen zijn opmerkelijk.

In 1629 hervatte Fermat de conica van Apollonius van Pergamo en creëerde de technieken die de analytische geometrie vormen, zijn eigen coördinatensysteem uitvinden en het sleutelconcept duidelijk definiëren van Geometrische plek, waarmee de studie van analytische geometrie begint.

Fermat's werken zagen het licht echter pas in 1679, gepubliceerd door zijn zoon, toen de wiskundige al was overleden. Om deze reden wordt het vaderschap van analytische geometrie toegeschreven aan Descartes.

Vervolgens op de Franse wiskundigen vestigde de Zwitserse Leonardo Euler (1707-1783) de formele bases van analytische geometrie. Euler introduceerde verschillende coördinatensystemen in het vlak en de ruimte: rechthoekige, polaire en schuine coördinaten, evenals transformaties van het ene systeem naar het andere.

Kan u van dienst zijn: hoe wordt de informatie verkregen in een enquête?

In zijn werken over analytische geometrie verdiepte Euler ook de classificatie van verschillende curven, volgens de mate van de representatieve algebraïsche vergelijking (derde en vierde orde) en bestudeerden de eigenschappen intensief de vergelijkingen van de raaklijnen, de krommingen, de symmetrieën en veel meer.

Welke studies analytische geometrie?

In grote lijnen richt analytische geometrie zich op de studie van geometrische elementen, zoals punten, segmenten, lijnen, krommen, oppervlakken en volumes. Om dit te doen, zoals hierboven vermeld, stelt het algebraïsche vergelijkingen vast die deze elementen beschrijven en relateren, waardoor hun management door algebraïsche technieken kan worden.

De belangrijkste doelstellingen van analytische geometrie zijn op een zeer samenvattende manier de volgende:

1. Stel het Cartesiaanse coördinatensysteem en het polaire coördinatensysteem op om punten in het vlak te vinden, evenals de uitbreiding van de ruimte in de ruimte.
2. Teken segmenten, rechte, bochten en oppervlakken op het Cartesiaanse vlak en de ruimte.
3. Leid de vergelijkingen af ​​die analytisch een curve en de constructie ervan op het vlak en/of de ruimte beschrijven, evenals de studie van al zijn eigenschappen.
4. Classificeer curven, oppervlakken en volumes.
5. Leid fundamentele formules af om problemen op te lossen op opmerkelijke punten, rechte, plannen, hoeken, parallellisme, loodrechtheid, afstanden, kruispunten, gebieden en meer.
6. Los geometrische problemen op door de toepassing van algebraïsche methoden, waarvoor formules verwijzen naar opmerkelijke punten, vergelijkingen voor lijn, plannen, hoeken, afstand tussen punten, tussen lijnen en punten, raakpunten, droge lijnen, gebieden, gebieden, gebieden en nog veel meer.
7. Werk met vectorruimtes en producten tussen vectoren.

Afstand tussen twee punten

Als een voorbeeld van de vele toepassingen van analytische geometrie, is een van de eenvoudigste de berekening van de afstand tussen twee punten van het vlak. Zijn twee punten p₁ En P₂, van coördinaten (x₁,En₁) en (x₂,En₂) respectievelijk, de afstand d tussen hen wordt berekend door:

Kan u van dienst zijn: Trinomial

Pool coördinaten

Een vlakpunt kan worden gespecificeerd door de "R" -afstand tot de oorsprong van het coördinatensysteem, polo genoemd, en de hoek die de lijn vormt die tot het punt en de paal bevat, met de horizontale as of polaire as.

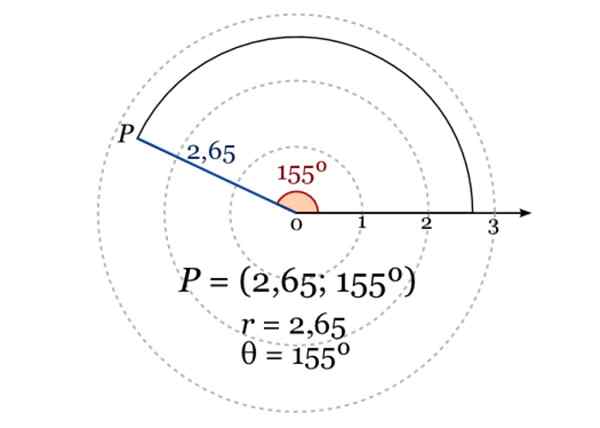De afbeelding toont de polaire coördinaten van een punt P, waarbij r = 2.65 en de hoek in graden ten opzichte van de polaire as is 155º. Bron: Wikimedia Commons.

Analytische geometrietoepassingen

Foundation of Infinitesimal berekening

Analytische geometrie is essentieel voor de ontwikkeling van oneindige berekening, omdat het de grafische weergave van curven en functies vergemakkelijkt en ermee op een analytische manier werkt, om modellen te maken die fenomenen van de natuur vertegenwoordigen.

Kaarten

Het Cartesiaanse coördinatensysteem helpt om kaarten te maken en plaatsen te identificeren door breedtegraad en lengte, gelijk aan de Cartesiaanse coördinaten van een punt in het vlak.

Topografische berekeningen

Verschillende soorten coördinatensystemen worden gebruikt in topografie en vormen de basis van hun studie en toepassingen. Onder hen is het hierboven beschreven polaire coördinatensysteem.

Celestial Bodies Trajecten

De conische secties, beschreven door analytische geometrie, nemen deel aan belangrijke natuurverschijnselen, zoals de trajecten van hemellichamen, onderworpen aan de zwaartekracht. De planeten en sommige kometen beschrijven bijvoorbeeld elliptische trajecten rond de zon, met deze in een van de schijnwerpers.

Burgerlijke architectuur en constructies

Talrijke curven maken deel uit van de architecturale constructies, bijvoorbeeld de kabels van een hangende brug kunnen de vorm aannemen van gelijkenissen.

Globale positioneringssystemen

Het Global Positioning System of GPS maakt mogelijk locaties met precisie, evenals bewegende objecten, zoals voertuigen en boten. Het helpt mensen ook gemakkelijker naar hun bestemmingen te komen en hen op de beste routes te begeleiden.