Basic trigonometrische functies, in het Cartesiaanse vlak, voorbeelden, oefening

De trigonometrische functies Van de reële variabele komen ze overeen met elke hoek (uitgedrukt in radianen), een trigonometrische reden, die sinus, cosinus, raaklijn, cotangent, secant en oogst kan zijn.

Op deze manier hebben we de zes trigonometrische functies: sinus, cosinus, raaklijn, oogstster, drogen en cotangent.

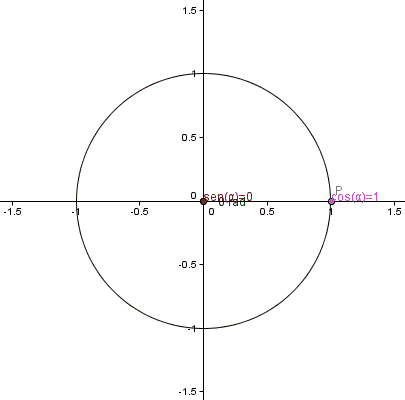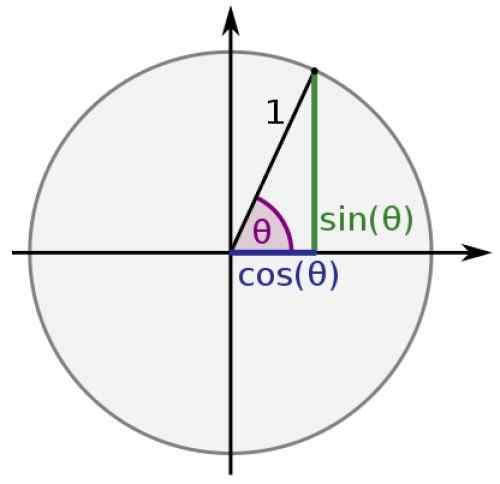
Figuur 1. Trigonometrische cirkelanimatie. Bron: Wikimedia Commons.

De trigonometrische functies voor hoeken tussen 0 en 2π worden gedefinieerd met behulp van de unitaire omtrek, van radio 1 en waarvan het centrum samenvalt met die van de oorsprong van het Cartesiaanse coördinatensysteem: het punt (0.0).

We kunnen elk punt P van coördinaten (x, y) op deze omtrek vinden.

Het segment dat de oorsprong verenigt met P, samen met de respectieve segmenten die de projecties van P op de coördinaatassen verenigen, vormen een rechthoekige driehoek, waarvan de trigonometrische redenen bekend staan ​​als de quotiënten tussen de zijkanten van de driehoek. Dus:

• sin θ = tegenovergestelde /hypotenusa cateto
• cos θ = aangrenzende /hypotenusa cateto
• tg θ = tegenover Cateto /aangrenzende cateto

En nu de redenen die het omgekeerde van het bovenstaande zijn:

• Sec θ = hypotenuse /aangrenzende cateto
• Schade θ = hypotenusa /cateto tegenover
• ctg θ = aangrenzende cateto /tegenovergestelde cateto

In de eenheidscirkel is de hypotenusa van elke driehoek gelijk aan 1 en de categorieën zijn X en Y waard: dan:

sin θ = y

cos θ = x

Figuur 2. De rechter driehoek in de eenheidscirkel. Bron: Wikimedia Commons.

Op deze manier verwerven de sinus- en cosinusfuncties altijd waarden tussen -1 en 1, terwijl de resterende:

tg θ = y/x

schade θ = 1/y

Sec θ = 1/x

Ze zijn niet gedefinieerd wanneer X of En Ze zijn 0 waard.

[TOC]

Trigonometrische functies in het Cartesiaanse vlak

Zoals we hieronder zullen zien, worden trigonometrische functies gekenmerkt door periodiek te zijn. Daarom zijn ze niet bijectief, behalve in een beperkt domein.

Functie f (x) = sin x

Beginnend in de trigonometrische cirkel op punt P (1.0), is de hoek 0 radialen. Dan roteert de straal in anti -horaire zin en groeit de sen x -functie geleidelijk totdat deze π/2 radialen bereikt (90º), equivalent aan 1.Ongeveer 571 radialen.

Kan u van dienst zijn: aanvullende hoeken: wat zijn, berekening, voorbeelden, oefeningen

Daar bereikt het de waarde y = 1 en dan neemt het af totdat het nul bereikt in π radianen (180 °). Vervolgens neemt het nog meer af, omdat de waarde negatief wordt tot het bereikt −1 wanneer de hoek 3π/2 radialen is (270 °).

Eindelijk neemt het weer toe totdat het terugkeert naar nul in 360 °, waar alles weer begint. Dit maakt y = sin x a periodieke functie van periode 2π, dus de sinusfunctie is niet bijectief.

Bovendien is de grafiek symmetrisch ten opzichte van het punt (0,0), daarom is de functie oneven.

Dan de grafiek van y = sen x:

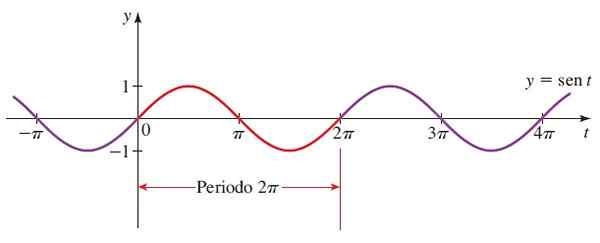figuur 3. Functiegrafiek f (x) = sin x. Bron: Stewart, J. Precculment: wiskunde voor de universiteit.

De rode sectie is de eerste periode. Negatieve hoeken worden ook overwogen, omdat de straal van de trigonometrische cirkel in een schema kan roteren.

Sen X -domein = Alle reales.

Sen x bereik of route = [-1,1]

Functie f (x) = cos x

Op punt P (1.0) is de Coseno -functie 1 waard en neemt vanaf daar af, bereikt 0 wanneer de hoek π/2 is. Blijf afnemen en neemt negatieve waarden, tot het bereiken van -1 bij hoek π.

Dan begint het geleidelijk toe te nemen totdat het 0 in 3π/2 bereikt en opnieuw waarde krijgt wanneer de straal een volledige beurt heeft geworden. Van daaruit wordt de cyclus herhaald, omdat cos x periodiek is en ook koppel is (symmetrisch rond de verticale as).

De vorm van de cosinusfunctie is dezelfde als die van de sinusfunctie, tenzij ze zijn verplaatst π/2 één ten opzichte van de andere.

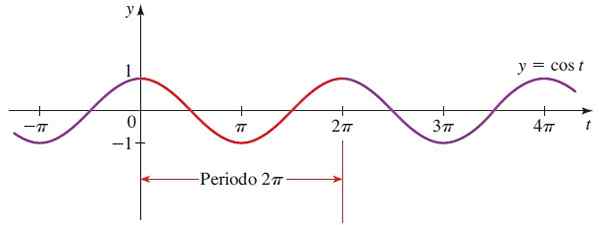Figuur 4. Functiegrafiek f (x) = sin x. Bron: Stewart, J. Precculment: wiskunde voor de universiteit.

Cos x domein = Alle reales.

Kan u van dienst zijn: punctuele schatting

Bereik of cos x route = [-1,1]

Discontinue trigonometrische functies

De functies TG X, CTG X, SEC X en Hars. Omdat deze in sommige hoeken de moeite waard zijn, maken ze, wanneer ze in de noemer verschijnen, de functie discontinu.

En omdat sinus en cosinus periodieke functies zijn, zijn de functies Tg X, Ctg X, Sec X, Harm X ook.

Tangens functie f (x) = tg x

Voor de tangensfunctie zijn de discontinuïteitwaarden: ± π/2, ± 3π/2, ± 5π/2 ... Daar duurt de functie zeer grote of zeer kleine waarden. Over het algemeen gebeurt dit voor alle veelvouden van π van de vorm (2n+1) π/2, zowel positief als negatief, met n = 0, 1, 2 ..

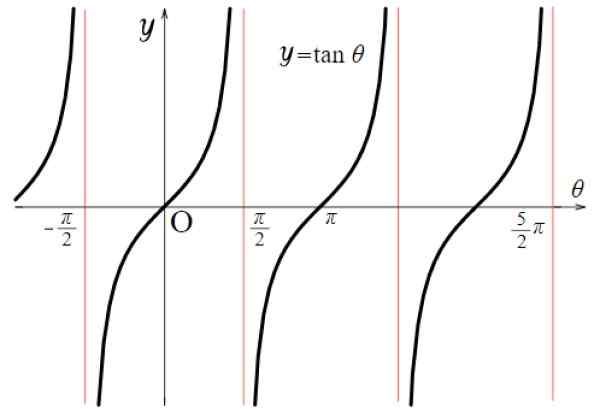Figuur 5. Functiegrafiek f (x) = tg x. Bron: Wikimedia Commons.

Daarom:

TG X -domein: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

Rang of TG X Tour: Alle reales.

Merk op dat de functie f (x) = tg x wordt herhaald tussen - π/2 en + π/2, daarom is de periode π. Bovendien is het symmetrisch met betrekking tot de oorsprong.

Cotangent -functie f (x) = ctg x

Voor deze functie komen discontinuïteitwaarden voor in 0, ± π, ± 2π ..., dat wil zeggen de gehele veelvouden van π.

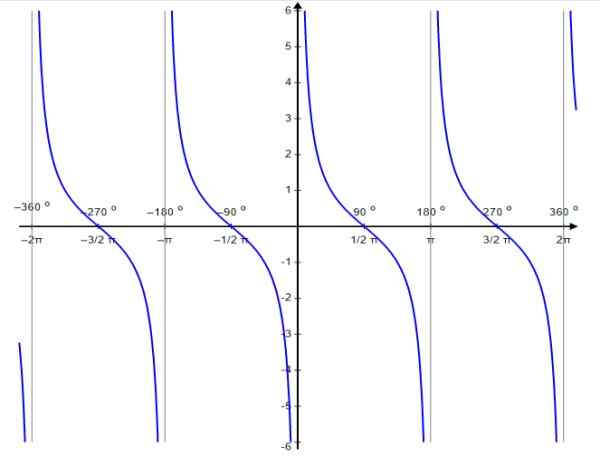Figuur 6. Functiegrafiek f (x) = cotg x. Bron: Wikimedia Commons.

Net als de tangens -functie is de cotangente functie periodieke periode π. Voor haar is het vervuld dat:

CTG X -domein: D = x ∈ R / x ≠ n π; n ∈ Z

CTG X -bereik of route: Alle reales.

Droogfunctie f (x) = sec x

De SEC X -functie heeft discontinuïteitspunten in ± π/2, ± 3π/2, ± 5π/2 ..., waarbij cos x = 0. Het is ook periodieke periode π en wordt ook waargenomen van de grafiek dat de functie nooit waarden in het interval neemt (-1,1)

Kan u van dienst zijn: hele nummers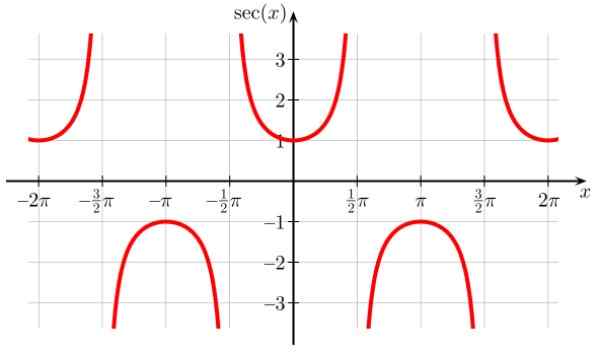 Figuur 7. Functiegrafiek f (x) = sec x. Bron: Wikimedia Commons.

Doma van Sec x: D = x ∈ R / x ≠ (2n+1) π/ 2; n ∈ Z

SEC X Bereik of route: Alle reais behalve (-1,1)

Oogstfunctie f (x) = schade x

Het is vergelijkbaar met de droogfunctie, hoewel deze naar rechts wordt verplaatst, daarom zijn de discontinuïteitspunten 0, ± π, ± 2π en alle gehele veelvouden van π. Het is ook periodiek.

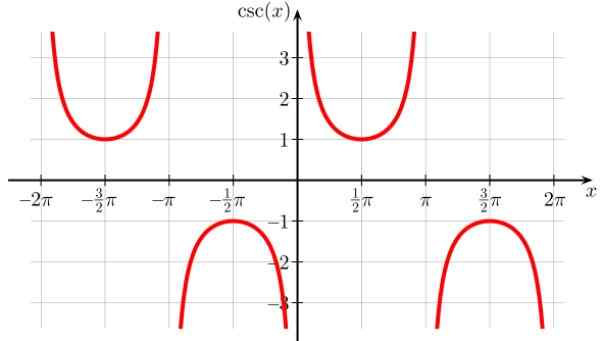Figuur 8. Functiegrafiek f (x) = schade x. Bron: Wikimedia Commons. Geek3/cc by-sa (https: // creativeCommons.Org/licenties/by-sa/4.0)

Schade domein x: D = x ∈ R / x ≠ n π; n ∈ Z

Bereik of harmonieroute: Alle reais behalve (-1,1)

Oefening opgelost

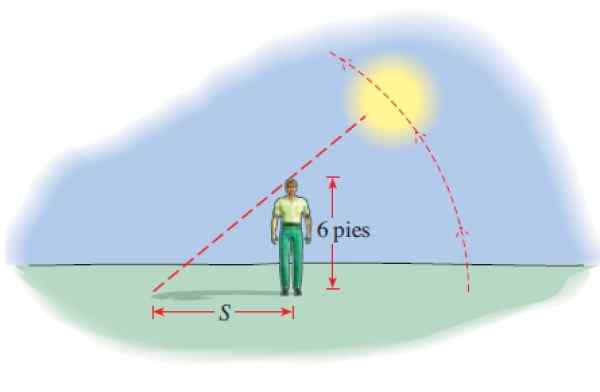
Een 6 -voet lange man projecteert een schaduw waarvan de lengte wordt gegeven door:

S (t) = 6 │cot (π.T/12) │

Met s op voeten en t het aantal uren na 6 uur 's ochtends. Hoeveel is de schaduw om 8 uur, om 12 m, om 14.00 uur en om 17:45 uur?

Oplossing

We moeten de functie voor elk van de gegeven waarden evalueren, merken op dat de absolute waarde moet nemen, omdat de lengte van de schaduw positief is:

-Om 8 uur zijn er 2 uur verstreken vanaf 6 uur, daarom is t = 2 en s (t):

S (2) = 6 │cot (π.2/12) │pies = 6 │cot (π/6) │pies = 10.39 voet.

-Wanneer het 12 n is, zijn t = 6 uur verstreken, daarom:

S (6) = 6 │cot (π.6/12) │pies = 6 │cot (π/2) │pies = 0 voet. (Op dat moment valt de zon verticaal op het hoofd van de persoon).

-Om 14.00 uur brachten ze t = 8 uur door:

S (8) = 6 │cot (π.8/12) │pies = 6 │cot (2π /3) │pies = 3.46 voet.

-Als het 17:45 uur is, zijn 11 verstreken 11.75 uur vanaf 6 uur, dan:

S (11.75) = 6 │cot (π x 11.75/12) │Pies = 91.54 voet. Op dit moment worden de schaduwen langer.

Kan de lezer de tijd berekenen waarop de schaduw van de persoon gelijk is aan zijn hoogte?

Referenties

1. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Presiversity wiskundehandleiding. Nationale Universiteit van de kust.
2. Figuera, j. 199999. Wiskunde. 1e. Diversifieerd. Bolivarian collegiale edities.
3. Hoffman, J. Selectie van wiskundeproblemen. Deel 4.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Zill, D. 1984. Algebra en trigonometrie. McGraw Hill.