Wiskundige functies

Een wiskundige functie is de relatie tussen twee magnitudes, wanneer de eerste afhankelijk is van de tweede. Luiken

Wat zijn wiskundige functies?

De Wiskundige functies Ze zijn de uitdrukking in de wiskundige taal van een relatie tussen twee variabelen, en de waarde van de eerste van de variabelen hangt af van de tweede. Normaal gesproken worden deze variabelen gesymboliseerd met de letters x en y.  Variabele X wordt domein of onafhankelijke variabele genoemd; en voor de y, codominium of afhankelijke variabele.

Laten we eens kijken naar een voorbeeld. We hebben twee variabelen of magnitudes: dollar en cent. We weten dat 100 cent gelijk is aan een dollar. Daarom is cent (x) het domein en dollar (y) komt overeen met codominium. Deze relatie kan worden uitgedrukt met de volgende functie (f):

F (x) = y / 100

Als ik 143 cent in mijn piggy bank heb en ik wil weten hoeveel dollars ik heb bespaard, pas ik de functie alleen toe:

F (x) = 143/100

Daarom heb ik $ 1,43.

We kunnen ook de omgekeerde relatie uitdrukken, dat wil zeggen dat een dollar gelijk is aan 100 cent. Bijgevolg worden de categorieën van de variabelen geïnvesteerd: dollar (x) wordt het domein terwijl cent het codominium is. We drukken het op deze manier uit:

F (x) = x x 100

Als ik $ 1,43 in mijn piggy bank heb, maar ik wil weten hoeveel cent dit cijfer gelijkwaardig is, is het voldoende om deze tweede functie toe te passen.

F (x): 1,43 x 100

Het resultaat keert terug naar mijn 143 originele cent.

De variabelen van wiskundige functies

Een variabele is gewoon een symbool (x, y, z) dat een verscheidenheid aan elementen vertegenwoordigt.

In het vorige voorbeeld symboliseerden de variabelen X en Y de dollar en de cent van de dollar. Maar dezelfde symbolen (x en y) kunnen worden gebruikt om een ​​oneindig van elementen weer te geven, zoals: leeftijd van een persoon en hun gewicht; Aantal vluchten naar een bepaalde bestemming en een periode (per week, per maand, per jaar), enz.

Kan u van dienst zijn: synthetische verdeling

De variabelen kunnen in verschillende typen worden ingedeeld, maar de meest relevante voor wiskundige functies zijn de volgende:

• Afhankelijke variabele: Degenen wiens waarde hangt af van de waarde die is toegewezen aan andere variabelen in de functie.
• Onafhankelijke variabele: Veranderingen in dit type variabele beïnvloeden de waarden van de rest van de variabelen van de functie.
• Kwantitatieve variabele: Het wordt uitgedrukt door gedefinieerde numerieke hoeveelheden. Het kunnen hele of decimale cijfers zijn.

Kenmerken van wiskundige functies

1- De relatie tussen de variabelen wordt uitgedrukt in termen van gelijkwaardigheid.

2- Voor elke waarde van variabele x is er een, en alleen een equivalent van de variabele en. En vice versa: voor een bepaalde waarde van y is er een, en alleen een resultaat van variabele x.

3- Ze kunnen grafisch worden weergegeven op een Cartesiaans vlak, waardoor het gedrag van een van de variabelen van de andere kan voorspellen.

4- De moderne definitie van wiskundige functie is te wijten aan de Duitse wiskundige Peter Dirichlet (1805-1859), die het in 1837 publiceerde.

Soorten wiskundige functies

Wiskundige functies kunnen worden geclassificeerd volgens verschillende criteria, zoals de relatie die is vastgesteld tussen de variabelen x en y o het wiskundige gedrag van de functie.

Onder de belangrijkste typen zijn de volgende:

Algebraïsche functies

Ze worden gekenmerkt door een relatie tot stand te brengen tussen componenten die worden uitgedrukt door een monomiaal of polynoom. Deze relatie kan worden bepaald door eenvoudige wiskundige bewerkingen, zoals aftrekking, vermenigvuldiging, verdeling, som, potentiëring of uitzending.

Lineaire functies

Wanneer ze op een Cartesiaans vlak worden weergegeven, verschijnen ze met de vorm van een rechte lijn die de coördinaatas op een bepaald punt snijdt. Vandaar hun naam, hoewel ze ook bekend staan ​​als first -degree functies.

Kan u van dienst zijn: gemeenschappelijke factor: kenmerken, voorbeelden, oefeningen

Functies in stukken

In dit type verandert de waarde van het codominium en verandert het gedrag van de functie. Er zijn daarom twee intervallen met ander gedrag in relatie tot de domeinwaarde.

Transcendente functies

Het zijn zeer complexe functies. Gemeenschappelijke algebraïsche bewerkingen zijn niet voldoende (aftrekking, vermenigvuldiging, verdeling, som, potentiëring of straling) om de relatie tussen de variabelen te bepalen, dus andere wiskundige hulpmiddelen moeten worden gebruikt, zoals derivaten, integralen of logaritmen.

Trigonometrische functies

Dit type functies tonen de numerieke relatie die bestaat tussen de verschillende elementen van een driehoek en andere geometrische figuren, vooral onder zijn hoeken. Formules voor de borst, cosinus, raaklijn, secant en harmonte zijn voorbeelden van dit type functies.

Injectieve functies

De functies van dit type worden gekenmerkt door de bijzonderheid van de relatie tussen domein en codominium. Met elk van de waarden van deze laatste komt slechts één domeinwaarde overeen. Het kan ook gebeuren dat een domeinwaarde geen overeenkomstige waarde in het codominium bezit.

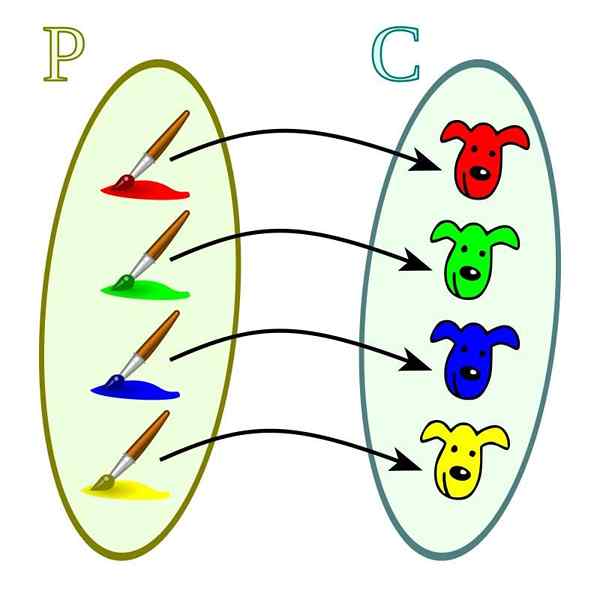Injectieffunctie. Bron: Wikimedia Commons

Onjectieve functies

In dit geval is elk van de grootten van het codominium gerelateerd aan ten minste een van de domeinwaarden. Ze onderscheiden zich van de injectieve functies waarin de codominiumwaarden kunnen worden gerelateerd aan meer dan een van de domeinwaarden.

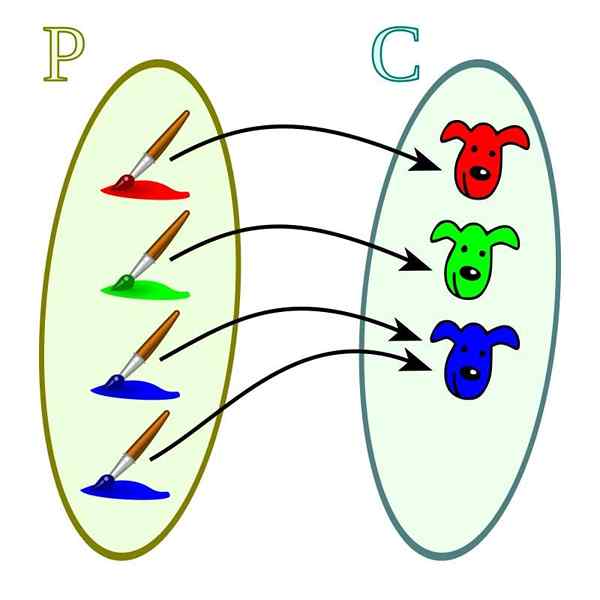Overagentieffunctie. Bron: Wikimedia Commons

Bijectieve functies

Dit type functies presenteert zowel injectieve als overjectieve eigenschappen.

Waar zijn wiskundige functies voor?

De functies worden veel gebruikt in alle wetenschappen die wiskunde hebben als een hulpwetenschap. Dit is het geval van natuurkunde, engineering, geneeskunde, financiën, statistieken, onder vele anderen.

Kan u van dienst zijn: frequentieverdeling: hoe u een tabel kunt maken, bijvoorbeeld, oefening

In het dagelijkse leven

We kunnen echter ook nuttig zijn voor het oplossen van eenvoudigere dagelijkse problemen.

Stel je voor dat je grootvader je 10 munten heeft gegeven, die je aan chocolade zult uitgeven. In de kiosk heb je de 10 munten aan de afhankelijke gegeven en hem verteld om je alle chocolaatjes te geven die met die hoeveelheid valuta kunnen worden gekocht. Ze hebben je 5 chocolaatjes gegeven. Wat is de prijs van elk?

We stellen het probleem voor: als 5 chocolaatjes gelijk zijn aan 10 munten, hoeveel munten zijn dit gelijk aan een enkele chocolade?

Onze onafhankelijke variabele (x) is de hoeveelheid chocolaatjes (5), terwijl de afhankelijke variabele (y) overeenkomt met het aantal valuta, dat wil zeggen 10.

We drukken de functie als volgt uit:

F (x) = 2x/x

F (x) = 2 (5)/5

F (x) = 10/5

F (x) = 2

En we hebben al het antwoord: elke chocolade kost 2 munten.

Referenties

1. (s/f). Elementaire functies. De site voor wiskundige functies. Uitgevoerd uit Uncations.Wolfraam.com.
2. (s/f). Wat is een functie? Uit Mathsisfun.com.