Echt reële variabele functie en de grafische weergave ervan

A Echt reële variabele functie Neem een ​​nummer dat bij de reeks reële getallen hoort en associeert het naar een andere waarde, ook echt, via een unieke correspondentieregel. Dit betekent dat het reële getal door deze regel een uniek beeld verkrijgt.

Numerieke vertrekvariabelen worden meestal aangeduid met letter X, terwijl hun afbeelding de letter is en. Aan de andere kant, aan de correspondentieregel die hen verbindt, wordt ook aangeroepen met een andere letter van het alfabet, zoals de "F" -functie, hoewel een andere kan worden gebruikt.  In compacte notatie is het geschreven:

F: x → y = f (x)

Figuur 1. Grafiek van een echte polynoomfunctie

Naar de variabele  X het heet onafhankelijke variabele, Terwijl de En Het is de afhankelijke variabele. De functie kan op verschillende manieren worden uitgedrukt, bijvoorbeeld via een wiskundige verklaring als deze:

• f (x) = 2x −3
• H (x) = −3x²
• 

Een andere vorm van expressie is via een grafiek, wat erg nuttig is omdat u hiermee het gedrag van de functie van een enkele blik kunt waarderen. Het bouwen van een grafiek is heel eenvoudig met behulp van een Cartesiaans coördinatensysteem, waarin de collega's [x, f (x)] worden weergegeven als punten in het vlak. Vervolgens voegen ze zich aan bij een zachte en continue lijn, je kunt zien hoe de functie is.

Voorbeelden

Om de grafiek te bouwen, kunt u toevlucht nemen tot een tabel met waarden waarin de te grafische punten worden geplaatst. Voor variabele X -waarden worden geselecteerd die behoren tot het domein van de functie, dat wil zeggen die wanneer vervangen in de formule, op zijn beurt reële getallen tonen.

Zodra de waarden van X zijn gekozen, worden de afbeelding y = f (x) bepaald, en op deze manier worden de puntenparen [x, f (x)] verkregen die grafisch zullen zijn.

Kan u van dienst zijn: homografische functie: hoe u kunt grafieken, opgeloste oefeningen

Er zijn enkele punten die belangrijk zijn en in de tabel moeten worden opgenomen: die waarin de grafiek naar de coördinaatassen snijdt, dat als ze bestaan, omdat niet alle functies ze kruisen.

Om ze te berekenen, ga als volgt verder:

-Kruising met de as en: x = 0 wordt gemaakt in de functieformule en de overeenkomstige waarde wordt berekend.

-Kruising met X -as: Y = 0 wordt gedaan en de vergelijking f (x) = 0 is opgelost.

Vervolgens wordt het Cartesiaanse coördinatensysteem getekend en wordt elk van de punten uitgezet, die vervolgens worden samengevoegd met een zachte en continue lijn indien mogelijk.

voorbeeld 1

Bouw een tabel met waarden en de grafiek van de volgende functie:

f (x) = x² −4

Voordat u begint, moet u het domein van de functie vinden, dat is de set van echte waarden waarvoor de functie bestaat. Omdat het een kwadratische functie is, heeft elke X -waarde die tot de reële getallen behoort een echt beeld, volgens F (x).

Vervolgens kan de tabel worden gebouwd door elke X -waarde te kiezen, en het eenvoudigste is om te beginnen met de kruispunten van de grafiek met de assen, als er zijn. Nadat ze ze hebben gevonden, worden andere punten gezocht om de tafel te voltooien.

Voor x = 0

f (0) = -4

Daarom is het eerste punt in de tabel (0, -4). Dit is de kruising van de grafiek met de as en.

Voor y = 0

Dan wordt y = 0 gedaan en de vergelijking die resultaten is opgelost:

X² −4 = 0

X² = 4

De oplossingen van deze vergelijking zijn: x₁= 2 en x₂= -2. Daarom zijn er twee kruispunten met de X -as, die de punten zijn: (−2.0) en (2.0).

Kan u van dienst zijn: perfecte cijfers: hoe u ze en voorbeelden kunt identificeren

Nu kunt u meer punten vinden om toe te voegen aan de tabel met waarden:

Voor x = 1

f (1) = (1)² - 4 = −3

Voor x = - 1

f (−1) = (−1)² - 4 = −3

Voor x =  3

f (3) = (3)² - 4 = 5

Voor x =  -3

f (−3) = (−3)² - 4 = 5

Waardetabel

De volgende tabel toont de verkregen punten, die zullen dienen om de grafiek van f (x) te bouwen:

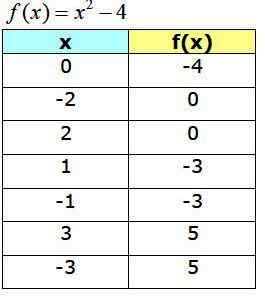Functiegrafiek f (x) = x² −4

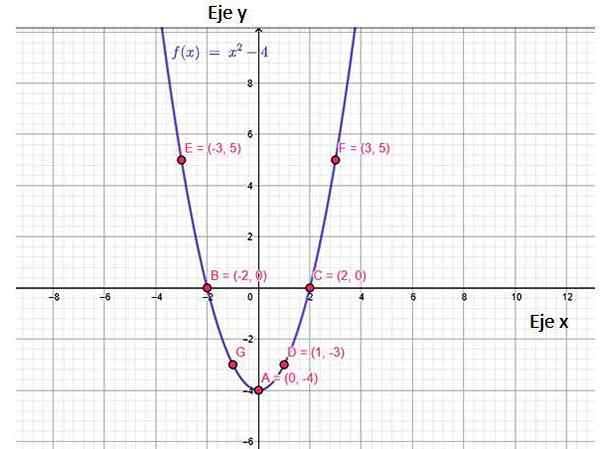Figuur 2. Functie F (x) functiegrafiek, met enkele punten die erbij horen, inclusief kruispunten met assen. Bron: f. Zapata, via Geogebra.

De grafiek van deze functie is een gelijkenis, die zich opent en op een minimumpunt heeft, genoemd hoekpunt, van coördinaten (0, −4). Het is interessant om op te merken dat de waarden van f (x) beginnen bij y = -4 tot ∞. Dit is het bereik van de functie.

Van de grafiek kan worden geconcludeerd dat de functie continu is, afneemt in het interval (−∞, 0) en van daaruit toeneemt.

Voorbeeld 2

Met de grafiek van de functie is het mogelijk om zijn domein, het bereik, de kruispunten die het heeft met de assen te kennen en het algemene gedrag te visualiseren (groei en afname).

Hieronder is de grafiek van de polynoomfunctie:

f (x) = - x⁴+4x²+1

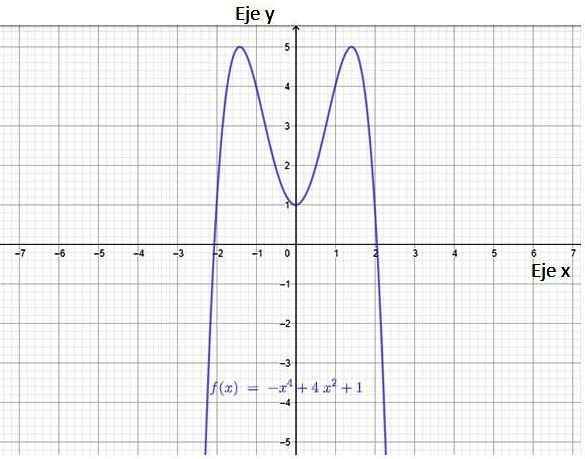figuur 3. Grafiek van een polynoomfunctie. Bron: f. Zapata door Geogebra.

Uit de afbeelding volgt dat de functie twee kruispunten heeft met de X-as, de punten (-2.0) en (2.0). Het heeft ook een kruising met de Y -as, het punt (0,1).

Het domein van een polynoomfunctie is de volledige reeks reële getallen, het wordt ook gewaarschuwd dat de functie continu is en symmetrie heeft rond de verticale as. Inderdaad kan worden geverifieerd dat deze functie is Symmetrie voor. Een functie is zelfs als deze bijeenkomt:

Kan u van dienst zijn: groene stelling, demonstratie, toepassingen en oefeningen

f (x) = f (-x)

De lezer kan verifiëren dat door -X in de functie, deze niet is gewijzigd.

Er zijn twee interessante punten, die op het hoogtepunt van y = 5 staan, zijn de maximale waarden van de functie. Het bereik van deze functie, dat wil zeggen de set waarden die de variabele neemt en, strekt zich precies uit van -∞ tot y = 5.

Om de waarden van x te kennen waarvan de afbeelding y = 5 is, wordt deze waarde vervangen in de functie:

5 = - x⁴+4x²+1

En deze vergelijking wordt verkregen:

- X⁴ + 4x² - 4 = 0

Wiens oplossingen zijn −√2 en + √2. Nou, de functie is:

-Groeien Van x -∞ tot x = −√2

-Afnemend Van x = −√2 tot x = 0

-Groeien Van x = 0 tot x = + √2

-Afnemend Vanaf x = + √2.

Oefening opgelost

Bouw de grafiek van de volgende functie:

f (x) = √ (x-5)

Oplossing

Eerst moet u het domein van de functie bepalen, om te weten welke waarden van X kunnen worden gekozen om de tabel te bouwen. In het geval van de voorgestelde functie moet de hoeveelheid binnen de wortel altijd positief of gelijk zijn aan 0, daarom:

X - 5 ≥ 0

x ≥ 5

Daarom kunnen alleen waarden groter dan of gelijk aan 5 worden gekozen voor de tabel. Wat betreft kruispunten met de coördinaatassen, de enige mogelijkheid is om y = 0 te doen, en dan x = 5.

Het is nutteloos om x = 0 te doen voor deze functie, omdat deze waarde niet tot het domein behoort.

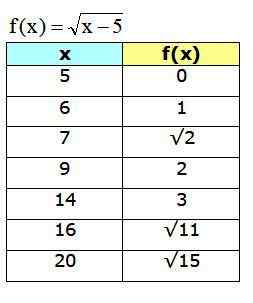
De verkregen grafiek is:

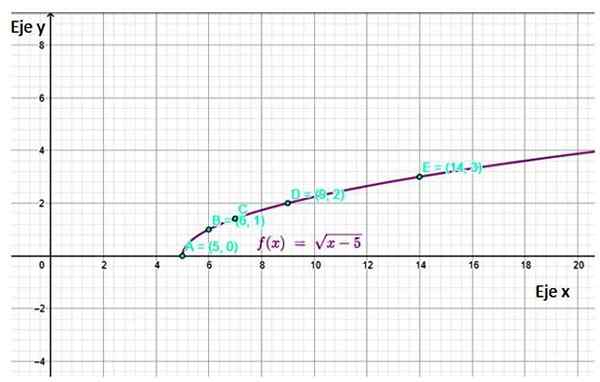Figuur 4. Functiegrafiek f (x) met enkele van de punten berekend in de tabel. Bron: f. Zapata door Geogebra.

Referenties

1. E-math zone. Soorten functies. Hersteld van: Emathzone.com.
2. Hoffman, J.G. Selectie van wiskundeproblemen. ED. SPPHINX.
3. Wiskunde is leuk. Commons functioneert referentie. Hersteld van: Mathisfun.com.
4. Eisen, b. Universe -formules. Soorten functies. Hersteld van: UniversOFormulas.com.
5. Stewart, J. 2006. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.