Homografische functie hoe te grafiek, opgeloste oefeningen

De functieHomografisch of rationeel Ón Het is een type wiskundige functie die bestaat uit de verdeling van twee polynoomcomponenten. Het gehoorzaamt de vorm P (x)/q (x), waarbij Q (x) geen nulvorm kan aannemen.

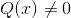
De expressie (2x - 1)/(x + 3) komt bijvoorbeeld overeen met een homografische functie met p (x) = 2x - 1 y q (x) = x + 3.

Bron: Pixabay.com

Homografische functies vormen een studiesectie van analytische functies, die worden behandeld vanuit de grafische benadering en uit het domein- en bereikonderzoek. Dit komt door de beperkingen en stichtingen die moeten worden toegepast voor hun resoluties.

[TOC]

Wat is een homografische functie?

Het zijn rationele uitdrukkingen van unieke variabele, hoewel dit niet betekent dat er geen vergelijkbare uitdrukking is voor twee of meer variabelen, waar het al in aanwezigheid van lichamen in de ruimte zou zijn die dezelfde patronen gehoorzamen als de homografische functie in het niveau.

Ze hebben in sommige gevallen echte wortels, maar het bestaan ​​van verticale en horizontale asymptoten wordt altijd gehandhaafd, evenals ook groei en verlagen intervallen. Gewoonlijk is slechts één van deze trends aanwezig, maar er zijn uitdrukkingen die in staat zijn om beide in hun ontwikkeling te tonen.

Zijn domein wordt beperkt door de wortels van de noemer, omdat er geen scheiding is tussen nul reële getallen.

Gemengde homografische functie

Ze zijn zeer frequent in de berekening, vooral differentieel en uitgebreid, noodzakelijk om onder bepaalde formules af te leiden en anti -enangel. Sommige van de meest voorkomende zijn hieronder geclassificeerd.

Nde paar homografische functie

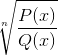
Sluit alle elementen van het domein uit die het argument negatief maken. De wortels die aanwezig zijn in elke polynoom tonen nulwaarden wanneer geëvalueerd.

Deze waarden worden geaccepteerd door de radicale, hoewel de fundamentele beperking van de homografische functie moet worden overwogen. Waar Q (x) geen nulwaarden kan ontvangen.

Kan u bedienen: transcendente functies: typen, definitie, eigenschappen, voorbeelden

Intervallenoplossingen moeten worden onderschept:

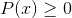
Om kruispunten te bereiken, kan de tekenmethode onder andere worden gebruikt.

Homografische functie Logaritme

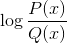
Sluit de domeinwaarden uit die negatieve intervallen en nullen gooien. Omdat de nullen al zijn uitgesloten van de noemer, de oplossingen van: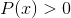

Het is ook gebruikelijk om beide uitdrukkingen in één, naast andere mogelijke combinaties te vinden.

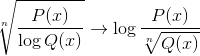
Hoe u een homografische functie kunt grafieken?

Homografische functies komen grafisch overeen met hyperbolen in het vlak. Die horizontaal en verticaal worden getransporteerd volgens de waarden die de polynomen definiëren.

Er zijn verschillende elementen die we moeten definiëren om een ​​rationele of homografische functie in te leiden.

Landgoed

De eerste zijn de wortels of nullen van de functies P en Q.

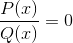
De bereikte waarden worden aangegeven op de X -as van de afbeeldingen. Het aangeven van de kruispunten van de grafiek met de as.

Verticale asymptoot

Komen overeen met verticale lijnen, die de grafiek afbakenen volgens de trends die ze presenteren. Ze raken de X -as aan in de waarden die de noemer nul maken en zullen nooit worden aangeraakt door de grafiek van de homografische functie.

Horizontale asymptoot

Weergegeven door een horizontale steeklijn, heeft een limiet afgebakend waarvoor de functie niet op het exacte punt zal worden gedefinieerd. Trends worden voor en na deze lijn waargenomen.

Om het te berekenen, moeten we hun toevlucht nemen tot een methode die vergelijkbaar is met de L'Hopital -methode, die wordt gebruikt om rationele functielimieten op te lossen die de neiging hebben om oneindig te zijn. De coëfficiënten van de hoogste bevoegdheden in de teller en de noemer van de functie moeten worden genomen.

De volgende uitdrukking heeft bijvoorbeeld een horizontale asymptoot op y = 2/1 = 2.

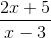
Groeiperiode

De waarden van de geordende hebben trends gemarkeerd in de grafiek vanwege de asymptoten. In het geval van groei zal de functie toenemen van waarden naarmate de elementen van het domein van links naar rechts worden geëvalueerd.

Kan u van dienst zijn: 60 delers

Afnemende interval

Geordende waarden zullen afnemen als de elementen van het domein van links naar rechts worden geëvalueerd.

De sprongen die in de waarden worden gevonden, worden niet in aanmerking genomen naarmate toeneemt of afneemt. Dit gebeurt wanneer de grafiek dicht bij een verticale of horizont staat.

Kruising met y

Nul de waarde van X maken, is de kruising met de as van de ordinaten. Dit is een zeer nuttig feit voor het verkrijgen van de grafiek van de rationele functie.

Voorbeelden

Definieer de grafiek van de volgende uitdrukkingen, vind de wortels, verticale en horizontale asymptoten, groei en verlagen intervallen en kruising met de as van de geordende.

Oefening 1

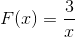
De uitdrukking mist wortels, omdat het een constante waarde heeft in de teller. De te solliciteren beperking zal zijn x anders dan nul. Met horizontale asymptoot op y = 0 en asymptote verticaal bij x = 0. Er zijn geen kruispunten met de as en.

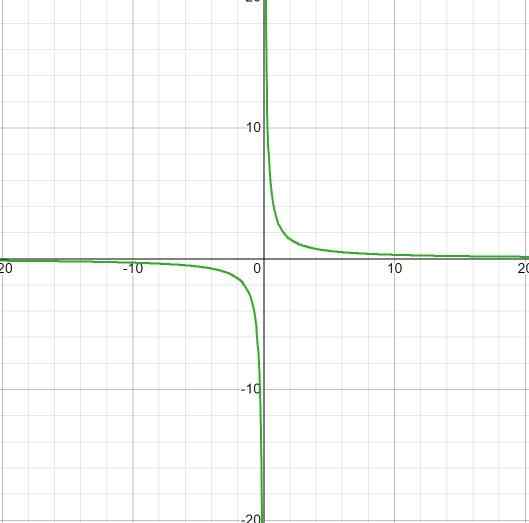
Opgemerkt wordt dat er geen groeiparen zijn, zelfs met de sprong van minder naar meer oneindig in x = 0.

Het afname -interval is

Id: (-∞; o) u (0, ∞)

Oefening 1.2

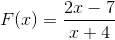
2 polynomen worden waargenomen zoals in de eerste definitie, dus gaan we verder volgens de gevestigde stappen.

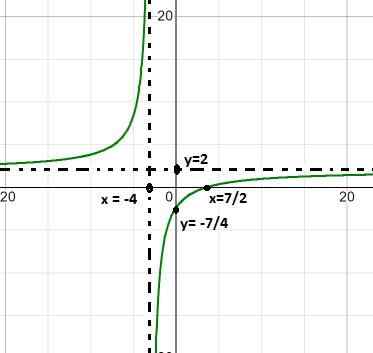
De gevonden root is x = 7/2 die het gevolg is van het gelijkmaken van de functie.

De verticale asymptoot is op x = - 4, wat de waarde is uitgesloten van het domein vanwege de rationele functieconditie.

De horizontale asymptoot is in y = 2, dit na het delen van 2/1, de coëfficiënten van de graad 1 -variabelen.

Het heeft een kruising met die besteld op y = - 7/4. Waarde gevonden na het egaliseren van de X aan nul.

Het kan u van dienst zijn: fractie gelijk aan 3/5 (oplossing en uitleg)

De functie groeit constant, met een sprong van meer naar minder oneindig rond de wortel x = -4.

Het groei -interval is (-∞, - 4) u ( - 4, ∞).

Wanneer de waarde van X bijna minder oneindig is, neemt de functie waarden in de buurt van 2. Hetzelfde gebeurt wanneer de X meer oneindig nadert.

De expressie nadert meer oneindig wanneer geëvalueerd in - 4 aan de linkerkant, en minder oneindig wanneer geëvalueerd in - 4 aan de rechterkant.

Oefening 2

De grafiek van de volgende homografische functie wordt waargenomen:

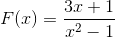
Beschrijf hun gedrag, wortels, verticale en horizontale asymptoten, groei en verminder intervallen en kruising met de geordende as.

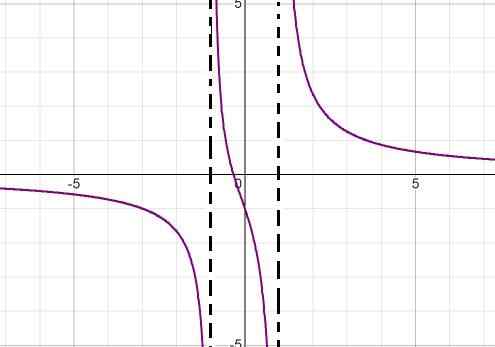
De expressie -noemer geeft aan door het verschil van vierkanten (x + 1) (x - 1) de waarden van de wortels te factureren. Op deze manier kunnen beide verticale asymptoten worden gedefinieerd als:

x = -1 en x = 1

De horizontale asymptoot komt overeen met de as van de abscis, omdat de belangrijkste kracht in de noemer is.

De enige wortel wordt gedefinieerd door x = -1/3.

De uitdrukking neemt altijd af van links naar rechts. Het nadert nul als het de neiging heeft om oneindig te zijn. Minder oneindig bij het naderen van -1 aan de linkerkant. Meer oneindig bij het naderen van -1 aan de rechterkant. Minder oneindig bij het naderen van 1 aan de linkerkant en meer oneindig bij het naderen van 1 aan de rechterkant.

Referenties

1. Benadering met rationele functies. Donald J. Nieuwe man. American Mathematical Soc., 31 december. 1979
2. Orthogonale beoordelingsfuncties. Universiteit van La Laguna Tenerife Adhemar Bultheel, Adhemar Bultheel, Pablo Gonzalez-Vera, Erik Hendriksen, Olav Njstad. Cambridge University Press, 13 feb. 199999
3. Beoordeling van benadering van echte functies. P. P. Petrushev, Vasil Atanasov Popov. Cambridge University Press, 3 maart. 2011
4. Algebraïsche functies. Gilbert Ames Bliss. Couer Corporation, 1 januari. 2004
5. Spaans Mathematical Society Magazine, 5-6 delen. Spaanse wiskundige samenleving, Madrid 1916