Spreiding van functiekenmerken, voorbeelden, oefeningen

De gespreide functie y = s (x) is een functie gedefinieerd in stukken of door delen, zodat het in een eindig interval [a, b] een eindig aantal discontinuïteiten heeft, die we zullen noemen x₀ < x₁ < x₂ <… . x_N.  In elk open interval (x_Je , X_I+1), en heeft een constante waarde van waarde S_Je, Met discontinuïteiten -Saltos- op punten x_Je.

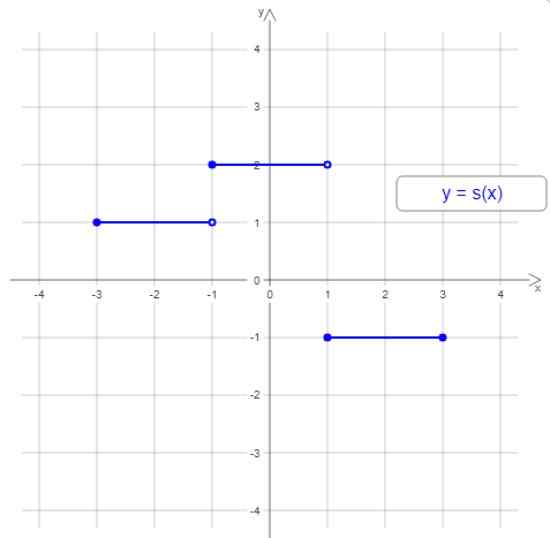
De grafiek die het gevolg is van een dergelijke functie bestaat uit stappen of stappen. Laten we hieronder een voorbeeld bekijken:

Figuur 1. Voorbeeld van gespreide functie. Bron: Wikimedia Commons.

De grafiek van deze gestimuleerde functie heeft drie stappen of gespreide intervallen, maar in het algemeen kan de gespreide functie enige stappen hebben. De breedte van de stappen kan anders zijn en de trap is niet altijd opstaan ​​of dalen.

De gespreide functie van het voorbeeld kan worden geschreven om de breedte en hoog van elke stap te specificeren, zoals deze:

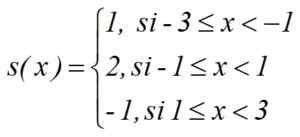
[TOC]

Kenmerken van de getrapte functie

-De functie ontvangt zijn naam door de grafiek in de vorm van stappen, gegeven door de segmenten die deze samenstellen. Elk segment heeft een deel van het domein van de functie en bij elk is de functie constant.

-Het domein van een gespreide functie zijn de waarden die behoren tot het interval waarvoor het wordt gedefinieerd: [a, b], terwijl het bereik wordt gevormd door de waarden s_Je van de hoogten van de stappen.

In het voorbeeld van figuur 1 is het domein het interval [-3,3] en het bereik is de waarden -1, 1 en 2.

-De gespreide functie is continu behalve in de waarden die elke stap afbakenen, de punten x_Je.

-Escalonada -functies kunnen worden toegevoegd en vermenigvuldigd om te leiden tot nieuwe getrapte functies.

-Zijn afgeleide is 0 voor de punten waar het wordt gedefinieerd, omdat de functie daarin constant is. Van zijn kant bestaat het afgeleide niet in discontinuïteiten.

-De integraal van de getrapte functie s (x) tussen naar En B Het bestaat en komt overeen met de som van de gebieden van de rechthoeken van breedte x_Je- X_I-1 en hoogte s_k, gelijk aan de stap.

Kan u van dienst zijn: onafhankelijke gebeurtenissen: demonstratie, voorbeelden, oefeningen

Aangezien het gebied van een rechthoek het product van de basis is op hoogte, moeten we:

Voorbeelden van gespreide functies

Binnen de gespreide functies zijn er verschillende soorten, bijvoorbeeld de functies van hele deel en de functie Eenheidsstap, evenals verschillende gespreide functies die gemeenschappelijke situaties beschrijven, zoals tarieven van veel diensten. Laten we eens kijken naar enkele voorbeelden:

- Voorbeeld 1: de hele partijen

De hele deelfunctie gebruikt vaak dubbele beugel:

f (x) = [[x]]

En het wordt gedefinieerd als een functie die aan elk reëel getal het dichtstbijzijnde of kleinere geheel getal toewijst, waarbij elk decimaal dat het nummer heeft negeren. Naarmate het geval kan zijn, hebben we:

Dak- of luchtfunctie

Wijst aan elke domeinwaarde het dichtstbijzijnde gehele getal door overtollig. Bijvoorbeeld:

[[+2.56]] = 3

Het decimale deel dat 0 is, wordt genegeerd.56 en het dichtstbijzijnde geheel getal is toegewezen dat groter is dan 2.

Een ander voorbeeld:

[[-4.2]]= -3

Nogmaals, het decimale deel 0 is weggelaten.2 en het hoogste grootste gehele getal dichter bij -4 wordt beschouwd als een waarde van de functie, die -3 is.

Merk in de volgende figuur de grafiek van de plafondfunctie op dat de stap wordt afgebakend door een kleine holle cirkel links en één volledig rechts, omdat een willekeurig aantal van het interval, het grootste geheel getal wordt toegewezen tussen de uiteinden tussen de uiteinden tussen de uiteinden tussen de uiteinden tussen de uiteinden eindigt tussen de uiteinden van het interval.

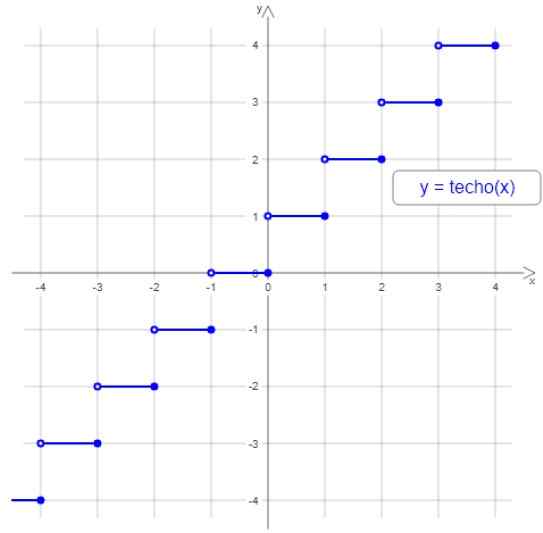Figuur 2. Het dak- of luchtfunctie. Bron: Wikimedia Commons.

Alle waarden tussen 3 en 4 worden bijvoorbeeld toegewezen aan de gehele 4, die tussen -2 en -1 liggen, worden de -1 enzovoort toegewezen.

Vloer- of grondfunctie

Wijst standaard aan elke domeinwaarde het dichtstbijzijnde gehele getal toe. Voorbeelden van deze functie zijn:

Kan u van dienst zijn: hoeveel tienden zijn er in een eenheid?

[[+3.7]] = 3

[[-1.5]] = -2

[[π]] = 3

Beide functies zijn continu behalve voor hele getallen, waar sprongen worden gepresenteerd, en het is constant voor de waarden tussen de gehele getallen k en k+1.

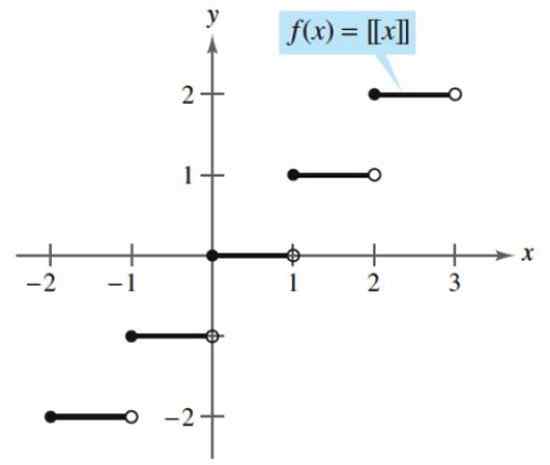figuur 3. Vloer- of grondfunctie. Bron: Larson, r. Berekening van een variabele.

- Voorbeeld 2

In een stad is het taxistarief 3.$ 65, voor de eerste 100 m. En voor elke 100 m zijn 0.$ 18, is de limiet per route van 50 km.

Het is gewenst om de functie vast te stellen die de route in meters relateert met de kosten van de service met $, die dit formulier moeten hebben:

f (x) = 3.65 + 0.18. [[X /100]] $

Waar de hele onderdeelfunctie van de Sky -functie kan zijn, waaraan de basissnelheid die 3 is is toegevoegd.$ 65. Als we bijvoorbeeld willen weten hoeveel het wordt betaald voor een reis van 6.25 km = 6250 m, we zullen:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 15.$ 65

Als het taxi -bedrijf een vloerfunctie kiest, zou de klant iets minder betalen voor de reis:

f (x) = 3.65 + 0.18. [[x /100]] $ = 3.65 + 0.18 . [[6250/100]] $ = 3.65 + [[11.25]] $ = 14.$ 65

Opgeloste oefeningen

- Oefening 1

Oproepen op lange afstand tussen steden A en B kosten 0.40 $ 10 minuten. Na die periode is de fractie of extra minuut 0 waard.05 $.

Druk de kosten C (t) uit van een oproep die een bepaald aantal minuten duurt.

Oplossing

We kunnen deze functie uitdrukken als we analyseren wat er met elke optie gebeurt voor de duur van een oproep:

Voor t ≤ 10 minuten

Wanneer T, wat de tijd is die de oproep duurt, kleiner is dan of gelijk is aan 10 minuten, worden betaald 0.$ 40.

Kan u van dienst zijn: 2 -digitafdelingen opgelost

Daarom:

f (t) = 0.$ 40 voor T inbegrepen tussen 0 en 10 minuten.

We hebben al een deel van de functie.

Voor t> 10 minuten

Entero t Case

Laten we nu eens kijken wat er gebeurt als de tijd van t = 10 minuten wordt overschreden: het kan gebeuren dat het overtollige een geheel getal is, bijvoorbeeld dat het gesprek precies 11, 12, 13, 14 minuten of meer duurt. In dat geval zal het bedrag van de oproep zijn:

f (t) = 0.40 + 0.05 (T-10) $, voor t groter dan 10 minuten, met hele T.

Dat wil zeggen dat in dit geval: t = 11, 12, 13, 14, 15 ... minuten.

Stel bijvoorbeeld dat het gesprek precies 15 minuten duurt, de kosten zullen zijn:

F (15) = 0.40 + 0.05 (15-10) $ = 0.$ 65

Decimale zaak

Overweeg ten slotte de zaak waarin de oproep een tijdje duurt met een decimaal deel. Stel bijvoorbeeld dat de oproep 15 minuten en 45 seconden duurt, wat decimaal zou zijn 15.75 minuten.

We kunnen het uitdrukken in termen van het hele deel van het vloertype, ervan uitgaande dat het bedrijf de klant of de hemel meer voordelen wil geven:

f (t) = 0.40 + 0.05 ⋅ [[T-9]] $

Laten we eens kijken wat de klant zou betalen als het een vloerfunctie was:

F (15.75) = 0.40 + 0.05 ⋅ [[[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 6 $ = 0.$ 70.

Of als een Sky -functie, in dat geval zouden de kosten zijn:

F (15.75) = 0.40 + 0.05 [[15.75-9]] $ = 0.40 + 0.05⋅ [[6.75]] $ = 0.40 + 0.05 × 7 $ = 0.75 $.

Functie en grafisch

Als functie gedefinieerd door onderdelen is:

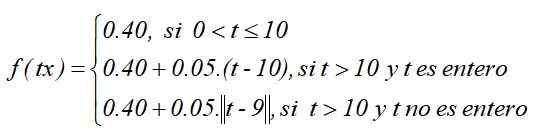
De grafiek van de functie zou zo zijn, ervan uitgaande dat de volledige functie van het plafondtype is gekozen:

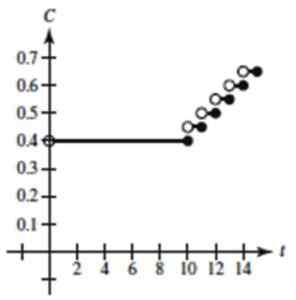Figuur 4. Grafiek van de getrapte functie van de oefening opgelost 1. Bron: Larson, r. Berekening van een variabele.

- Oefening 2

Bereken de integrale ∫s (x) dx tussen -3 en 3 van de getrapte functie:

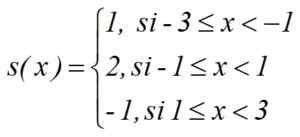
Oplossing

We passen de definitie toe voor de integrale van de gespreide functie:

Daarom is de integrale gezochte ik:

I = 1. [(-1)-(-3)] + 2.[1- (-1)]+(-1).[3-1] = 2+4-2 = 4

Referenties

1. Jiménez, r. 2006.Wiskundige functies. Pearson Education.
2. Larson, r. 2010. Berekening van een variabele. 9NA. Editie. McGraw Hill.
3. Wiskunde IV. Functie. Hersteld van: cobaqroo.Edu.mx.
4. Wikipedia. Hele onderdeel functioneert. Hersteld van: is.Wikipedia.borg.
5. Wikipedia. Gespreide functie. Hersteld van: is.Wikipedia.borg.