Breuken typen, voorbeelden, oefeningen opgelost

De breuk of fractionele getallen Het zijn die getallen die worden weergegeven die het quotiënt tussen twee gehele getallen aangeven naar En B, zo lang als B is anders dan 0. 1/3 is bijvoorbeeld een fractie die leest als "een derde".

Naar het nummer naar Het is bekend als teller van fractie en B als noemer Van hetzelfde. De noemer geeft aan in hoeveel delen het geheel moet worden verdeeld. Van zijn kant geeft de teller aan hoeveel delen van dat geheel.

Figuur 1. Hoeveel porties heeft deze chocoladereep? Bron: PiqSels.

Het geheel is alles dat wil verdelen of fractie, bijvoorbeeld een pizza of de chocoladereep weergegeven in figuur 1. De balk is zo gemaakt dat het heel gemakkelijk is om het in 5 gelijke delen te verdelen, waarbij elk deel gelijk is aan 1/5 van de volledige balk.

In fractie of fractioneel nummer 1/5 is de teller 1 waard en de noemer is 5 waard. De fractie luidt "A Fifth".

Stel dat we 3 stukken chocolade eten. We zouden zeggen dat we 3/5 delen van de bar hebben gegeten en dat 2/5 delen overblijven om te delen met een vriend. We kunnen ook zeggen dat we "Three Fifth of Chocolate" hebben aten en "twee vijfden" aan de vriend geven.

De grafische weergave van deze fractionele getallen is als volgt:

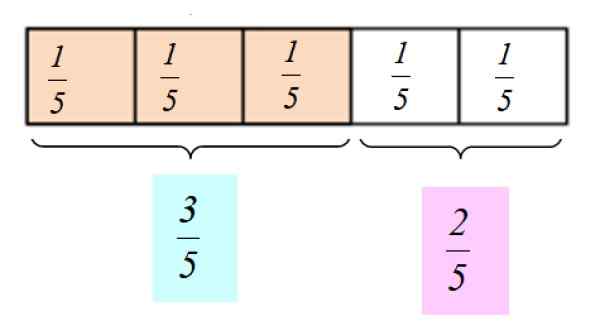Figuur 2.- Grafische weergave van breuken 3/5 en 2/5. Bron: f. Zapata.

[TOC]

Soorten breuken

Eigen breuken

Een breuk is zijn eigen wanneer de teller kleiner is dan de noemer en dus is de waarde ervan minder dan 1. De breuken van de vorige sectie, in het voorbeeld van chocolade, zijn hun eigen breuken.

Andere voorbeelden van hun eigen fracties zijn: ½; 8/10; 3/4 en meer.

figuur 3.- Zowel 1/4 als 1/2 zijn hun eigen breuken. Bron: Wikimedia Commons.

Onjuiste breuken

De teller van onjuiste breuken is groter dan de teller. Bijvoorbeeld 4/3, 8/5, 21/10 behoren tot deze categorie.

Duidelijke breuken

Deze breuken vertegenwoordigen een volledig nummer. Onder hen zijn 4/2, 10/5 en 27/3, want als we er goed uitzien, geeft het resultaat van het verdelen van teller tussen de noemer van deze breuken een geheel getal.

Dus: 4/2 = 2, 10/5 = 2 en 27/3 = 9.

Gelijkwaardige breuken

Twee breuken N/M en P/Q zijn equivalent wanneer de verdeling van de teller tussen noemer dezelfde hoeveelheid wordt verkregen. Op deze manier vertegenwoordigen de equivalente fracties hetzelfde deel van het geheel.

Als voorbeeld hebben we breuken: 15/2 en 30/4. Door 15 door 2 te delen, krijg je 7.5, maar het is ook hetzelfde als 30 wordt gedeeld door 4.

Kan u van dienst zijn: injectieve functie: waar het uit bestaat, waarvoor is het en voorbeelden

Om te weten of twee breuken N/M en P/Q gelijkwaardig zijn, wordt de naleving van de volgende gelijkheid geverifieerd:

N*q = m.P

Onherleidbare breuken

Wanneer de teller en de noemer worden verdeeld, zowel door dezelfde figuur als zolang het resultaat geheel is, wordt een breukequivalent aan het origineel verkregen, maar met kleinere getallen.

Dit proces gaat door terwijl de teller en de noemer dezelfde exacte deler hebben. Als het niet mogelijk is om door te gaan met delen, is de Onherleidbare fractie van de oorspronkelijke fractie.

Het voordeel dat moet werken met de onherleidbare fractie is dat een equivalente fractie wordt verkregen, maar met kleinere aantallen. Dat is de reden waarom wanneer u met breuken werkt, u ervoor moet zorgen dat u deze waar mogelijk kunt verminderen, om berekeningen te vergemakkelijken.

Stel dat fractie 12/20, als teller en noemerparen, beide kunnen worden gedeeld door 2:

12/20 = 6/10

En nog een keer:

6/10 = 3/5

De 3/5 fractie is gelijk aan 12/20, maar eenvoudiger.

Gemengde nummers

Een onjuiste fractie geeft ook representatie toe als een gemengd aantal, dat wordt genoemd omdat het een heel deel heeft en een ander fractioneel deel, het fractionele deel is een eigen fractie.

Laten we eens kijken naar een snel voorbeeld met fractie 15/2 waarvan we weten dat het gelijk is aan 7.5.

We kunnen als een gemengd nummer uiten tot 15/2 als dit:

15/2 = 7 + 0.5

Maar 0.5 = ½. Daarom 15/2 = 7½ die leest "zeven en een medium".

Voorbeelden van breuken

Fractionele aantallen zijn nodig omdat zowel natuurlijke als gehele getallen onvoldoende zijn wanneer we dingen zoals de chocoladereep willen verdelen.

En daarom is er een oneindige verscheidenheid aan meetpatronen en objecten waarvan de specificaties fractionele getallen omvatten, en niet te vergeten de hoeveelheid alledaagse situaties waarin deze nodig zijn.

Voedselaankopen

In landen waar het decimale metrische systeem wordt gebruikt, is het gebruik van kilo gebruikelijk om te verwijzen naar het gewicht van veel voedingsmiddelen. We willen niet altijd hele bedragen kopen, maar een beetje meer of iets minder.

Daarom vragen we:

• ½ kg vis
• ¾ kg tomaten
• ¼ kilo ui
• 1 ½ kg perziken (1 en een halve kilo).

En bij het gebruik van de Anglo -Saxon -meetpatronen gebeurt hetzelfde: we hebben 2 en een half pond of 1/4 van iets nodig.

Kan u van dienst zijn: evaluatie van functies

Al deze cijfers zijn fractioneel en, zoals we hebben gezien, komen ze overeen met twee verschillende soorten breuken: eigen en onjuist.

Keukenrecepten

Keukenrecepten maken vaak gebruik van fractionele nummers om het aantal bepaalde ingrediënten aan te geven. Bijvoorbeeld:

• ½ kopje bloem
• ¾ kg suiker om een ​​cake te bereiden.

Lengtes en diameters

Meubelsafmetingen, textielstukken en allerlei soorten huishoudelijke gebruiksvoorwerpen worden gemeten in metro- of inch fracties, of het decimale metrische maatregelen van maatregelen of Anglo -saxon worden gebruikt.

Zelfs in landen waar het decimale metrische systeem de overhand heeft, worden commercieel koper-, staal- en andere sanitaire materialen meestal geleverd met diameters die zijn gespecificeerd in inches. Evenzo, andere hardware -stukken zoals schroeven en moeren.

Als een inch is gelijk aan 2.54 cm, meestal worden deze stukken, die kleine diameters hebben, uitgedrukt in inch fracties.

Zeer veel voorkomende maatregelen voor binnenlandse pijpen zijn:

• ½ inch
• ¼ inch
• 3/8 en 5/8 inch.

Tijdslots

Dagelijks worden de fractionele getallen gebruikt om tijdsintervallen uit te drukken, zoals ¼, ½ en ¾ van een uur, of zelfs een beetje groter: 1 uur en ¼ enzovoort.

Figuur 4. Ze zijn half elf voorbij deze handklok. Bron: Pixabay.

Oefeningen met breuken

- Oefening 1

Vandaag heeft Juanito een cake op zijn verjaardag naar school gebracht en wil het onder al zijn vrienden verspreiden, maar de leraar wil een stuk geven dat drie keer groter is met betrekking tot dat van de kinderen.

Rekening houdend met dat er 24 kinderen + de leraar zijn, aan wie hij het equivalent van drie stukken wil geven, hoeveel stukken de cake moeten snijden?

Oplossing

Als Juanito de cake alleen onder zijn vrienden wilde verdelen, zou elke corresponden 1/24 corresponderen.

Maar omdat de leraar een deel wil geven en dat het stuk drie keer groter is, zou ik de cake moeten verdelen onder 24 studenten + 3 stuks voor de leraar. Dat wil zeggen, elk kind komt overeen met 1/27 stukken en de leraar 3/27 stukken.

Bovendien, als we de 3/27 fractie verminderen, krijgen we de leraar om 1/9 een deel van de taart te nemen.

- Oefening 2

Een bedrijf met een baas en drie werknemers heeft elke maand € 6000 inkomsten. Hoeveel geld komt elke persoon overeen als de baas de helft wil behouden van wat hij heeft gewonnen?

Kan u van dienst zijn: rhomboid: kenmerken, hoe u de perimeter en het gebied kunt verwijderen

Oplossing

Als de baas de helft wil winnen, moet hij bij 6000/2 blijven, wat € 3000 maakt. Van de andere resterende € 3000 is wat de drie werknemers moeten worden verdeeld. Dus elke werknemer wint 3000/3, wat resulteert in € 1000.

- Oefening 3

Vind de onherleidbare fractie van:

a) 12/18 en b) 4/11

Oplossing voor

In het eerste geval hebben we gemerkt dat zowel de teller als de noemer even zijn en deelbaar tussen 2. Ze zijn ook deelbaar tussen 3, omdat 12 en 18 veelvouden van dat figuur zijn.

Dus we kunnen de fractie vereenvoudigen door zowel de teller als de noemer te delen tussen 2 of 3, de volgorde is onverschillig.

Beginnend met delen door 2:

12/18 = 6/9

Nu merken we dat zowel de teller als de noemer van deze equivalente fractie veelvouden van 3 zijn, dus verdelen beide tussen deze figuur:

6/9 = 2/3

En omdat 2 en 3 priemgetallen zijn, hebben ze geen andere gemeenschappelijke deler meer behalve 1. We hebben de onherleidbare fractie bereikt.

De maximale gemeenschappelijke MCD -deler van de teller en de noemer had ook kunnen worden berekend. Voor 12 en 18:

MCD (12,18) = 6.

En dan worden teller en noemer gedeeld door dit nummer, wat gelijk is aan het doen in fasen.

Oplossing B

Hier zien we dat 11 een priemgetal is en de divisors zijn 1 en 11. Van zijn kant geeft 4 toe als divisors van 4, 2 en 1. Behalve 1 hebben deze cijfers geen gemeenschappelijke deler en daarom is de 4/11 fractie onherleidbaar.

- Oefening 4

Geef aan welke de grootste fractie van elk paar is:

a) ¾ en 5/4

b) 3/7 en 4/9

Oplossing voor

Wanneer twee positieve breuken dezelfde noemer hebben, is de grootste er een die de grootste teller heeft. Daarom is 5/4 groter, omdat 5> 3.

Oplossing B

Als breuken N/M en P/Q een andere noemer hebben en beide positief zijn, zijn de vergelijkingscriteria als volgt:

Zonder.Q> M. P, dan n/m> p/q

Een andere optie is om de decimale uitdrukking van elke fractie te vinden en te vergelijken.

Volgens het eerste criterium: n = 3, m = 7, p = 4, q = 9. Daarom: n.Q = 3*4 = 12 en m.P = 7*4 = 28.

Zoals 12< 28, ocurre que 3/7 < 4/9.

Of we drukken elke fractie uit als decimaal en verkrijgen dit:

3/7 = 0.428571428… .

4/9 = 0.44444444… .

De suspensieve punten geven aan dat de hoeveelheid decimalen oneindig is. Maar dit is voldoende om dat inderdaad te verifiëren, 4/9> 3/7.

Referenties

1. Baldor, een. 1986. Rekenkundig. Codex -edities en distributies.
2. Carena, m. 20199999999999999999999999999999999999999111 2019 2019 20199999 E moetene9999191999998311133113331322111152222222111231311111111111122111111111121111111111111111111111111111 -11111111111a's11111a's1a's1a's1a's1a's1a's D1a's Dam dat ’TO. Wiskundehandleiding. Nationale Universiteit van de kust.
3. Figuera, j. 20000000000000000000. Wiskunde 8. Co-bo edities.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. De wiskundepagina. Wat is een fractie? Hersteld van: themathpage.com.