Breuken gelijk aan 2/3

De breuken gelijkwaardig aan ⅔ ((Tweederde wordt gelezen) zijn degenen wiens waarde, uitgedrukt op een decimale manier, dezelfde is die wordt verkregen door 2 te delen door 3: 0.6666 ... De suspensieve punten geven aan dat 6 oneindige tijden in deze divisie verschijnen.

Een fractie -equivalent aan 2/3 is de 4/6 fractie, omdat blijkt dat na het oplossen van de verdeling tussen 4 en 6 expliciet de decimale 0.6666 .. . Dan kan worden gezegd dat 4/6 = 2/3 = 0.6666 .. .

Fracties 2/3 en 4/6 zijn equivalent omdat door het nummer van de teller te delen door de noemer hetzelfde krantennummer 0.66666 .. . (Bron: F. Zapata)

Een fractie, zoals de naam al aangeeft, is een deel of deel van de eenheid. De fractie ⅔ wordt verkregen door de eenheid in drie gelijke delen te delen en twee van die onderdelen te nemen.

Elke fractie bestaat uit een bovenste gedeelte, genaamd teller, gescheiden van de bodem of noemer, Door de breuklijn. De noemer geeft aan hoeveel delen van de eenheid is verdeeld en de teller geeft aan hoeveel van deze partijen in aanmerking moeten worden genomen.

Overweeg nu de 4/6 fractie (lees Vier zesde)). Het is bewezen dat deze fractie gelijkwaardig is aan ⅔, omdat om de eenheid in zes delen te verdelen, deze stappen moeten worden gevolgd:

1. Verdeel de eenheid in drie gelijke delen.
2. En verdeel vervolgens elk van deze delen door de helft en verkrijgt in totaal zes gelijke delen.

Als 4 delen van 1/6 van de eenheid zijn gegroepeerd, is de verkregen hoeveelheid een fractie van identieke waarde waaraan 2 delen van 1/3 van de eenheid worden verkregen. In de volgende grafiek wordt de beschreven procedure uitgevoerd: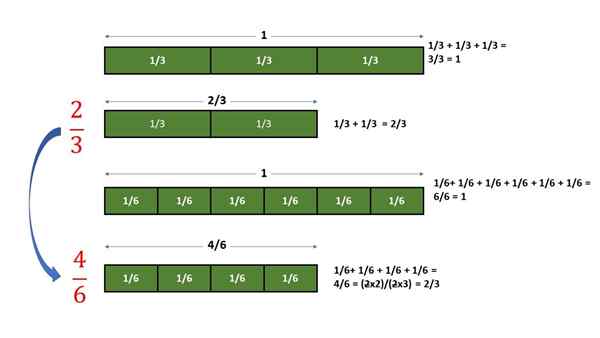

Grafische verificatie dat fractie 2/3 gelijk is aan fractie 4/6. Bron: f. Zapata.

Kan u van dienst zijn: numerieke analogieën: typen, toepassingen en oefeningen

Methoden om gelijkwaardige breuken te vinden

Merk op dat de equivalente fractie 4/6 kan worden verkregen van 2/3 door te vermenigvuldigen met zowel de teller als de noemer van deze laatste.

Wanneer tegelijkertijd de teller en de noemer van een fractie met hetzelfde getal vermenigvuldigt, wordt een equivalente fractie verkregen.

Een andere manier om een ​​fractie -equivalent aan een ander te vinden, zou de teller en de noemer met dezelfde hoeveelheid verdelen, op voorwaarde dat de teller en de noemer exact deelbaar zijn door hetzelfde aantal. Maar het is niet mogelijk om, door verdeling te bereiken door hetzelfde gehele getal, een equivalente fractie op basis van 2/3, omdat nummers 2 en 3 neven met elkaar zijn.

Wanneer de teller en noemer van een breuk priemgetallen met elkaar zijn, wordt gezegd dat de breuk is onherleidbaar. En de 2/3 fractie is een goed voorbeeld van dit soort breuken, in feite vertegenwoordigt 2/3 de set van alle breuken die gelijkwaardig zijn aan 0.666 ..

Aan de andere kant is fractie 4/6 herleidbaar en gelijkwaardig aan fractie ⅔, omdat teller 4 en noemer 6 zelfs getallen zijn, beide deelbaar door 2.

Dus de twee manieren om breuken te verkrijgen die gelijkwaardig zijn aan een gegeven, zijn:

• Versterken tegelijkertijd teller en noemer 
• Verminder de teller en de noemer

Versterking van breuken

Om een ​​fractie te verkrijgen die equivalent is aan een gegeven, worden teller en noemer vermenigvuldigd met dezelfde figuur. Hier zijn enkele voorbeelden:

It is concluded that ⅔ (two thirds), 4/6 (four sixth), 6/9 (six ninth) and 8/12 (eight twelfths) are all equivalent fractions with each other, but of them, only ⅔ is the irreducible fractie.

Samenvattend, als u begint met de onherleidbare fractie ⅔, is de manier om een ​​andere equivalente fractie te verkrijgen deze formule toepassen:

Kan u van dienst zijn: opgeloste factorisatieoefeningen

Met een geheel getal.

Versterkingsmethode om gelijkwaardige breuken te verkrijgen. Bron: f. Zapata

Vermindering van breuken

Het is een methode waarmee een equivalente fractie kan worden verkregen, op voorwaarde dat de startfractie een teller en noemer heeft met een of meer gebruikelijke delers.

Het is niet het geval van 2/3, wat zoals eerder gezegd, onherleidbaar is. Maar bijvoorbeeld fractie 60/90 (zestig jaren negentig) Het kan worden gereduceerd tot:

• 6/9, omdat zowel de teller als de noemer deelbaar zijn tussen tien.
• 30/45, omdat teller en noemer deelbaar zijn tussen twee.
• 20/30, omdat teller en noemer deelbaar zijn tussen drie.
• 12/18, omdat teller en noemer deelbaar zijn tussen vijf.

Als u het onherleidbare fractie wilt verkrijgen dat equivalent is aan het origineel, is het noodzakelijk om zowel de teller als de noemer te verdelen door de maximale gemeenschappelijke deler (MCD).

Ontbinden in factoren die de teller heeft:

60 = 2² ⋅ 3 ⋅ 5

En het uitvoeren van dezelfde procedure in de noemer:

90 = 2 ⋅ 3² ⋅ 5

De MCM zijn de gemeenschappelijke prime -factoren met zijn lagere exponent, dat wil zeggen:

MCM (60; 90) = 2⋅3⋅5 = 30

Vervolgens wordt 60 tussen 30 Da 2, die in de teller wordt geplaatst en bij 90 tussen 30 da 3, 3 in de noemer geplaatst. Daarom kan de 60/90 onherleidbare fractie worden uitgedrukt als:

Manieren om te bepalen of een gegeven fractie gelijk is aan 2/3

De directe manier om te weten of twee of meer fracties equivalent zijn, is door de breuken direct op een decimale manier uit te drukken, en als alle cijfers samenvallen, is het zeker dat de breuken gelijkwaardig zijn. Maar er zijn andere methoden van toepassing op 2/3:

Methode 1

Wees fractie x/y u wilt weten of deze fractie gelijk is aan 2/3:

Een ondervragingsbord wordt geplaatst, omdat het nog niet bekend is of de waarden van "x" en "y" voldoen aan gelijkheid. Om het te weten vermenigvuldigt zich in het kruis:

Kan u van dienst zijn: evenredigheidsrelaties: concept, voorbeelden en oefeningen

3x =? 2 en

Alleen wanneer gelijkheid wordt vervuld, is er zekerheid dat X/Y een breuk is die gelijkwaardig is aan 2/3.

Methode 2

Deze methode vereist het bepalen van de maximale gemeenschappelijke deler (MCD) van de teller en de noemer. Dan worden beide gedeeld door de MCD, en als de verkregen fractie na het uitvoeren van de beschreven bewerking 2/3 is, kan worden gezegd dat het een fractie -equivalent is.

Voorbeelden

voorbeeld 1

Bepaal of fractie 40/60 gelijk is aan ⅔.

Oplossing

Door methode 1:

De methode geeft aan dat deze in het kruis moet worden vermenigvuldigd:

40 x 3 =? 60 x 2

120 =? 120

Aangezien gelijkheid wordt vervuld, wordt geconcludeerd dat 40/60 gelijkwaardig is aan 2/3.

Voorbeeld 2

Bepaal of fractie 120/180 gelijk is aan ⅔.

Oplossing

In dit voorbeeld is methode 2 van toepassing. Het eerste is om de ontleding te bepalen in topfactoren van 120:

120 = 2³ ⋅ 3 ⋅ 5

En de ontleding in de noemerfactoren is:

180 = 2² ⋅ 3² ⋅ 5

Om de MCD te bepalen, worden de gemeenschappelijke factoren vermenigvuldigd met zijn lagere exponent:

MCD (120; 180) = 2² ⋅ 3 ⋅ 5 = 60

Dus:

120 ÷ 60 = 2

180 ÷ 60 = 3

Dus wordt geconcludeerd dat 120/180 gelijkwaardig is aan 2/3, dat wil zeggen:

Opgeloste oefeningen

Oefening 1

Zijn breuken 10/15 en 12/18 equivalent?

Oplossing

De snelste manier om het te verifiëren is om zich te vermenigvuldigen tot een kruis, omdat het niet erg grote waarden zijn:

10 x 18 =? 15 x 12

180 =? 180

Er werd een gelijkheid verkregen, dan kan worden gezegd dat 10/15 = 12/18.

Oefening 2

Zijn breuken 8/12 en 12/20 equivalent aan ⅔?

Oplossing

De vereenvoudigingsmethode zal worden toegepast, die bestaat uit het gelijktijdig verdelen van teller en noemer door gemeenschappelijke prime -factoren tot het bereiken van een onherleidbare uitdrukking:

12/12 = 4/6 = ⅔, dat wil zeggen, de eerste fractie is gelijk aan ⅔.

Voor de tweede fractie heb je:

12/20 = 6/10 = ⅗, maar ⅗ is onherleidbaar en verschilt van ⅔, daarom is de tweede fractie niet gelijk aan ⅔.