Fysiek

Elektrische veldstroom

Elektrische veldstroom

Wat is elektrische veldstroom?

Hij elektrische veldstroom of gewoon elektrische stroom is een scalaire hoeveelheid die evenredig is met het aantal elektrische veldlijnen die een oppervlak kruisen. Het wordt aangegeven door de kapitaalbrief Capital φ (phi).

Het elektrische veld "stroomt" niet echt zoals een stroom water, hoewel de stroomleidingen van de vloeistof lijken op die van het elektrische veld.

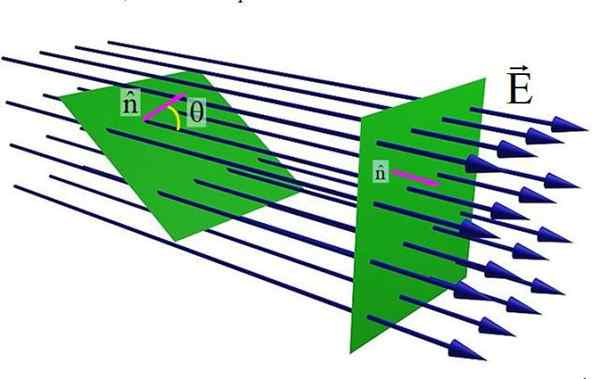
Figuur 1. Elektrisch veld stroming door een plat oppervlak. Bron: Wikimedia Commons.

De bovenste figuur toont een plat oppervlak dat is gekruist door een elektrisch veld EN. Wanneer de normale eenheidsvector naar het oppervlak N en het veld EN Ze zijn parallel, de hoeveelheid veldlijnen die het oppervlak kruist is maximaal. Maar naarmate de hoek θ toeneemt tussen N En EN, Het aantal lijnen dat door het groene oppervlak is gepasseerd, is lager.

Aan de andere kant hangt de elektrische veldstroom ook af van de grootte van EN, Omdat hoe hoger dit, hoe meer veldlijnen ze het oppervlak oversteken. En natuurlijk, hoe groter het S -gebied van het genoemde oppervlak, ook de stroom, dus de volgende vergelijking is vastgesteld:

Φ = E ∙ SOSθ

Deze uitdrukking is consistent met het scalaire product bij de vectoren EN En N:

Φ = (EN • N) S

De eenheid voor elektrische veldstroom in het internationale systeem van eenheden als n is.M2/C (Newton X Square Metro/Coulomb). Als alternatief, aangezien het veld ook wordt gemeten in v/m (volt op metro), bevindt de elektrische stroom zich in (v ∙ m) m).

Voorbeelden

Volgens de definitie kan de elektrische stroom positief, negatief of gelijk zijn aan 0. De elektrische veldstroom is:

Het kan u van dienst zijn: magnetisatie: orbitaal en spin magnetisch moment, voorbeelden

-Positief wanneer de hoek θ tussen EN En N Het is minder dan 90º, omdat de cos θ groter is dan nul.

-Negatief als deze hoek groter is dan 90º, omdat dan cos θ minder is dan nul.

-Nietig wanneer θ precies 90º waard is, omdat cos 90º = 0 en de veldlijnen in dit geval tangentieel zijn naar het oppervlak.

-Aan de andere kant, als de hoek tussen EN En N Het is gelijk aan 0, de stroom verwerft zijn maximale waarde.

Deze mogelijkheden worden weergegeven in de volgende afbeelding:

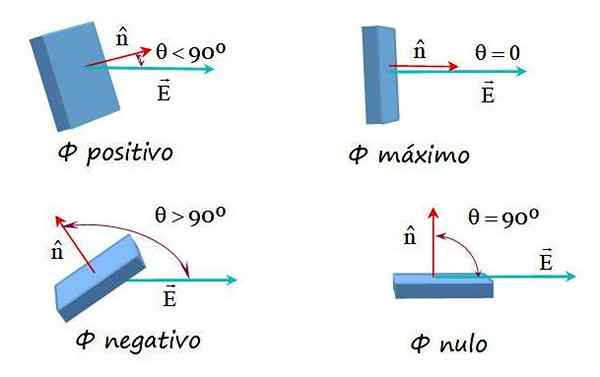Figuur 2. Voorbeelden van elektrische veldstroom met verschillende oriëntaties tussen het veld en de normale oppervlaktevector. Bron: f. Zapata.

Elektrische veldstroom op een willekeurig oppervlak

Eerder werd de elektrische veldstroom bepaald in het specifieke geval van een uniform veld dat een vlak oppervlak beïnvloedde. Voor een willekeurig oppervlak en/of een niet -uniform elektrisch veld, de hoek tussen EN En N kan variëren van punt tot punt.

In de volgende figuur zijn er twee voorbeelden, links een gebogen oppervlak en rechts een gesloten oppervlak.

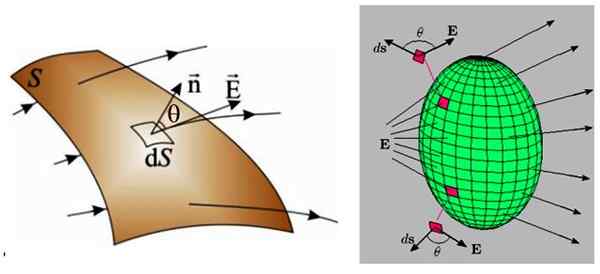figuur 3. Links een willekeurig oppervlak waardoor een niet -uniform elektrisch veld kruist. Rechts rechts kruist een niet -uniform elektrisch veld een gesloten oppervlak, daarom is de netto stroom in dat geval nietig. Bron: f. Zapata.

In beide gevallen is het oppervlak verdeeld in veel kleinere gebieden, van oneindige grootte, ds genoemd, waarvoor het ook een oneindigse stroming kruipt Dφ:

dφ = (EN•N) Ds = (ecosθ) ds

Het totale veld wordt verkregen door al deze infinitesimale bijdragen toe te voegen:

Het symbool van S als een subscript in de integraal geeft aan dat het op het gehele oppervlak moet worden berekend. Als dit wordt gesloten, wordt het aangegeven met een kleine cirkel op de integraal:

Kan u van dienst zijn: Antoine -constanten: formules, vergelijkingen, voorbeelden

In het geval van gesloten oppervlakken, N Wijs er altijd op, dus de stroom heeft een teken + wanneer deze extravert is, omdat de hoek tussen EN En N is minder dan 90º, en teken - wanneer het veld binnenkomt, omdat de hoek tussen EN En N is groter dan 90º (zie figuur 2).

Merk op dat op het gesloten oppervlak aan de rechterkant het aantal veldlijnen dat het oppervlak binnenkomt gelijk is aan het aantal lijnen dat uitkomt. Daarom is de netto stroom, gedefinieerd als de algebraïsche som van de inkomende stroom en de uitgaande stroom, nietig.

De elektrische veldbron bevindt zich in dit geval buiten het oppervlak, maar de netstroom zou verschillen van 0 als de elektrische veldbron (de verdeling van belastingen) in het oppervlak was.

Opdrachten

Oefening 1

Je hebt een elektrisch veld EN = 3.5 kN/c X en een plat rechthoekig oppervlak van 0.35 m breed bij 0.7 m lang. Zoek de elektrische veldstroom die de rechthoek in de volgende gevallen kruist:

a) Het oppervlak is parallel aan het vlak yz.

b) De rechthoek is parallel aan het XY -vlak.

c) Het normale vlak vormt een hoek van 40º met de x -as en bevat de as en.

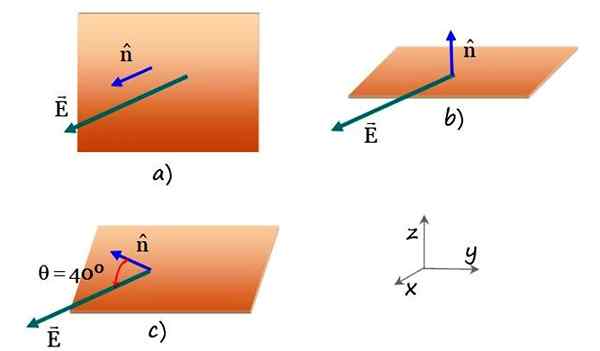Figuur 4. Een rechthoekig vlak gekruist door een uniform elektrisch veld in verschillende vlakke oriëntaties. Bron: f. Zapata.

Oplossing voor

De normale vector en de elektrische veldvector zijn parallel, daarom is de hoek θ tussen de twee 0º en de elektrische stroom is:

Φ = (e ∙ s) cos 0 = e ∙ s

Het S -gebied van de rechthoek is:

Kan u van dienst zijn: Parallellogram -methode: voorbeelden, opgeloste oefeningen

S = 0.35 m x 0.7 m = 0.245 m2

Vervangen in φ:

Φ = e ∙ s = 3.5 x 103 N/C × 0.245 m2 = 857.5 n ∙ m2 /C.

Oplossing B

De elektrische veldstroom is 0, omdat de vectoren EN En N Ze staan ​​loodrecht op elkaar.

Oplossing C

De hoek θ tussen het veld EN en de normale vector N is dus 40º (zie figuur), dus:

Φ = e ∙ s ∙ cos θ = 3.5 x 103 N/C × 0.245 m2 × cos 40º = 656.9 n ∙ m2 /C.

Oefening 2

Bereken de elektrische veldstroom die een positieve punctuele belasting produceertof = 2μC in het midden van een straal bol r = 5 cm.

Oplossing

Het veld geproduceerd door de belasting Qof Het is niet uniform, maar uit de Coulomb -wet is bekend dat het op het oppervlak van de bol een omvang heeft van:

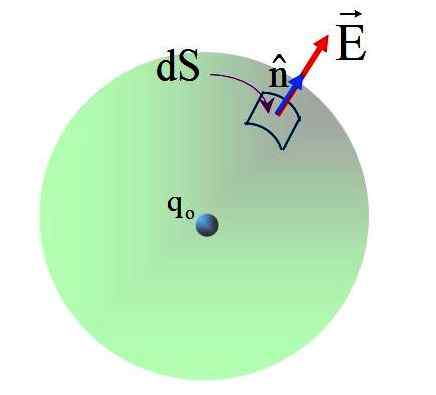Figuur 5. Vliegen van het veld geproduceerd op het oppervlak van de bol door een punctuele belasting in het midden. Bron: f. Zapata.

Het veld heeft radiale richting en de normale vector N, Daarom is de hoek tussen de twee vectoren 0 op elk punt van het sferische oppervlak. Vervangen:

Je moet:

DS's integrale op het hele sferische oppervlak is het gebied ervan, dat is 4πr2, daarom:

Die concludeert dat de elektrische veldstroom niet afhankelijk is van de oppervlakte, maar van de belasting erin vergrendeld.

De waarde ervan is:

Φ = 4π × 9 × 109 x 2 × 10-6 N⋅m2/C = 2.3 x 105 N⋅m2/C

Referenties

  1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
  2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 5. Elektrostatica. Uitgegeven door Douglas Figueroa (USB).
  3. Giambattista, een. 2010. Natuurkunde. 2e. ED. McGraw Hill.
  4. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
  5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.