Gemeenschappelijke factor voor het groeperen van termen voorbeelden, oefeningen

Hij Gemeenschappelijke factor voor het groeperen van termen Het is een algebraïsche procedure die het schrijven van enkele algebraïsche uitdrukkingen mogelijk maakt in de vorm van factoren. Om dit doel te bereiken, moet de uitdrukking eerst gemakkelijk groeperen en waarnemen dat elke aldus gevormde groep in feite een gemeenschappelijke factor heeft.

Het correct toepassen van de techniek vereist enige oefening, maar in korte tijd is het mogelijk om te domineren. Laten we eerst een illustratief voorbeeld bekijken, stap voor stap beschreven. Dan kan de lezer toepassen wat ze hebben geleerd in elk van de oefeningen die erna zullen verschijnen.

Figuur 1. Verwijder de gemeenschappelijke factor voor het groeperen van termen om het werk met algebraïsche uitdrukkingen te vergemakkelijken. Bron: Pixabay.

Stel bijvoorbeeld dat u rekening moet houden met de volgende uitdrukking:

2x² + 2xy - 3zx - 3zy

Deze algebraïsche expressie bestaat uit 4 monomials of termen, gescheiden door tekens + en -, namelijk:

2x², 2xy, -3zx, -3zy

Zorgvuldig observeren, is de X gemeenschappelijk voor de eerste drie, maar niet voor de laatste, terwijl de en is gemeenschappelijk voor de tweede en de vierde, en de z is gemeenschappelijk voor de derde en de vierde.

Dus in principe is er geen gemeenschappelijke factor aan de vier termen tegelijkertijd, maar als ze worden gegroepeerd zoals deze in de volgende sectie wordt weergegeven, kan men de uitdrukking helpen schrijven als het product van twee of meer factoren.

[TOC]

Voorbeelden

Factor de uitdrukking: 2x² + 2xy - 3zx - 3zy

Stap 1: Groep

2x² + 2xy - 3zx - 3zy = (2x² + 2xy) + (-3zx - 3zy)

Stap 2: Verwijder de gemeenschappelijke factor uit elke groep

2x² + 2xy - 3zx - 3zy =

= (2x² + 2xy) - (3zx + 3zy) =

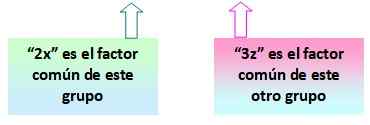
= 2x (x+y) - 3z (x+y)

JeMportante: Het negatieve teken is ook een gemeenschappelijke factor waarmee rekening moet worden gehouden.

Kan u van dienst zijn: Vector Space: Base en Dimension, Axioms, Properties

Merk nu op dat de haakjes (x+y) wordt herhaald in de twee verkregen termen bij de groepering. Dat is de gemeenschappelijke factor die zocht.

Stap 3: Factoriseer alle expressie

2x² + 2xy - 3zx - 3zy = (x+y) (2x - 3z)

Met het vorige resultaat is het doel van de factorisatie bereikt, wat niemand minder is dan het transformeren van een algebraïsche expressie op basis van bedragen en aftrekking van termen, in het product van twee of meer factoren, in ons voorbeeld, van: (x+ y) en (2x - 3z).

Belangrijke kwesties over de gemeenschappelijke groepsfactor

Vraag 1: Hoe te weten dat het resultaat correct is?

Antwoord: Distributieve eigenschap wordt toegepast op het verkregen resultaat en na het verminderen en vereenvoudigen, de aldus bereikt uitdrukking moet samenvallen met het oorspronkelijke, zo niet, er is een fout.

In het vorige voorbeeld werkt het omgekeerd met het resultaat om te controleren of het prima is:

(x+y) (2x - 3z) = 2x² -3zx +2xy - 3zy

Aangezien de volgorde van de addends de som niet wijzigt, zijn er na het toepassen van de distributieve eigenschap alle oorspronkelijke termen tekens. Daarom is de factorisatie correct.

Vraag 2: Had je op een andere manier gegroepeerd?

Antwoord: Er zijn algebraïsche uitdrukkingen die meer dan één vorm van groepering toelaten en anderen die dat niet doen. In het geselecteerde voorbeeld kan de lezer andere mogelijkheden proberen, bijvoorbeeld groepering:

2x² + 2xy - 3zx - 3zy = (2x²- 3zx) + (2xy - 3zy)

En u kunt zien dat het resultaat hetzelfde is als hier verkregen. Het vinden van de optimale groep is een kwestie van praktijk.

Kan u van dienst zijn: Cotangent afgeleid: berekening, demonstratie, oefeningen

Vraag 3: Waarom is het nodig om een ​​gemeenschappelijke factor te krijgen uit een algebraïsche uitdrukking?

Antwoord: Omdat er toepassingen zijn waarin de gefactoriseerde uitdrukking berekeningen vergemakkelijkt. Stel bijvoorbeeld dat u 2x wilt doen² + 2xy - 3zx - 3zy gelijk aan 0. Wat zouden de mogelijkheden zijn?

Om deze zorg te reageren, is de gefactoriseerde versie veel nuttiger dan de oorspronkelijke ontwikkeling in termen. Het ontstaat als deze:

(x+y) (2x - 3z) = 0

Een mogelijkheid dat de uitdrukking 0 waard is, is dat x = -y, ongeacht de waarde van z. En de andere is dat x = (3/2) z, zonder de waarde van y te doen aan.

Opdrachten

- Oefening 1

Krijg de gemeenschappelijke factor van de volgende expressie door het groeperen van termen:

AX+AY+BX+door

Oplossing

De eerste twee zijn gegroepeerd, met de gemeenschappelijke factor "A" en de laatste twee met de gemeenschappelijke factor "B":

Ax+Ay+Bx+door = a (x+y)+b (x+y)

Zodra dit is gedaan, wordt een nieuwe gemeenschappelijke factor onthuld, die (x+y) is, zodat:

Ax+Ay+Bx+door = a (x+y)+b (x+y) = (x+y) (a+b)

Een andere manier om te groeperen

Deze uitdrukking geeft een andere manier van groepering toe. Laten we eens kijken wat er gebeurt als de termen worden herschikt en er een groep wordt gemaakt waarmee ze X en een andere bevatten met die die bevatten en:

Ax +Ay +Bx +door = Ax +Bx +Ay +By = X (A +B) +Y (A +B)

Op deze manier is de nieuwe gemeenschappelijke factor (A+B):

Ax+Ay+Bx+door = Ax+Bx+Ay+door = X (A+B)+Y (A+B) = (X+Y) (A+B)

Dat leidt tot hetzelfde resultaat van de eerste manier van groeperen dat het werd getest.

- Oefening 2

Het is vereist om de volgende algebraïsche expressie te schrijven als het product van twee factoren:

3e³ - 3e²B+9AB²-naar²+AB-3B²

Kan u van dienst zijn: Coplanares -punten: vergelijking, voorbeeld en opgeloste oefeningen

Oplossing

Deze uitdrukking bevat 6 termen. Laten we proberen te groeperen als eerste en vierde, tweede en derde en uiteindelijk vijfde en zesde:

3e³ - 3e²B+9AB²-naar²+AB-3B² = (3e³ -naar²) + (- 3e²B+9AB²) + (AB-3B²))

Nu is elke haakjes factor:

= (3e³ -naar²) + (- 3e²B+9AB²) + (AB -3B²) = a² (3a -1) + 3ab (3b -a) + b (a -3b)

Op het eerste gezicht lijkt het erop dat de situatie ingewikkeld is, maar de lezer moet niet worden ontmoedigd, omdat we de laatste termijn gaan herschrijven:

naar² (3a -1) + 3ab (3b -a) + b (a -3b) = a² (3a - 1) + 3ab (3b -a) - b (3b -a)

De laatste twee termen hebben nu een gemeenschappelijke factor, die (3b-a) is, zodat ze kunnen worden gefactoriseerd. Het is heel belangrijk om de eerste termijn niet uit het oog te verliezen² (3a - 1), die alles moet blijven begeleiden als toevoegen, zodat u niet met hem werkt:

naar² (3a - 1) + 3ab (3b -a) - b (3b -a) = a² (3A-1) + (3B-A) (3AB-B)

De uitdrukking is teruggebracht tot twee termen en een nieuwe gemeenschappelijke factor wordt ontdekt in de laatste, die "B" is. Nu blijft het:

naar² (3a-1) + (3b-a) (3ab-b) = a² (3A-1) +B (3B-A) (3A-1)

De volgende gemeenschappelijke factor bij het verschijnen is 3e - 1:

naar² (3a - 1) +b (3b -a) (3a -1) = (3a - 1) [a² + B (3B-A)]

Of als u de voorkeur geeft aan zonder vierkante haakjes:

(3e - 1) [A² + B (3b -a)] = (3a - 1) (a² -AB + 3B²))

Kan de lezer een andere manier van groeperen vinden die tot hetzelfde resultaat leidt?

Figuur 2. Voorgestelde factorisatie -oefeningen. Bron: f. Zapata.

Referenties

1. Baldor, een. 1974. Elementaire algebra. Venezolaanse culturele S.NAAR.
2. Jiménez, r. 2008. Algebra. Prentice Hall.
3. Belangrijkste gevallen van factorisatie. Hersteld van: Julioprofe.netto.
4. UNAM. Basic Mathematics: factorisatie door termen te groeperen. Faculteit van boekhouding en administratie.
5. Zill, D. 1984. Algebra en trigonometrie. MacGraw Hill.