Evaluatie van functies

Om een ​​functie te evalueren waarvan het diagram bekend is, is het voldoende om het overeenkomstige element in de aankomstset te observeren voor een bepaalde waarde of element van de startset. Bron: f. Zapata.

Wat is de evaluatie van functies?

De Evaluatie van functies Het bestaat uit het bepalen van het beeld van een bepaalde domeinwaarde. Met andere woorden, voor een bepaalde waarde van de startset moet u de overeenkomst vinden in de aankomstset.

Een functie kan op verschillende manieren worden weergegeven. Als bijvoorbeeld het Venn -diagram beschikbaar is, is de evaluatie zeer eenvoudig, is het voldoende om het element van de start- of domeinset te selecteren en het element te bekijken dat overeenkomt met de aankomstset.

In het "…… is kapitaaldiagram ...", hierboven weergegeven, bij het evalueren van deze functie in het "Canada" -element, is het het "Ottawa" -element, in geval van "Mexico", het is "Mexico City" en spoedig.

Als de functie wordt gegeven in de vorm van nette paren, is de evaluatie ook eenvoudig: het tweede lid van het ordelijke koppel is het beeld van het eerste lid. Bijvoorbeeld, met de functie f (x) beschreven door:

f (x) = (0.0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Bij het evalueren van de functie voor waarde 3 is het resultaat 6; Bij het evalueren van 5 is het 10 enzovoort.

Evenzo kan een functie worden geëvalueerd wanneer de grafiek beschikbaar is, op voorwaarde dat de waarde die u wilt evalueren, erin verschijnt.

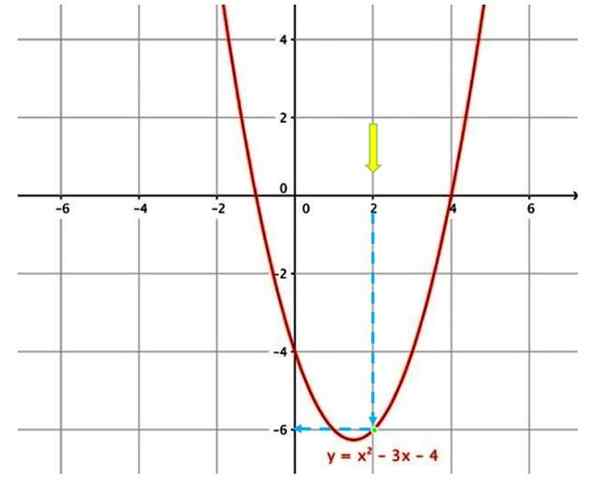Grafiek om een ​​functie te evalueren

Om bijvoorbeeld de hierboven getoonde functie te evalueren, bij x = 2, is het eerste om te vinden in grafiek A x = 2 (gele pijl).

Vervolgens moet je de blauwe verticale pijl verplaatsen, totdat je de curve aanraakt (groen punt). Volg de blauwe pijl opnieuw, die de overeenkomstige waarde op de verticale as aangeeft, daarom wordt bij het evalueren van de functie bij x = 2, y = −6 verkregen.

Het kan u van dienst zijn: Trigonometrische functies: Basic, in het Cartesiaanse vlak, voorbeelden, oefening

Evalueer een bepaalde functie in de wiskundige notatie

In het onderste deel van de bovenstaande grafiek verschijnt de grafische functie, maar gegeven in de wiskundige notatie, dat wil zeggen via een formule:

f (x) = x² - 3x - 4

Wanneer u de functie in elke waarde x = a wilt evalueren, moet u f (a) vinden, die eenvoudig wordt gelezen "f van een".

Om het resultaat te vinden, wordt x = a vervangen in de functieformule en worden de gevraagde bewerkingen en berekeningen daar uitgevoerd.

Stel dat u de functie van het voorbeeld wilt evalueren op x = −1. Dit betekent dat F (−1) moet worden gevonden.

De eerste stap is om x = -1 in de functie te vervangen:

f (−1) = (−1)² - 3 ∙ (−1) - 4

En voer vervolgens de aangegeven bewerkingen uit, die in dit voorbeeld zijn:

• Zoek het vierkant van −1: (−1)² = 1
• Trek de vorige waarde van product 3 ∙ (−1) af: 3 ∙ (−1) = −3
• Vanuit het vorige resultaat, trek 4 af 4

f (−1) = (−1)² - 3 ∙ (−1) - 4 = 1 + 3 - 4 = 0

De lezer kan dit resultaat bevestigen, uit de grafiek van de functie.

De beschreven procedure kan worden gebruikt om de functie bij elke andere domeinwaarde te evalueren. U kunt bijvoorbeeld F (-2), F (100) of zelfs F (H) vinden, waarbij H een willekeurige variabele waarde is, die tot het domein van de functie behoort.

Evalueer een functie op een waarde x = h 

Stel dat u de functie op een willekeurige waarde wilt evalueren, een frequente werking in wiskundige berekening.

In dit geval wordt X vervangen door H, op dezelfde manier die wordt gedaan wanneer X elke numerieke waarde neemt, en het resultaat is zoveel mogelijk vereenvoudigd.

Wanneer de resulterende bewerking niet langer kan worden vereenvoudigd, blijft de resulterende bewerking over.

Het kan u van dienst zijn: Enegon: Eigenschappen, hoe u een enegon kunt maken, voorbeelden

Voorbeeld

U wilt de functie f (x) = x evalueren² - 3x - 4 bij x = h+1. De noodzakelijke aanpak is als volgt:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4

Rechts van gelijkheid is de eerste term een ​​opmerkelijk product:

(H+1)² = h² +2H + 1

De volgende term wordt opgelost via distributieve eigenschap:

3 ∙ (H + 1) = 3H + 3

Wanneer u al het bovenstaande vervangt, hebt u:

f (h+1) = (h+1)² - 3 ∙ (H+1) - 4 = H² +2H + 1 - (3H + 3) - 4

De vergelijkbare termen worden verminderd, door algebraïsche som:

f (h+1) = h² + 2H + 1 - 3H - 3 - 4 = H² - H - 6

Het differentiaalquotiënt

Het differentiële quotiënt of de verhouding tussen verschillen D van een functie f (x) wordt gedefinieerd als:

Met voorwaarde h ≠ 0, wat nodig is, omdat de verdeling door 0 niet is gedefinieerd.

Dit quotiënt wordt geometrisch geïnterpreteerd als de helling van een Secant -lijn ten opzichte van de curve, dat wil zeggen een lijn die twee punten ervan doorloopt. De coördinaten van deze punten zijn: [x, f (x)] en [x+h; f (x+h)], zoals te zien in de volgende figuur:

Het differentiële quotiënt is gelijk aan het berekenen van de helling van de Secant -lijn naar de curve, die door de aangegeven punten doorgaat. Bron: Wikimedia Commons.

Dat is de reden waarom dit quotiënt verschijnt in de berekening van de afgeleide van een functie, omdat het maken van de "H" -benadering de waarde 0, de Secant -lijn heeft de neiging een raaklijn te worden op het punt (x, y), omdat de punten in het kruispunt van De figuur is zo dichtbij dat ze naar hetzelfde punt neigen.

Aldus wordt de lijn raaklijn (onderschept de curve in een enkel punt).

Dit is precies de definitie van afgeleid van een functie: de helling van de lijn raakt naar de curve in coördinaatpunt (x, f (x))).

Het kan u van dienst zijn: gewogen media: hoe het wordt berekend, voorbeelden en oefeningen

Zoals te zien is, vereist het differentiaalquotiënt de functie evalueren in (x + h) en in x. De volgende voorbeelden illustreren hoe het te doen.

voorbeeld 1

U wilt het differentiaalquotiënt van de functie f (x) = 2x - 3 vinden. De eerste stap is om de evaluatie van de functie voor x = x + h te verhogen, zoals deze:

f (x+h) = 2 ∙ (x+h) - 3 = 2x+2h - 3

Vervolgens wordt het resultaat vervangen in de definitie van D, eerder gegeven:

Met H ≠ 0.

De teller is zo ver mogelijk vereenvoudigd, waardoor vergelijkbare termen worden verminderd:

Ten slotte zijn de gemeenschappelijke factoren in teller en noemer vereenvoudigd:

D = 2

Voorbeeld 2

Zoek het differentiaalquotiënt van de functie f (x) = x² - 3x - 4.

We gaan verder zoals in het vorige voorbeeld, het vinden van eerste F (x+H), het resultaat vervangen in D en vereenvoudigt tot het maximum:

f (x+h) = (x+h)² - 3 (x+h) - 4 = x² + 2HX + H² - 3x - 3H - 4

= 2x+H-3

Daarom:

D = 2x+H-3

Waar h ≠ 0.

Opgeloste oefeningen

Oefening 1

Evalueer de functie f (x) = 2x² - 4x + 1 wanneer:

a) x = -1
b) x = 0
c) x = 2

Oplossing voor

F (-1) = 2 (-1)² - 4 (-1) + 1 = 2 + 4 + 1 = 7

Oplossing B

f (0) = 2 (0)² - 4 (0) + 1 = 0 - 0 + 1 = 1

Oplossing C

F (2) = 2 ∙ 2² - 4 ∙ 2 + 1 = 8 - 8 + 1 = 1

Oefening 2

Een natuurbeschermend team bepaalde dat de functie w (t) = 0.Lt² + 1.8t dient om de hoeveelheid afval "W" te modelleren, in kilogram, die in een bepaalde rivier worden gegooid, in een tijd "T", gegeven in dagen.

Bereken de hoeveelheid afval die in de rivier wordt gegooid aan het einde van:

a) 3 dagen
b) 1 week
c) 1 maand

Oplossing voor

W (t) functie wordt geëvalueerd op t = 3 dagen:

W (3) = 0.1 × 3² +1.8 × 3 = 0.9 + 5.4 = 6.3 kilogram

Oplossing B

Voordat u evalueert, moet u 1 week tot dagen doorbrengen:

1 week = 7 dagen

W (7) = 0.1 × 7² +1.8 × 7 = 4.9 + 12.6 = 17.5 kilogram

Oplossing C

Nogmaals, het is noodzakelijk om de maanden tot dagen te transformeren:

1 maand = 30 dagen

W (30) = 0.1 × 30² +1.8 × 30 = 90 + 54 = 144 kilogram

Referenties

1. Larson, r. 2012. Voorzetting. 8e. Editie. Cengage leren.
2. Monterey Institute. Functies evalueren. Hersteld van: Montereyinstitute.borg.
3. Stewart, J. 2007. Precculment: wiskunde voor berekening. 5e. Editie. Cengage leren.
4. Sullivan, m. 1997. Voorzetting. 4e. Editie. Pearson Education.
5. Zill, D. 2008. Voorrang op berekening vooruitgang. 4e. Editie. McGraw Hill.