Standaard schatting Fout hoe berekend, voorbeelden, oefeningen

Hij Standaardschattingfout Meet de afwijking in een steekproefpopulatiewaarde. Dat wil zeggen, de standaard schattingfout meet de mogelijke variaties van het steekproefgemiddelde ten opzichte van de werkelijke waarde van het bevolkingsgemiddelde.

Als u bijvoorbeeld de gemiddelde leeftijd van de bevolking van een land (bevolkingsgemiddelde) wilt weten, wordt een kleine groep inwoners genomen, die we zullen noemen "shows". Daaruit wordt de gemiddelde leeftijd (steekproefgemiddelde) geëxtraheerd en wordt aangenomen dat de populatie die gemiddelde leeftijd heeft met een standaardramingsfout die min of meer varieert.

M. W. Toews [CC door 2.5 (https: // creativeCommons.Org/licenties/door/2.5)]

Opgemerkt moet worden dat het belangrijk is om de standaardafwijking niet te verwarren met de standaardfout en de standaardramingsfout:

1- De standaardafwijking is een maat voor gegevensverspreiding; dat wil zeggen, het is een maat voor populatievariabiliteit.

2- De standaardfout is een maat voor de variabiliteit van het monster, berekend op basis van de standaardafwijking van de populatie.

3- De standaardschattingsfout is een maat voor de fout die wordt gemaakt bij het nemen van het steekproefgemiddelde als een schatting van het populatiegemiddelde.

[TOC]

Hoe wordt het berekend?

De standaardramingfout kan worden berekend voor alle in de monsters verkregen maatregelen (bijvoorbeeld standaard gemiddelde schattingsfout of standaardfout van standaardafwijkingsschatting) en meet de fout die wordt gemaakt bij het schatten van de werkelijke populatiemaat

Uit de standaard schattingsfout is het betrouwbaarheidsinterval van de overeenkomstige maatregel gebouwd.

Kan u van dienst zijn: omgekeerde matrix: berekening en oefening opgelost

De algemene structuur van een formule voor de standaardramingsfout is als volgt:

Standaardschatting Fout = ± Trustcoëfficiënt * Standaardfout

Vertrouwencoëfficiënt = limietwaarde van een steekproefstatistiek of bemonsteringsverdeling (normaal of Gauss Bell, Student T, onder andere) voor een bepaald interval van waarschijnlijkheden.

Standaardfout = standaardafwijking van de populatie gedeeld door de vierkante wortel van de steekproefgrootte.

De betrouwbaarheidscoëfficiënt geeft de hoeveelheid standaardfouten aan die bereid zijn om op maat gemaakt toe te voegen en af ​​te trekken om een ​​bepaald niveau van vertrouwen in de resultaten te hebben.

Voorbeelden van berekening

Neem aan dat u probeert het aandeel mensen in de bevolking te schatten die een gedrag A heeft, en u wilt 95% vertrouwen in hun resultaten hebben.

Een steekproef van N -mensen wordt genomen en de steekproefverhouding P en de complement q wordt bepaald.

Standaardramingsfout (EEE) = ± Trustcoëfficiënt * Standaardfout

Vertrouwencoëfficiënt = z = 1.96.

Standaardfout = de vierkantswortel van de reden tussen het product van de steekproefverhouding voor zijn complement en de grootte van het monster N.

Uit de standaardramingsfout wordt het interval waarin de populatieverhouding of het monster van andere monsters die uit die populatie kunnen worden gevormd, wordt vastgesteld, met 95% betrouwbaarheidsniveau:

P -eee ≤ populatie aandeel ≤ p + eee

Opgeloste oefeningen

Oefening 1

1- Stel dat u probeert het aandeel mensen in de bevolking te schatten die de voorkeur hebben voor een verrijkte zuivelformule, en u wilt 95% vertrouwen in hun resultaten hebben.

Kan u van dienst zijn: synthetische verdeling

Een steekproef van 800 mensen wordt genomen en er wordt vastgesteld dat 560 mensen in de steekproef de voorkeur hebben voor de verrijkte zuivelformule. Bepaal een interval waarin het bevolkingsaandeel kan worden verwacht en het aandeel van andere monsters die uit de bevolking kunnen worden genomen, met 95% vertrouwen

a) Laten we de steekproefverhouding P en het aanvullen ervan berekenen:

P = 560/800 = 0.70

Q = 1 -P = 1 -0.70 = 0.30

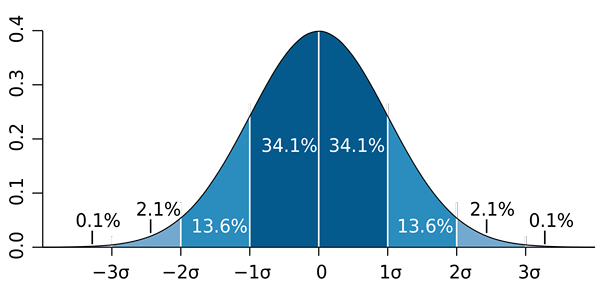
b) Het is bekend dat het aandeel een normale verdeling nadert naar grote monsters (groter dan 30). Vervolgens wordt de SO -aangeduurde regel 68 - 95 - 99 toegepast.7 en je moet:

Vertrouwencoëfficiënt = z = 1.96

Standaardfout = √ (p*q/n)

Standaardschattingsfout (EEE) = ± (1.96)*√ (0.70)*(0.30)/800) = ± 0.0318

c) Uit de standaardschattingsfout wordt het interval waarin het bevolkingsverhoudingsverhoudingsverhouding wordt verwacht met 95% betrouwbaarheidsniveau vastgesteld:

0.70 -0.0318 ≤ populatie aandeel ≤ 0.70 + 0.0318

0.6682 ≤ populatie aandeel ≤ 0.7318

U kunt verwachten dat de steekproef van 70% tot 3 zal veranderen.18 procentpunten als er een andere steekproef van 800 individuen nodig is of dat het reële deel van de bevolking tussen 70 - 3 ligt.18 = 66.82% en 70 + 3.18 = 73.18%.

Oefening 2

2- We zullen van Spiegel en Stephens, 2008 nemen, de volgende case study:

Van de totale wiskundecijfers van de eerste studenten van een universiteit, werd een willekeurige steekproef van 50 kwalificaties genomen waarin het gemiddelde gevonden 75 punten was en de standaardafwijking, 10 punten. Wat zijn de betrouwbaarheidslimieten van 95% voor de schatting van het gemiddelde van de wiskundekwalificaties van de universiteit?

Het kan u van dienst zijn: wat is de relatie tussen het rhombusgebied en de rechthoek?

a) Laten we de standaardramingsfout berekenen:

95%betrouwbaarheidscoëfficiënt = z = 1.96

Standaardfout = S/√n

Standaardschattingsfout (EEE) = ± (1.96)*(10√50) = ± 2.7718

b) Uit de standaardramingsfout is het interval waarin het populatiegemiddelde of het gemiddelde van een andere steekproef 50 wordt vastgesteld, met 95% betrouwbaarheidsniveau:

50 -2.7718 ≤ bevolkingsgemiddelde ≤ 50 + 2.7718

47.2282 ≤ bevolkingsgemiddelde ≤ 52.7718

c) U kunt verwachten dat het gemiddelde van de steekproef maximaal 2 zal veranderen.7718 punten Als een andere steekproef van 50 graden wordt gehaald of dat het reële gemiddelde van de wiskundecijfers van de bevolking van de universiteit tussen 47 ligt.2282 punten en 52.7718 punten.

Referenties

1. ABRAIRA, V. (2002). Standaardafwijking en standaardfout. Semergen magazine. Web hersteld.Archief.borg.
2. Rumsey, D. (2007). Tussenliggende statistieken voor dummies. Wiley Publishing, Inc.
3. Salinas, h. (2010). Statistieken en waarschijnlijkheden. Hersteld van mat.Uda.Klet.
4. Sokal, r.; Rohlf, f. (2000). Biometrie. De principes en praktijk van statistieken in biologisch onderzoek. Derde Ed. Blume -edities.
5. Spiegel, m.; Stephens, L. (2008). Statistieken. Vierde Ed. McGraw-Hill/Inter-American uit Mexico S. NAAR.
6. Wikipedia. (2019). 68-95-99.7 regel. Opgehaald van.Wikipedia.borg.
7. Wikipedia. (2019). Standaardfout. Opgehaald van.Wikipedia.borg.