Willekeurige foutformule en -vergelijkingen, berekening, voorbeelden, oefeningen

Hij willekeurige fout van een fysiek bedrag bestaat uit de niet -voorspelbare variaties van de maat van die hoeveelheid. Deze variaties kunnen worden geproduceerd door het fenomeen dat wordt gemeten, door het meetinstrument of door de waarnemer zelf.

Een dergelijke fout is niet te wijten aan het feit dat er tijdens het experiment iets mis is gedaan, maar dat het een fout is die inherent is aan het meetproces of het bestudeerde fenomeen. Dit veroorzaakt de maatregel die soms een beetje groter en soms een beetje lager is, maar oscilleert meestal rond een centrale waarde.

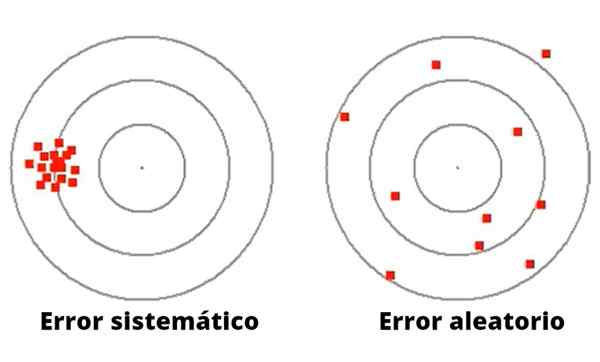
Figuur 1- Willekeurige fouten variëren in grootte en richting. Integendeel, systematische fouten zijn meestal consistent.

In tegenstelling tot willekeurige fout, kan systematische fout worden veroorzaakt door slechte kalibratie of een ongepaste schaalfactor in het meetinstrument, inclusief een storing in de experimentele apparatuur, of een ongepaste observatie, die een afwijking in dezelfde zin veroorzaakt.

Figuur 1 illustreert het verschil tussen systematische en willekeurige fout in het DART -startspel naar een doelwit met cirkels.

In het geval van links zijn de pijlen geconcentreerd rond een zeer ver van het midden. De werper van deze pijltjes, hoewel met een goed doel, heeft een systematisch falen, misschien van visuele oorsprong, of in de weg van gooien.

Aan de andere kant heeft de werper aan de rechterkant (in figuur 1) een grote dispersie rond het centrale doelwit, daarom is het een zeer onnauwkeurige werper, met een slecht doel, die onvrijwillig willekeurige fout maakt.

[TOC]

Formules en vergelijkingen in willekeurige fout

Wanneer het meetproces willekeurige fout vertoont, is dit noodzakelijk.

Natuurlijk is het in elke meting noodzakelijk om ervoor te zorgen dat de omstandigheden waarin ze worden uitgevoerd altijd hetzelfde zijn.

Kan u dienen: Faraday Law: Formule, eenheden, experimenten, oefening,

Stel dat de meting is herhaald N keer. Omdat er een willekeurige fout is in elke meting, is er een iets andere waarde. Stel dat de set van N Metingen zijn:

X₁, X₂, X₃,…, X_N

Dus welk waarderapport voor maatregel? 

Gemiddelde waarde en standaardafwijking

De middelwaarde of gemiddeld van de reeks maatregelen, die we aangeven en wordt als volgt berekend:

= (x₁ + X₂ + X₃ +… +X_N) / N

Standaardafwijking

Dit resultaat heeft echter een foutmarge gegeven door de standaardafwijking. Om het te definiëren, moet u eerst de afwijking en vervolgens de variantie kennen:

-De afwijking D_Je  dat elke gemeten waarde heeft Xi Wat betreft de gemiddelde waarde is:

D_Je = x_Je -

Als het gemiddelde van de afwijkingen zou worden berekend, zou het systematisch worden verkregen = 0, Gezien dat: 

= (D₁ + D₂ + D₃ +… +D_N) /n =

= [x₁ - ) + (x₂ - ) +… +(X_N - )]/N

= (x₁+ X₂ +… + X_N) / n - n / n = - = 0

-Het gemiddelde van afwijkingen is niet nuttig om de dispersie van de maatregelen te kennen. Aan de andere kant, de gemiddelde waarde van het kwadraat van afwijkingen of variantie, aangegeven door σ², Ja dat is zo.

Het wordt berekend volgens de volgende formule:

σ² = (D₁² + D₂² +.. .+ D_N² ) / (N -1)

In statistieken wordt dit bedrag genoemd variantie.  

En bij de vierkantswortel van de variantie staat het bekend als Standaardafwijking σ:

σ = √ [(D₁² + D₂² +.. .+ D_N² ) / (n -1)] 

De standaardafwijking σ geeft aan dat:

1.- 68% van de genomen metingen is opgenomen in de interval [ - σ, + σ]. 

2.- 95% van de metingen is in het interval [ - 2σ, + 2σ].

3.- 99,7% van de genomen maatregelen ligt in het bereik [ - 3σ, + 3σ].

Hoe wil een willekeurige fout berekenen?

Het meetresultaat is het middelwaarde van de N Metingen aangegeven door en berekend volgens de volgende formule:

Kan u van dienst zijn: Areolaire snelheid: hoe het wordt berekend en opgeloste oefeningen

= (∑x_Je) / N

Het is echter niet de "exacte" waarde van de meting, omdat deze wordt beïnvloed door de Willekeurige fout ε, die zo is berekend:

ε = σ / √n

Waar:

σ = √ [(∑ (xi -)² ) / (n -1)]

Het uiteindelijke resultaat van de meting moet op een van de volgende manieren worden gerapporteerd:

1. ± σ / √n = ± ε Met een betrouwbaarheidsniveau van 68%.
2. ± 2σ / √n = ± 2ε Met een betrouwbaarheidsniveau van 95%.
3. ± 3σ / √n = ± 3ε Met een betrouwbaarheidsniveau van 99,7%.

De willekeurige fout beïnvloedt het laatste significante cijfer van de meting, die meestal samenvalt met de waardering van het meetinstrument. Als de willekeurige fout echter erg groot is, kunnen de laatste twee significante cijfers worden beïnvloed door variatie.

Willekeurige foutvoorbeelden

Willekeurige fouten kunnen in verschillende gevallen verschijnen waarin een maat wordt gemaakt:

Het meten van een lengte met een meetlint of regel

Wanneer een lengte wordt gemeten met een regel of een meetlint en de metingen tussen de merken van de schaal vallen, wordt die tussentijdse waarde geschat.

Soms heeft de schatting overtollig en ander defect, dus er wordt een willekeurige fout in het meetproces geïntroduceerd.

Figuur 2. Willekeurige fouten kunnen verschijnen wanneer een lengte wordt gemeten met een tape -tape. Bron: Pikrepo.

De snelheid van de wind

Bij de meting van de snelheid van de wind kunnen er veranderingen zijn in het lezen van het ene moment naar het andere, vanwege de veranderende aard van het fenomeen.

Bij het lezen van het volume in een afgestudeerde cilinder

Wanneer het volume wordt gelezen met een afgestudeerde cilinder, zelfs probeert om de parallage -fout te minimaliseren, elke keer dat deze wordt gemeten, verandert de meniscale observatiehoek een beetje, daarom worden de maatregelen beïnvloed door willekeurige fout.

Het kan u van dienst zijn: Eerste evenwichtstoestand: uitleg, voorbeelden, oefeningen figuur 3.- In het chemielaboratorium is het mogelijk om willekeurige fouten te maken bij het lezen van een afgestudeerde cilinder. Bron: Pexels.

Wanneer de status van een kind wordt gemeten

Door de hoogte van een kind te meten, vooral als het een beetje rusteloos is, maakt het kleine houdingswijzigingen enigszins verandert lezen en.

Bij gebruik van de badkamerschaal

Wanneer we ons gewicht met een badkamer willen meten, een kleine verandering in het ondersteuningspunt, kan zelfs een positieverandering willekeurig de meting beïnvloeden.

Oefening opgelost

Een speelgoedwagen mag langs een rechte en hellend spoor rollen en gemeten met een stopwatch de tijd die het hele spoor kost. 

De meting wordt 11 keer gedaan, met de zorg om de kar van dezelfde plaats vrij te geven, zonder enige impuls te geven en de neiging te houden.

De verkregen set resultaten is:

3,12S 3.09S 3.04S 3.04S 3.10S 3.08S 3.05S 3.10S 3.11s 3.06S, 3.03S

Wat is de willekeurige fout van de maatregelen?

Figuur 4. De tijd nemen van een speelgoedstrolle die afdaalt door een hellend vlak. Bron: Fanny Zapata.

Oplossing

Zoals te zien is, zijn de verkregen resultaten niet uniek en variëren ze enigszins.

De eerste is om de gemiddelde daaltijdwaarde te berekenen en 3,074545455 seconden te verkrijgen.

Het heeft geen zin om zoveel decimalen te handhaven, omdat elke meting drie significante cijfers heeft en de tweede decimaal van elke maatregel onzeker is, omdat deze op de limiet van waardering van de stopwatch is, daarom wordt het resultaat afgerond op twee decimalen:

= 3,08 s.

Met de rekenmachine in de statistische modus is de standaardafwijking σ = 0,03 s En de standaardfout is σ / √11 = 0,01 s. Het eindresultaat wordt als volgt uitgedrukt:

Afdalingstijd 

3,08 s ± 0,01s (met een betrouwbaarheidsniveau van 68%)

3,08 s ± 0,02s (met een betrouwbaarheidsniveau van 95%)

3,08 s ± 0,03s (met een betrouwbaarheidsniveau van 99,7%)

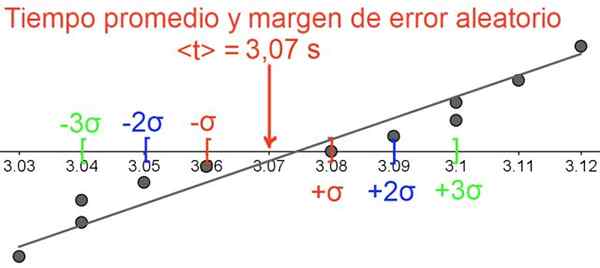Figuur 5. De willekeurige foutmarge, merk op dat de gegevens zijn gegroepeerd rond de gemiddelde waarde. Bron: f. Zapata.

Referenties

1. Canavos, G. 1988. Waarschijnlijkheid en statistieken: toepassingen en methoden. McGraw Hill.
2. Devore, J. 2012. Waarschijnlijkheid en statistieken voor engineering en wetenschap. 8e. Editie. Hekelen.
3. Helmestine a. Willekeurige fout versus. Systematische fout. Hersteld van: Thoughtco.com
4. Laredo, E. Middelste fouten. Hersteld van: USB.gaan.
5. Levin, r. 1988. Statistieken voor beheerders. 2e. Editie. Prentice Hall.