Bepaling van translationele balans, toepassingen, voorbeelden

Hij Translationele balans Het is een toestand waarin een object als geheel is wanneer alle krachten die erop werken worden gecompenseerd, wat resulteert in een leegte. Wiskundig is het gelijkwaardig aan te zeggen dat f₁+ F₂ +  F₃ +.. . = 0, F zijn₁, F₂,  F₃... de betrokken krachten.

Het feit dat een lichaam zich in translationeel evenwicht bevindt, betekent niet dat het noodzakelijkerwijs in rust is. Dit is een bepaald geval van de vorige definitie. Het object kan in beweging zijn, maar bij afwezigheid van versnelling is dit een uniforme rechtlijnige beweging.

Figuur 1. De vertaalbalans is belangrijk voor een groot aantal sporten. Bron: Pixabay.

Dus als het lichaam in rust is, gaat door. En als je al beweging hebt, zal het een constante snelheid hebben. Over het algemeen is de beweging van elk object een samenstelling van vertalingen en rotaties. Vertalingen kunnen zijn zoals getoond in figuur 2: lineair of kromlijnig.

Maar als een van de punten van het object is vastgesteld, is de enige mogelijkheid om te bewegen om te roteren. Voorbeeld hiervan is een CD, waarvan het centrum is vastgesteld. De CD heeft de mogelijkheid om rond een as te roteren die door dat punt passeert, maar niet om te bewegen.

Wanneer objecten vaste punten hebben of op oppervlakken worden ondersteund, is er sprake van links. De links werken op elkaar om de bewegingen te beperken die het object kan maken.

[TOC]

Bepaling van het translationele evenwicht

Voor een evenwichts deeltje is het geldig om ervoor te zorgen dat:

F_R = 0

Of Samenvattende notatie:

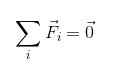
Het is duidelijk dat om een ​​lichaam in translationeel evenwicht te zijn, de krachten die erop werken op een of andere manier worden gecompenseerd, zodat het resultaat nietig is.

Op deze manier zal het object geen versnelling ervaren en zijn al zijn deeltjes in rust of experimen ze rechtlijnige vertalingen met constante snelheid.

Het kan u van dienst zijn: theorie van de oerknal: kenmerken, fasen, bewijs, problemen

Nu, als objecten kunnen draaien, zullen ze het meestal doen. Daarom bestaan ​​de meeste bewegingen uit vertaal- en rotatiecombinaties.

Rotatie van een object

Wanneer de rotatiebalans belangrijk is, kan het nodig zijn om ervoor te zorgen dat het object niet draait. Dan moet je bestuderen of er mes of momenten zijn die erop handelen.

Het koppel is de vectorgrootte waarop de rotaties afhangen. Vereist dat een kracht wordt toegepast, maar het toepassingspunt hiervan is ook belangrijk. Overweeg een uitgebreid object waarop een kracht handelt om het idee te verduidelijken F En laten we kijken of u een rotatie kunt produceren ten opzichte van een as of.

Het is al intuïtief dat door het object op punt P met de kracht te duwen F, Het is mogelijk om de punt O om te draaien, met een anti -horaire richting. Maar de richting waarin kracht wordt uitgeoefend is ook belangrijk. De kracht die in de figuur van het medium wordt uitgeoefend, kan bijvoorbeeld het object niet omdraaien, hoewel het het zeker kan verplaatsen.

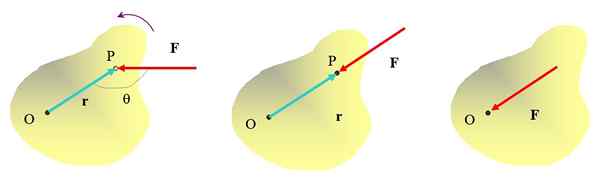Figuur 2. Verschillende manieren om een ​​kracht toe te passen op een uitgebreid object, alleen in de figuur van het uiterste links wordt een rotatie -effect verkregen. Bron: zelf gemaakt.

Breng kracht rechtstreeks op het punt aan of wordt ook niet gebruikt om het object te draaien. Dan is het duidelijk dat om een ​​rotatie -effect te bereiken, de kracht moet worden uitgeoefend op een bepaalde afstand van de rotatieas en de werklijn niet door die as mag gaan.

Definitie van koppel

Het koppel of het moment van een kracht, aangeduid als τ de vectorgrootte die verantwoordelijk is voor het samenstellen van al deze feiten, wordt gedefinieerd als:

τ = r X F

De vector R Het is gericht vanaf de rotatieas tot het toepassingspunt van de kracht en de deelname van de hoek tussen R en F is belangrijk. Daarom wordt de grootte van het koppel uitgedrukt als:

Kan u van dienst zijn: Newton's eerste wet: formules, experimenten en oefeningen

τ = r.F.Sen Q

Het meest effectieve koppel vindt plaats wanneer R En F Ze staan ​​loodrecht.

Nu, als er gewenst is dat er geen rotaties of deze passeren met constante hoekversnelling, is het noodzakelijk dat de som van de knooppunten die op het object werken nietig is, analoog aan wat voor de krachten werd overwogen:

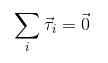
Evenwichtsvoorwaarden

Balans betekent stabiliteit, harmonie en evenwicht. Om de beweging van een object deze kenmerken te laten bezitten, moeten de in de vorige secties beschreven voorwaarden worden toegepast:

1) f₁+ F₂ +  F₃ +.. . = 0

2) τ₁+ τ₂ +  τ₃ +.. . = 0

De eerste voorwaarde garandeert het translationele evenwicht en de tweede de rotatie. Beide moeten worden vervuld als het object erin wil blijven statisch evenwicht (Afwezigheid van welke aard dan ook).

Toepassingen

De evenwichtsvoorwaarden zijn van toepassing op tal van structuren, omdat wanneer gebouwen of diverse objecten worden gebouwd, het wordt gemaakt met de bedoeling dat hun onderdelen in dezelfde relatieve posities met elkaar worden gehandhaafd. Met andere woorden, dat het object niet wordt ontwapend.

Dit is bijvoorbeeld belangrijk bij het bouwen van bruggen die stevig onder hun voeten blijven, of bij het ontwerpen van bewoonbare structuren die niet van positie veranderen of de neiging hebben om te dumpen.

Hoewel wordt aangenomen dat de uniforme rechtlijnige beweging een extreme vereenvoudiging is van de beweging, die meestal weinig in de natuur voorkomt, moet worden herinnerd dat de snelheid van het licht in de leegte constant is, en die van het geluid in de lucht ook, als beschouwt homogeen voor het milieu.

In veel mobiele structuren gemaakt door de mens is het belangrijk dat een constante snelheid wordt gehandhaafd: bijvoorbeeld op mechanische trappen en assemblagelijnen.

Het kan u van dienst zijn: tweede wet van thermodynamica: formules, vergelijkingen, voorbeelden

Voorbeelden van translationele evenwicht

Dit is de klassieke uitoefening van spanningen die de lamp in evenwicht houden. Het is bekend dat de lamp 15 kg weegt. Vind de grootten van de benodigde spanningen om het in deze positie te houden.

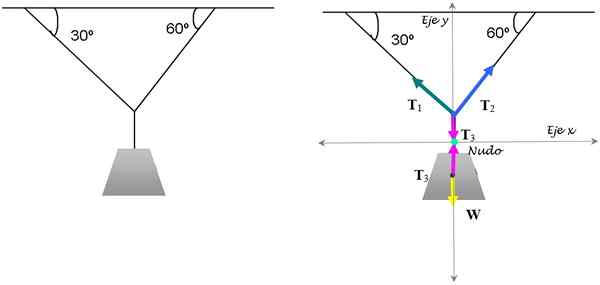figuur 3. De lampbalans wordt gegarandeerd door de translationele balansconditie toe te passen. Bron: zelf gemaakt.

Oplossing

Om het op te lossen, concentreren we ons op de knoop waar de drie snaren samenkomen. De respectieve vrije lichaamsdiagrammen voor de knoop en voor de lamp worden in de bovenstaande figuur weergegeven.

Het gewicht van de lamp is W = 5 kg . 9.8 m/s² = 49 n. Om de lamp in balans te hebben, is het voldoende dat aan de eerste balansconditie wordt voldaan:

T₃ - W = 0

T₃ = W = 49 n.

Spanningen T₁ En T₂ Ze moeten ontbinden:

T_1y + T_{2 en} - T₃ = 0 (Zomer van krachten langs de y -as))

-T_1x +T_2x = 0 (Zomer van krachten langs de X -as)

Trigonometrie toepassen:

T₁.Cos 60º +T₂ .Cos 30º = 49

- T₁.Sen60º +T₂.Sen30º = 0

Het is een systeem van twee vergelijkingen met twee onbekenden, wiens antwoord is: T₁ = 24.5 n En T₂ = 42.4 n.

Referenties

1. Rex, a. 2011. Fundamentals of Physics. Pearson. 76 - 90.
2. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7^ma. ED. Cengage leren. 120 - 124.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^NA ED. Cengage leren. 99-112.
4. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. MacGraw Hill. 71 - 87.
5. Walker, J. 2010. Natuurkunde. Addison Wesley. 332 -346.