Potentiële energiekarakteristieken, typen, berekening en voorbeelden

De potentiële energie Het is de energie die de lichamen hebben onder hun configuratie. Wanneer objecten op elkaar inwerken, zijn er krachten die kunnen werken, en dit vermogen om werk te doen, dat wordt opgeslagen in de beschikking die ze hebben, kan zich vertalen in energie.

Mensen hebben bijvoorbeeld gebruik gemaakt van de potentiële energie van water sinds onheuglijke tijden, eerste spinmolens en vervolgens in hydro -elektrische planten.

Niagara Falls: een enorm zwaartekracht potentieel energiereserve. Bron: Pixabay.

Aan de andere kant hebben veel materialen een opmerkelijk vermogen om werk te doen door te vervormen en vervolgens terug te keren naar de oorspronkelijke grootte. En in andere omstandigheden maakt de opstelling van de elektrische lading mogelijk om elektrische potentiële energie op te slaan, zoals in een condensor.

Potentiële energie biedt veel mogelijkheden om te transformeren in andere nuttige vormen van energie, vandaar het belang van het kennen van de wetten die het regeren. 

[TOC]

Oorsprong van potentiële energie

De potentiële energie van een object heeft zijn oorsprong in de krachten die dit beïnvloeden. Potentiële energie is echter een scalaire omvang, terwijl krachten vector zijn. Om de potentiële energie te specificeren, is het daarom voldoende om de numerieke waarde en de geselecteerde eenheden aan te geven.

Een andere belangrijke kwaliteit is het type kracht waarmee potentiële energie kan worden opgeslagen, omdat geen enkele kracht deze deugd heeft. Alleen conservatieve krachten slaan potentiële energie op in de systemen waarop ze handelen.

Een conservatieve kracht is dat waarvoor het werk niet afhangt van het traject gevolgd door het object, maar alleen van het startpunt en het aankomstpunt. De kracht die water drijft, is de zwaartekracht, wat een conservatieve kracht is.

Aan de andere kant bezitten elastische en elektrostatische krachten ook deze kwaliteit, daarom is er potentiële energie bij hen geassocieerd.

Krachten die niet voldoen aan de bovengenoemde vereiste, ze worden niet -conservatief genoemd; Voorbeeld van hen zijn in wrijving en luchtweerstand.

Soorten potentiële energie

Aangezien potentiële energie altijd afkomstig is van conservatieve krachten zoals al genoemde, is er sprake van zwaartekrachtpotentiaalergie, elektrostatische potentiële energie, nucleaire potentiële energie en potentiële energiechemische energie.

Gravitationele potentieel energie

Elk object heeft potentiële energie op basis van de hoogte die ze hebben met betrekking tot de grond. Dit simpele feit in uiterlijk, illustreert omdat de waterval in staat is om turbines te stimuleren en uiteindelijk wordt omgezet in elektriciteit. Het voorbeeld van de hier getoonde skiërs toont ook de relatie tussen gewicht en lengte met zwaartekrachtpotentiaal energie.

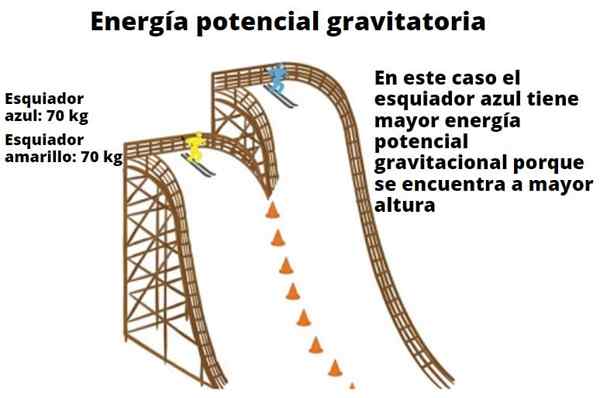
Een ander voorbeeld is dat van een roller bergauto, die een grotere potentiële energie heeft wanneer deze op een bepaalde hoogte op de grond is. Zodra het het niveau van de vloer heeft bereikt, is de hoogte gelijk aan nul en is al zijn potentiële energie omgezet in kinetische energie (bewegingsenergie).

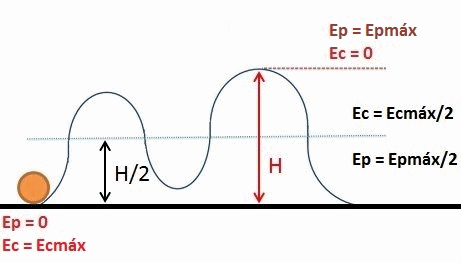Animatie toont de uitwisseling tussen zwaartekrachtpotentiaal energie en kinetische energie, van een object dat op een achtbaan beweegt. De som van beide energieën, mechanische energie genoemd, is constant gedurende de beweging. Bron: Wikimedia Commons.

Elastische potentiële energie

Objecten zoals bronnen, bogen, kruisbogen en competities zijn in staat om elastische potentiële energie op te slaan.

Wanneer de boog gespannen is, doet de doelman een werk die wordt opgeslagen als potentiële energie van het boog-fet-systeem. Wanneer de boog wordt afgegeven, wordt deze energie omgezet in beweging van de pijl. Bron: Pixabay.

De elasticiteit van een lichaam of een materiaal wordt beschreven door de wet van Hooke (tot bepaalde grenzen), die ons vertelt dat de kracht die kan uitoefenen wanneer ze worden uitgeoefend of uitgerekt, evenredig is met de vervorming ervan.

Kan u van dienst zijn: ferromagnetisme: materialen, toepassingen en voorbeelden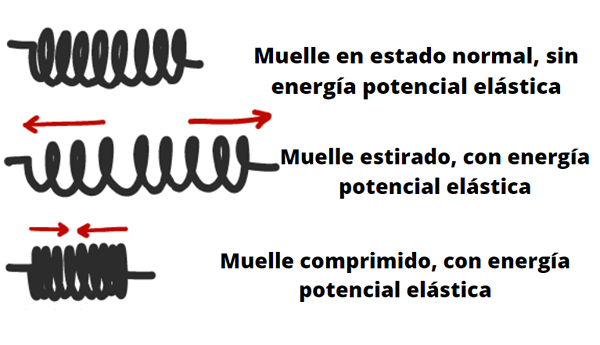

Bijvoorbeeld in het geval van een veer of veer, betekent dit dat hoe meer het krimpt of zich uitstrekt, hoe groter de kracht die kan worden uitgeoefend op een object dat aan één uiteinde is geplaatst.

Elektrostatische potentiële energie

Het is de energie die elektrische ladingen hebben onder hun configuratie. De elektrische ladingen van hetzelfde teken worden afgestoten, dus om een ​​paar positieve belastingen - of negatief - in een bepaalde positie te plaatsen, moet een extern middel werk doen. Anders zouden ze de neiging hebben om te scheiden.

Dit werk wordt opgeslagen in de manier waarop de ladingen zich bevonden. Hoe dichter de belastingen van hetzelfde teken zijn, hoe groter de potentiële energie die de configuratie zal hebben. Het gebeurt integendeel als het gaat om verschillende tekenen ladingen; Terwijl ze aantrekken, hoe dichter ze zijn, hoe minder potentiële energie ze hebben.

Nucleair potentieel energie

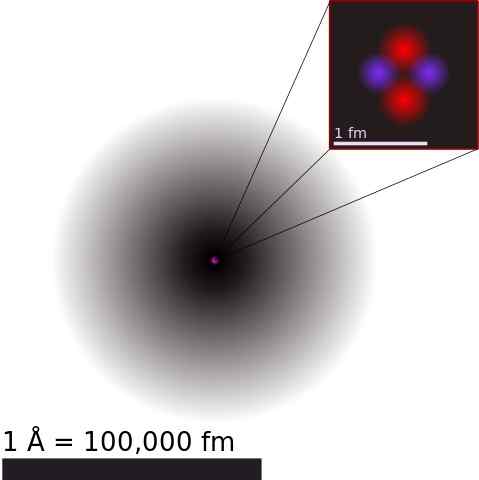Geschatte heliumatoom. In de kern worden de protonen in rood weergegeven en de neutronen in het blauw.

De atoomkern bestaat uit protonen en neutronen, algemeen genoemd Nucleones. De eerste hebben een positieve elektrische lading en de laatste zijn neutraal.

Omdat ze worden geagglomereerd in een kleine ruimte voorbij de verbeelding, en wetende dat de ladingen van hetzelfde teken zijn afgestoten, is het de moeite waard om te vragen hoe de atoomkern samenhangend blijft.

Het antwoord is in andere krachten naast elektrostatische afstoting, typisch voor de kern, zoals sterke nucleaire interactie en zwakke nucleaire interactie. Dit zijn zeer intense krachten, die de elektrostatische kracht ver overschrijden.

Chemische potentiële energie

Deze vorm van potentiële energie komt van hoe atomen en stoffen moleculen beschikbaar zijn, volgens de verschillende soorten chemische bindingen.

Wanneer een chemische reactie wordt gegeven, kan deze energie worden omgezet in andere typen, bijvoorbeeld door een elektrische batterij of batterij.

Voorbeelden van potentiële energie

Potentiële energie is in veel aspecten aanwezig in het dagelijks leven. Het observeren van de effecten is net zo eenvoudig als het plaatsen van elk object op een bepaalde hoogte en de zekerheid hebben dat het op elk gewenst moment kan rollen of vallen.

Hier zijn enkele manifestaties van de eerder beschreven potentiële energietypen:

-Achtbanen

-Auto's of ballen rollen bergafwaarts

-Pijlen en bogen

-Elektrische batterijen

-Een klokslander

Wanneer een van de extreme bollen in beweging wordt gezet, wordt de beweging overgedragen aan de anderen. Bron: Pixabay.

-Slingeren in een schommel

-Uitgestrekt

-Gebruik een intrekbare pen.

Zie: Voorbeelden van potentiële energie.

Potentiële energieberekening

De potentiële energie hangt af van het werk dat kracht maakt en dit hangt op zijn beurt niet af van het traject, dan kan worden bevestigd dat:

-Als A en B twee punten zijn, het werk W_Aab  nodig om van A naar B te gaan, het is gelijk aan het benodigde werk om van B naar een te gaan. Daarom: W_Aab = W_Ba, Dus:

W_Aab + W_Ba = 0

-En als twee verschillende trajecten 1 en 2 worden getest om lid te worden van deze punten A en B, is het werk dat in beide gevallen wordt gedaan ook hetzelfde:

 W₁ = W₂.

In elk geval ervaart het object een verandering in potentiële energie:

Verandering = uiteindelijke potentiële energie - initiële potentiële energie

Δu = u_laatste - OF_voorletter = U_B - OF_NAAR

Welnu, de potentiële energie van het object wordt gedefinieerd als het negatieve van het werk dat door geweld wordt uitgevoerd (conservatief):

Δu = -w_Aab

Maar omdat werk wordt bepaald door deze integraal:

Kan u van dienst zijn: de 31 soorten kracht in de natuurkunde en hun kenmerken

Waar F En DR (met vetgedrukte of pijl aan) zijn respectievelijk de sterkte- en verplaatsingsvectoren. Met dit in gedachten is de verandering in potentiële energie het negatieve van deze integraal:

Voor conservatieve krachten zoals beschreven, wordt de integraal gemakkelijk berekend. 

Merk op dat de eenheden van potentiële energie hetzelfde zijn als die van werk. In het internationale systeem als de eenheid de joule is, die is afgekort en gelijkwaardig aan 1 Newton X Metro, Door de Engelse natuurkundige James Joule (1818-1889).

Andere eenheden voor energie zijn de Ergio in het CGS-systeem, de pond-fork x voet, de BTU (Britse Warmte-eenheid), calorieën en kilowatt-hora.

Laten we enkele specifieke gevallen bekijken van het berekenen van potentiële energie.

Berekening van zwaartekrachtpotentiaal energie

In de buurt van het aardoppervlak wijst de kracht van zwaartekracht verticaal naar beneden en wordt de grootte ervan gegeven door de vergelijking Gewicht = massa x zwaartekracht.

De verticale as aanduiden met de letter "y" en het toewijzen van dit adres de eenheidsvector J, positief en negatief naar beneden, de verandering in potentiële energie wanneer een lichaam van beweegt y = y_NAAR tot y = y_B is:

Waar M vertegenwoordigt het lichaam van het lichaam en G De waarde van de versnelling van de zwaartekracht. Als u wordt gekozen en_NAAR = 0 Als referentieniveau op de grond, waarin u is vastgesteld als 0, hebt u:

U (y) = mgy

Berekening van elastische potentiële energie

De wet van Hooke vertelt ons dat kracht evenredig is met vervorming:

F = -k.X

Hier X Het is de vervorming en k Het is een constante van de veer, wat aangeeft hoe rigide het is. Door deze uitdrukking wordt elastische potentiële energie berekend, rekening houdend met dat Je Het is de eenheidsvector in de horizontale richting:

Bij het kiezen OF_NAAR = 0 in  X_NAAR, De vorige uitdrukking is de functie U (x) Voor de potentiële energie van de lente:

U (x) = ½ kx²

Elektrostatische potentiële energieberekening

Wanneer u een punctuele elektrische lading heeft, produceert dit een elektrisch veld dat een andere punctuele belasting waarneemt Q, En wat werkt eraan wanneer je van de ene positie naar de andere gaat in het midden van het veld. De elektrostatische kracht tussen twee specifieke belastingen heeft radiale richting, gesymboliseerd door de eenheidsvector R:

 Hier k_En Het is de elektrostatische of constante constante van Coulomb, waarvan de waarde is k_En ≈ 9 x 10⁹  N.M² /C² In internationale systeemeenheden. Het volgt dat:

 U = 0 selecteren wanneer r_NAAR → ∞, blijft:

Opgeloste oefeningen

- Oefening 1: een veer die zich uitstrekt

Een veer waarvan de constante is k = 10.0 n/cm strekt zich in eerste instantie uit 1.00 cm van zijn evenwichtslengte. Er wordt gevraagd om de extra energie te berekenen die nodig is om de veer tot 5 te strekken.00 cm voorbij de lengte van het evenwicht.

Oplossing 

Direct x = 1 vervangen.00 cm in de vergelijking voor u (x).CM, maar centimeters moeten meters worden om energie te verkrijgen in joules:

U (1) = 0.5 x 10.0 n/cm x (1.00 cm)² = 5 n. cm = 0.05 J; U (5) = 0.5 x 10.0 n/cm x (5.00 cm)² = 125 n.cm = 1.25 J

Daarom is het gezochte verschil in energie 1.25 - 0.05 J = 1.20 J.

- Oefening 2: conservatieve en niet -conservatieve krachten

Een klein blok van punt A komt vrij uit rust, zodat het zonder wrijving langs de gebogen helling glijdt. Van daaruit komt het een lang ruw horizontaal oppervlak binnen, met een dynamische wrijvingscoëfficiënt μ_k = 0.2. Vind op welke afstand van punt B stopt, ervan uitgaande dat h_NAAR= 3M.

Kan u dienen: Barrada -spiraalvormige sterrenstelsel: vorming, evolutie, kenmerken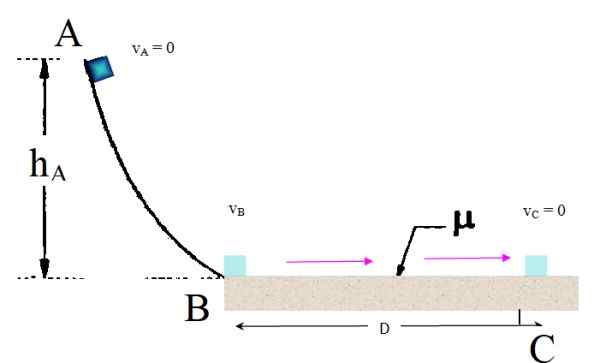Figuur bijvoorbeeld 1. Bron: f. Zapata.

Oplossing 

Wanneer het blok op een hoogte is h_NAAR Wat de vloer betreft, heeft het zwaartekracht potentiële energie vanwege zijn hoogte. Bij het loslaten wordt deze potentiële energie geleidelijk kinetische energie, en terwijl deze door de gladde gebogen helling glijdt, neemt de snelheid toe.

Tijdens de reis van A naar B kunnen de vergelijkingen van de uniform gevarieerde rechtlijnige beweging niet worden toegepast. Hoewel de zwaartekracht verantwoordelijk is voor de beweging van het blok, is de beweging die dit ervaart complexer is, omdat het traject niet rechtlijnig is.

Energiebesparing op de AB -route

Omdat de zwaartekracht echter een conservatieve kracht is en in de helling geen wrijving is, kan het behoud van mechanische energie worden gebruikt om de snelheid te vinden wanneer deze het einde van de helling bereikt:

Mechanische energie bij A = mechanische energie in B

M.G.H_NAAR + ½ m.v_NAAR² = m.G.H_B + ½ m.v_B²

De uitdrukking wordt vereenvoudigd door op te merken dat de massa in elke term verschijnt. Wordt vrijgelaten uit Rest V_NAAR = 0. En h_B Het is op grondniveau, h_B = 0. Met deze vereenvoudigingen wordt de uitdrukking gereduceerd tot:

v_B² = GH_NAAR

Werk gedaan door te wrijven in sectie BC

Nu begint het blok met deze snelheid zijn route in het ruwe gedeelte en stopt uiteindelijk op punt C. Daarom V_C = 0. Mechanische energie wordt niet langer bewaard, omdat wrijving een dissipatieve kracht is, die een werk heeft verricht op het blok gegeven door:

W_aanraken = -Frue van wrijving x afgelegde afstand

Dit werk heeft een negatief teken, omdat kinetische wrijving vertraagt ​​naar het object, tegen zijn beweging. De omvang van kinetische wrijving F_k  is:

F_k = μ_k .N

Waarbij n de omvang van de normale kracht is. De normale kracht wordt uitgeoefend door het oppervlak op het blok en omdat het oppervlak volledig horizontaal is, omdat het het gewicht in evenwicht houdt P = mg, Daarom is de omvang van het normaal:

N = mg

Wat leidt tot:

F_k = μ_k .mg

Het werk dat F_k Maakt op het blok is: W_k = - f_k .D =- μ_k .mg.D.

Berekening van verandering in mechanische energie

Dit werk is gelijk aan de verandering in mechanische energie, berekend als volgt:

Mechanische energie in C - mechanische energie bij B =

ΔE_M = (U_C +K_C)- (OF_B + K_B) = - μ_k .mg.D

In deze vergelijking zijn er enkele termen die nietig zijn: K_C = 0, omdat het blok stopt in C en ook niet wordt geannuleerd_C = U_B, om deze punten op de grondniveau te zijn. Vereenvoudiging resulteert in:

- K_B = - μ_k .M.G.D

½ m.v_B² = μ_k .M.G.D

Het deeg wordt opnieuw geannuleerd en kan als volgt worden verkregen:

D = (½ V_B²)/(μ_k . G) = (½ V_B²)/(μ_k . g) = (½ g.H_NAAR)/(μ_k . g) = (½h_NAAR)/μ_k = 0.5 x 3 m / 0.2 = 7.5m

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 2. Dynamisch. Uitgegeven door Douglas Figueroa (USB).
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
4. Ridder, r.  2017. Fysica voor wetenschappers en engineering: een strategiebenadering. Pearson. 
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1-2.