Helmholtz vrije energie -eenheden, hoe het wordt berekend, opgeloste oefeningen

De Helmholtz gratis energie Het is een thermodynamisch potentieel dat het nuttige werk van een gesloten systeem meet in constante temperatuur- en volumecondities. Helmholtz's vrije energie wordt aangeduid als F En het wordt gedefinieerd als het verschil met interne energie OF Minder het temperatuurproduct T Voor entropie S:

F = u - t⋅s

Omdat het energie is, wordt het gemeten in joules in het International System (SI), hoewel andere geschikte eenheden ook Ergios (CGS), calorieën of elektronenvolt kunnen zijn (EV).

Figuur 1. Definitie van de energie van Helmholtz. Bron: Pixabay.

De negatieve variatie van de energie van Helmholtz tijdens een proces wordt gelijkgesteld met het maximale werk dat het systeem kan uitvoeren in een isocorisch proces, dat wil zeggen tot constant volume. Wanneer het volume niet constant is, kan een deel van dit werk aan de omgeving worden gedaan.

In dit geval verwijzen we naar werk waarin het volume niet varieert, zoals elektrisch werk: dw = φdq, met φ als de elektrische potentiaal en q als elektrische lading.

Als de temperatuur ook constant is, wordt de energie van Helmholtz geminimaliseerd wanneer de balans wordt bereikt. Voor dit alles is de energie van Helmholtz bijzonder nuttig in constante volumeprocessen. In dit geval heb je:

- Voor een spontaan proces: Δf < 0

- Wanneer het systeem in evenwicht is: Δf = 0

- In een niet-spontaan proces: Δf> 0.

[TOC]

Hoe wordt Helmholtz vrije energie berekend??

Zoals in het begin wordt vermeld, wordt de energie van Helmholtz gedefinieerd als "de interne energie of het systeem, behalve het product van het systeem absolute T -temperatuur, door de entropie S van het systeem":

F = u - t⋅s

Het is een functie van de temperatuur T en Volume V. De stappen om dit te visualiseren zijn de volgende:

Kan u van dienst zijn: interne elektronen

- Beginnend met de eerste wet van de thermodynamica, interne energie of is gerelateerd aan de entropie S van het systeem en zijn volume V voor omkeerbare processen via de volgende differentiële relatie:

Du = DQ - DW = TDS - PDV

Hieruit volgt dat interne energie of een functie van variabelen is S En V, daarom:

U = u (s, v)

- Nu de definitie van F En het is afgeleid:

df = du - d (ts) = du - tds - sdt

- De differentiële expressie die in de eerste stap is verkregen, blijft daar de differentiële uitdrukking vervangen:

DF = TDS - PDV - TDS - SDT = -SDT - PDV

- Ten slotte wordt geconcludeerd dat F een functie is van de temperatuur T en volume V en kan worden uitgedrukt als:

F = f (t, v)

Figuur 2. Hermann von Helmholtz (1821-1894), Duitse fysicus en arts, erkend voor zijn bijdragen aan elektromagnetisme en thermodynamica, onder andere wetenschapsgebieden. Bron: Wikimedia Commons.

Spontane processen

De energie van Helmholtz kan worden toegepast als een algemeen criterium van spontaniteit in geïsoleerde systemen, maar voordat sommige concepten moeten worden gespecificeerd:

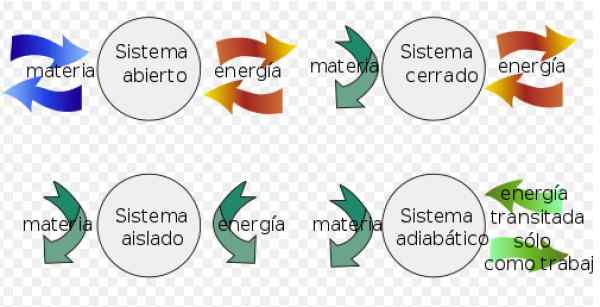
- A Systeem gesloten Het kan energie uitwisselen met het milieu, maar kan materie niet uitwisselen.

- In plaats daarvan een geïsoleerd systeem Wisselt geen materie of energie uit met de omgeving.

- Eindelijk een open systeem Wissel materie en energie uit met de omgeving. 

figuur 3. Thermodynamische systemen. Bron: Wikimedia Commons. Fjgar (bis) [cc by-sa (https: // creativeCommons.Org/licenties/by-sa/4.0)].

In omkeerbare processen wordt de variatie in interne energie als volgt berekend:

DU = TDS - PDV

Stel nu een constant volume (isocorisch) proces, waarin de tweede term van de vorige uitdrukking een nulbijdrage heeft. Er moet ook aan worden herinnerd dat volgens de Clausius ongelijkheid: 

DS ≥ DQ/T

Een dergelijke ongelijkheid is van toepassing op een geïsoleerd thermodynamisch systeem.

Zodat voor een proces (omkeerbaar of niet) waarin het volume constant wordt gehandhaafd, wordt vervuld:

Kan u van dienst zijn: fosforzuur (H3PO4)

T ds ≥ du (Bij vast volume)

Overwegende dat:

df = du - t ds 

We zullen in een isocorisch proces bij constante temperatuur moeten worden vervuld die: DF ≤ 0, Zoals in het begin aangegeven.

Zodat de energie van Helmholtz F een afnemende hoeveelheid is in een spontaan proces, terwijl het een geïsoleerd systeem is. F bereikt zijn minimale en stabiele waarde wanneer omkeerbare balans is bereikt.

Opgeloste oefeningen

Oefening 1

Bereken de variatie van de vrije energie van Helmholtz F voor 2 mol ideaal gas bij een temperatuur van 300K tijdens een isotherme expansie die leidt tot het systeem van een initiële volume van 20 liter tot een eindvolume van 40 liter.

Oplossing

Beginnend bij de definitie van f:

F = u - t s

Dan zal een eindige variatie van F, Δf genoemd, zijn:

Δf = Δu - t δs

Zoals de verklaring stelt dat de temperatuur constant is: Δt = 0. In ideale gassen hangt interne energie echter alleen af ​​van de absolute temperatuur, maar omdat het een isotherme proces is, dan Δu = 0 En Δf = - T ΔS. Voor ideale gassen is de entropievariatie van een isotherme proces als volgt geschreven: 

Δs = n.R.ln (v₂/V₁))

Deze uitdrukking toepassen:

ΔS = 2 mol x 8,314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Ten slotte is de verandering in de energie van Helmholtz:

Δf = - t δs = - 300k x 11,53 j/k = -3457.70 j.

Oefening 2

In een cilinder is er een zuiger die deze in twee secties verdeelt en aan elke kant van de zuiger zijn er N mol een ideaal monoatomisch gas, zoals getoond in de onderstaande figuur.

De cilinderwanden zijn goede warmtegeleiders (diathermiek) en hebben contact met een T -temperatuurreservoir_of.

Het initiële volume van elk van de cilindersecties zijn V_1i en v_2i, terwijl de laatste delen V zijn_1F en v_2F Na een eigenste verplaatsing. De zuiger beweegt door middel van een zuiger die hermetisch de twee cilindertapas kruist.

Het kan u van dienst zijn: Tecnecio (TC): structuur, eigenschappen, gebruik, verkrijgen

Er wordt gevraagd om te vinden:

a) De verandering in de interne gasergie en het werk van het systeem en

b) de energievariatie van Helmholtz.

Oplossing voor

Naarmate de zuiger onteigenlijk beweegt, moet de externe kracht die op de plunjer wordt uitgeoefend de kracht in evenwicht brengen vanwege het drukverschil in de twee secties van de cilinder.

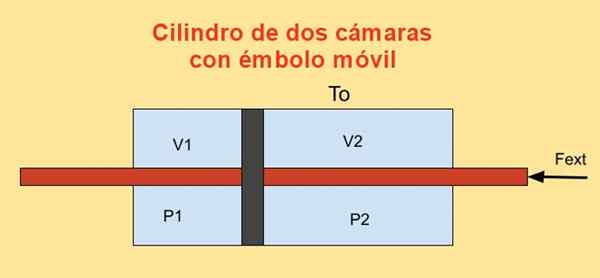Figuur 4. Variatie van vrije energie F in een cilinder met twee camera's. Bron: f. Zapata.

De baan DW Gemaakt door externe kracht F_ext Tijdens een oneindige verplaatsing Dx is:

DW = - F_ext Dx = (p₁ - P₂) A dx = p₁ Dv₁ + P₂ Dv₂

Waar de relatie is gebruikt Dv₁ = - DV₂ = A DX, wezen naar Het zuiger gebied. Aan de andere kant is de variatie van de energie van Helmholtz: 

DF = -SDT - PDV

Omdat tijdens het proces de temperatuur niet verandert, dan dt = 0 En DF = - PDV. Deze uitdrukking toepassen op elke sectie van de cilinder die u hebt:

DW = P₁ Dv₁ + P₂ Dv₂ = - DF₁ - DF₂

Wezen F₁  En F₂ Helmholtz's energieën in elk van de camera's.

Eindige W -werk kan worden berekend uit de eindige variatie van Helmholtz's energie van elke camera:

W = -Af₁ - Δf₂

Oplossing B

Om de verandering van energie van Helmholtz te vinden, wordt de definitie gebruikt: F = u - t s. Zoals in elke camera heb je een ideaal monoatomisch gas bij constante temperatuur T_of, Interne energie verandert niet (Δu = 0), zodat: Δf = - t_of Δs. Daarnaast:

ΔS = nr ln (v_F/Zaag)

Dat door het te vervangen, het werk eindelijk mogelijk maakt, is: 

W = -t_of Nr ln (v_1F /V_1i) -To nr ln (v_2F /V_2i) = -Af₁ -Δf₂

W = - tot nr ln [(v_1F ⋅ v_1i)/(V_{2F .}V_2i)] = - Δf_totaal

Wezen Δf_totaal De totale variatie van de energie van Helmholtz.

Referenties

1. Castaños e. Gratis energie -oefeningen. Hersteld van: Lidiaconlachimica.WordPress.com
2. Librhetxts. Helmholtz Energy. Hersteld van: chem.Librhetxts.borg
3. Librhetxts. Wat zijn gratis energie. Hersteld van: chem.Librhetxts.borg
4. Wikipedia. Helmholtz Energy. Hersteld van: is.Wikipedia.com
5. Wikipedia. Helmholtz gratis energie. Opgehaald uit: in.Wikipedia.com