Gibbs vrije energie -eenheden, hoe het wordt berekend, opgeloste oefeningen

De Gibbs gratis energie (gewoonlijk G) genoemd is een thermodynamisch potentieel gedefinieerd als het verschil in enthalpie H, behalve het product van de temperatuur T, door de entropie S van het systeem:

G = h - t s

Gibbs Free Energy wordt gemeten in Joules (volgens het internationale systeem), in Ergios (voor het competitiesysteem van eenheden), in calorieën of elektronenvolt (Voor electro -volt).

Figuur 1. Diagram die de definitie van Gibbs -energie en zijn relatie met de andere thermodynamische potentialen toont. Bron: nucleaire kracht.netto.

In de processen die optreden bij constante druk en temperatuur, is de variatie van Gibbs -vrije energie Δg = ΔH - t δs. In dergelijke processen vertegenwoordigt (g) de beschikbare energie in het systeem dat werk kan worden.

Bij exotherme chemische reacties neemt de enthalpie bijvoorbeeld af terwijl de entropie toeneemt. In de Gibbs -functie worden deze twee factoren tegengegaan, maar alleen wanneer de Gibbs -energie de reactie afneemt, vindt het spontaan plaats.

Dus als de variatie van G negatief is, is het proces spontaan. Wanneer de Gibbs -functie het minimum bereikt, bereikt het systeem een ​​stabiel evenwicht. Kortom, in een proces waarvoor druk en temperatuur constant blijven, kunnen we bevestigen:

- Als het proces spontaan is, dan ΔG < 0

- Wanneer het systeem in evenwicht is: ΔG = 0

- In een niet-spontaan proces neemt het toe: ΔG> 0.

[TOC]

Hoe wordt het berekend?

Gibbs Free Energy (G) wordt berekend door de definitie die in het begin wordt gegeven:

G = h - t⋅s

Op zijn beurt is Enthalpy H een thermodynamisch potentieel gedefinieerd als:

H = u + p v

- Stap voor stap

Vervolgens wordt een stap -door -step -analyse gedaan om de onafhankelijke variabelen te kennen waarvan Gibbs Energy een functie is:

1- Van de eerste wet van de thermodynamica is interne energie gerelateerd aan de entropie S van het systeem en zijn volume V voor omkeerbare processen door de differentiële relatie:

Het kan u van dienst zijn: Ethidium Bromide: structuur, eigenschappen, gebruik, toxiciteit

Du = DQ - DW = TDS - PDV

Uit deze vergelijking volgt dat interne energie U een functie is van de variabelen S en V:

U = u (s, v)

2- Vanaf de definitie van H en het nemen van het verschil wordt verkregen:

dh = du + d (p v) = du + vdp + pdv

3- Het vervangen van de uitdrukking voor du verkregen in (1) u moet:

DH = TDS - PDV + VDP + PDV = TDS + VDP

Vanaf hier wordt geconcludeerd dat Enthalpy H afhankelijk is van entropie S en druk P, dat wil zeggen:

H = H (S, P)

4- Nu wordt het totale Gibbs Free Energy Differential berekend om te verkrijgen:

Dg = dh -tds -sdt = tds + vdp -tds -sdt

Waar DH is vervangen door de uitdrukking gevonden in (3).

5- Ten slotte, door te vereenvoudigen, krijgt u: DG = VDP - SDT, Het is duidelijk dat vrije energie G afhankelijk is van de druk en temperatuur t als:

G = g (p, t)

- Maxwell's thermodynamische relaties

Uit de analyse in de vorige sectie volgt hieruit dat de interne energie van een systeem een ​​functie is van entropie en volume:

U = u (s, v)

Dan het verschil van OF zijn:

du = ∂_SU |_V Ds + ∂_VU |_S DV = TDS - PDV

Uit deze uitdrukking in gedeeltelijke derivaten kunnen de zo -aangedane maxwell thermodynamische relaties worden afgeleid. Gedeeltelijke derivaten zijn van toepassing wanneer een functie afhankelijk is van meer dan één variabele en gemakkelijk wordt berekend door de stelling van de volgende sectie toe te passen.

Maxwell's eerste relatie

 ∂_VT |_S = -Mon_SP |_V 

Om deze relatie te bereiken, de Clairaut Stelling - Schwarz op gedeeltelijke derivaten, die het volgende vermeldt:

"De tweede orde gemengde derivaten met de uitgewisselde variabelen zijn hetzelfde, op voorwaarde dat de te afgeleide functies continu en onderscheidbaar zijn".

Maxwell's tweede relatie

Beginnend met wat werd aangetoond in punt 3 van de vorige sectie:

Kan u van dienst zijn: factoren die de oplosbaarheid beïnvloeden

H = H (S, P) en DH = TDS + VDP

Kan worden verkregen:

 ∂_PT |_S = ∂_SV |_P 

Ga op een vergelijkbare manier verder met Gibbs vrije energie G = g (p, t) En met de vrije energie van Helmholtz F = f (t, v) Om de andere twee thermodynamische relaties van Maxwell te verkrijgen. 

Figuur 2. Josiah Gibbs (1839-1903) was een Amerikaanse natuurkundige, chemicus en wiskundige die grote bijdragen heeft geleverd aan de thermodynamica. Bron: Wikimedia Commons.

Maxwell's vier thermodynamische relaties 

1- geassocieerd met interne energie u: ∂_VT |_S = -Mon_SP |_V

2- Degene verkregen van Enthalpy H: ∂_PT |_S = ∂_SV |_P 

3- gerelateerd aan de energie van Helmholtz F: ∂_TP |_V = ∂_VS |_T 

4- Gekoppeld aan de vrije energie van Gibbs G: ∂_TV |_P = -Mon_PS |_T

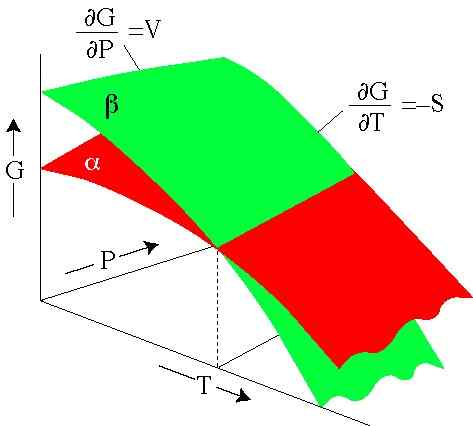Figuur 2. De energie van Gibbs hangt af van druk en temperatuur. Elk oppervlak vertegenwoordigt een fase. (SERC.Carleton.Edu)

Opgeloste oefeningen

Oefening 1

Bereken de variatie van Gibbs -vrije energie voor 2 mol ideaal gas bij een temperatuur van 300K tijdens een isotherme expansie die leidt tot het initiële volumesysteem van 20 liter tot een uiteindelijke volume van 40 liter.

Oplossing

Het onthouden van de definitie van Gibbs -vrije energie is:

G = h - t s

Dan zal een eindige variatie van F zijn:

Δg = ΔH - t δs, Sinds AT = 0

In ideale gassen hangt enthalpie alleen af ​​van zijn absolute temperatuur, maar omdat het een isotherme proces is, dan Δh = 0 en Δg = - t δs.

Voor ideale gassen is de entropievariatie van een isotherme proces: 

ΔS = nr ln (v₂/V₁))

Dat van toepassing was op het geval van deze oefening die we hebben:

ΔS = 2 mol x 8,314 j/(k mol) x ln (40L/20L) = 11,53 j/k

Dan kunnen we de verandering in de energie van Helmholtz krijgen:

ΔG = - 300K x 11.53 J/K = -3457.70 J.

Oefening 2

Rekening houdend met dat Gibbs vrije energie een functie is van temperatuur en druk g = g (t, p); Bepaal de variatie van G tijdens een proces waarin de temperatuur niet verandert (isotherme) voor n mol van een ideaal monoatomisch gas.

Kan u van dienst zijn: strontiumhydroxide (sr (oh) ₂)

Oplossing

Zoals hierboven aangetoond, hangt de verandering in de energie van Gibbs alleen af ​​van de verandering in temperatuur T en volume V, dus een oneindige variatie ervan wordt berekend volgens:

Dg = -sdt + vdp

Maar als het een proces is waarin de temperatuur constant is, dan leidt DF = + VDP, dus een eindige variatie van druk AP leidt tot een verandering in de Gibbs -energie gegeven door:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = + n r t ln (Δp)

Met behulp van de ideale gasvergelijking:

P v = n r t

Tijdens een isothermproces gebeurt het dat:

D (P V) = P DV + V DP = 0

Dat is:

dp/p = - dv/v

Dus het vorige resultaat kan worden geschreven, afhankelijk van de volumevariatie AV:

ΔG = + ∫ vdp = + ∫ (n r t) dp/p = - ∫ (n r t) dv/v = -n r t ln (ΔV)

Oefening 3

Gezien de volgende chemische reactie:

N₂0 (g) + (3/2) of₂ (g) ↔️NO₂ (g) Bij temperatuur T = 298 K

Vind de variatie van Gibbs -vrije energie en geeft door het verkregen resultaat aan of het een spontaan proces is of niet.

Oplossing

Onder de stappen:

- Eerste stap: Reaction Enthalpies

ΔHR = 2*ΔH (nee₂ (g)) - ΔH (n₂0 (g)) = 2*33.2-81.6 = -15.2kj/mol

- Tweede stap: de reactie -entropievariatie

ΔSr = 2*s (nee₂ (g)) - s (n₂0 (g)) - (3/2) s (of₂ (g)) = 2*240.1 - 220.1 - 1.5*205.2 = -47.7 j/(mol*k).

- Derde stap: variatie in de Gibbs -functie

Deze waarde bepaalt de balans tussen afnemende energie en toenemende entropie om te weten of de reactie eindelijk spontaan is of niet.

Δgr = Δhr -t ΔSr = -15.2 -298*(-47.7) = -985.4 j/mol

Omdat het een negatieve variatie van Gibbs -energie is, kan worden geconcludeerd dat het een spontane reactie is bij de temperatuur van 298 k = 25 ºC.

Referenties

1. Castaños e. Gratis energie -oefeningen. Hersteld van: Lidiaconlachimica.WordPress.com.
2. Cengel, en. 2012. Thermodynamica. 7e editie. McGraw Hill.
3. Librhetxts. Gibbs gratis energie. Hersteld van: chem.Librhetxts.borg
4. Librhetxts. Wat zijn gratis energie. Hersteld van: chem.Librhetxts.borg
5. Wikipedia. Gibbs gratis energie. Hersteld van: is.Wikipedia.com
6. Wikipedia. Gibbs gratis energie. Opgehaald uit: in.Wikipedia.com