In welke situaties zijn lineaire en kwadratische functies?

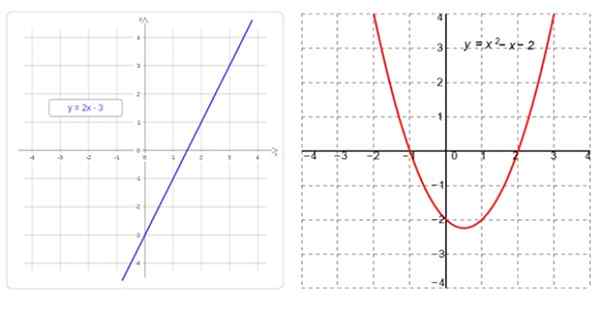
Links een lineaire functie, waarvan de grafiek een rechte lijn is, en rechts een kwadratische functie, waarvan de grafiek een parabool is. Bron: f. Zapata

Wat zijn lineaire en kwadratische functies?

Lineaire functies en kwadratische functies zijn functies die behoren tot de polynoomfunctiesgroep. Ze worden gebruikt om verschillende situaties te modelleren, zoals de afhankelijkheid tussen het volume en het gewicht van een lichaam, de hoeveelheid en kosten van een product, de positie versus tijd en meer.

Over het algemeen is een functie een relatie die twee variabelen verbindt en kan worden gebruikt om de echte wereld te modelleren. Polynoomfuncties, zoals de naam al aangeeft, worden uitgedrukt door een polynoom, wiens algemene vorm is:

f (x) = a_NX^N + naar _N-1X ^N-1 + naar_X-2X^N-2 +… naar_of

Waar n een natuurlijk nummer is, de cijfers om₀, naar₁, naar₂,… naar_N Ze zijn echt, aan₀ Het is de onafhankelijke term en aan_N, Het is de coëfficiënt die gepaard gaat met de hoogste kracht. De waarde van N geeft het type functie aan, voor n = 1 is de functie lineair, terwijl voor n = 2 de functie kwadratisch is.

In de eerste van deze gevallen wordt de algemene uitdrukking gereduceerd tot:

f (x) = a₁x + a_of

En in het tweede geval blijft het zo:

f (x) = a₂X² + naar₁x + a_of ;   (naar₂≠ 0)

De grafieken van de polynoomfuncties zijn continu, dat wil zeggen dat ze geen abrupte sprongen of breuken ervaren, waardoor zacht gedrag zonder onregelmatigheden. Daarom worden ze waargenomen bij het modelleren van vele situaties van wetenschap, economie en andere gebieden van menselijke kennis.

Vervolgens worden interessante toepassingen van elkaar gedetailleerder beschreven.

Situaties waarin lineaire functies verschijnen

De lineaire functie wordt algebraïsch weergegeven door:

f (x) = a₁x + a_of

Of gelijkwaardig:

f (x) = mx + b

Het onderscheidende kenmerk is dat de grafiek een rechte lijn is. De waarde M, dat is de coëfficiënt van de X, vertegenwoordigt de oorbel van deze lijn en geeft een maat voor hoe geneigd het is.

Kan u van dienst zijn: niet -lineaire programmering: methoden en oefeningen

De helling kan positief, negatief of nul zijn, maar het is altijd constant, dat wil zeggen, de wisselkoers blijft ongewijzigd.

Een lijn helling 0 is volledig horizontaal, die van positieve helling duidt op verhoging of toename (als een van de variabelen toeneemt, de andere ook, altijd met dezelfde snelheid) en ten slotte duidt de negatieve helling af (als een van de variabelen neemt toe, de andere neemt af).

De waarde van B, Van zijn kant vertegenwoordigt het de snede of kruising van de lijn met de verticale as. Ja B = 0, De lijn gaat door de oorsprong van het coördinatensysteem.

Modelleringsvoorbeelden met lineaire functies

1. De uniforme rechtlijnige beweging

De vergelijking die de X -positie verbindt en de tijd T van een mobiel, in de uniforme rechtlijnige beweging, is lineair:

x (t) = v⋅t + x_of

Waar V, de helling van de lijn, de snelheid van de mobiel is, die gedurende de hele beweging constant blijft, en x_of is de eerste positie.

2. Dikte

Dichtheid van een object of een stof, die de relatie tussen massa en volume tot stand brengt. P ρ naar de dichtheid bellen (het leest "Rho"), M naar het deeg en V naar het volume, je hebt:

Het deeg vrijmaken, in termen van het volume, wordt het verkregen:

M = ρv

Bij het in de loop van het deeg, afhankelijk van het volume, wordt een rechte lijn verkregen waarvan de helling de dichtheid van het object of de substantie is.

3. Lengte van een omtrek

De contour van een cirkel, of zijn lengte, is evenredig met zijn straal. Dit betekent dat hoe groter de straal, hoe groter de contour de omtrek, volgens de vergelijking:

Kan u van dienst zijn: Correlatiecoëfficiënt: formules, berekening, interpretatie, voorbeeld

C = 2πr

Waar C de contour of lengte is, is R de radio en π (leest "pi") is een constante waarvan de geschatte waarde πAMP3 is.14 ..

4. Kosten voor het verzenden van een pakket

Omdat het gemakkelijk is om af te leiden, is de zwaardere of omvangrijke een duurdere pakket om het te vervoeren. Bedrijven die zich toeleggen op vrachttransportmodelleren hun prijzen volgens bepaalde regels, bijvoorbeeld:

C (x) = 2.75x

In deze vergelijking is C (x) de dollarkosten om een ​​pakket te verzenden waarvan het gewicht x pond is. De constante waarde 2.75 heeft eenheden van dollar/pond (eenheidskosten).

Situaties waarin kwadratische functies verschijnen

Algebraïsch wordt een kwadratische functie weergegeven door:

f (x) = a₂ X² + naar₁ x + a_of

Met de voorwaarde waarvoor de coëfficiënt is₂ Wees anders dan 0. Het wordt gekenmerkt door zijn parabola -vormige grafiek, waarvan de axiale as of symmetrieas verticaal is (parallel aan de y -as))).

De kruising tussen de gelijkenis en genoemde as is een punt genaamd Vertex. Als de gelijkenis opent (a₂ > 0), het hoekpunt is het minimumpunt en als het opent (a₂ < 0), es el máximo.

Op de as van symmetrie staat de focus, een speciaal punt dat de kromming van de parabool bepaalt. Als zonlicht wordt beïnvloed op een parabolische spiegel, worden de stralen weerspiegeld op het oppervlak, samenvallen in de focus, die onmiddellijk wordt verwarmd.

Modelleringsvoorbeelden met kwadratische functies

1. Hoogte van een projectiel gelanceerd verticaal omhoog

Een projectiel is elk object waaraan een initiële snelheid wordt verstrekt en vervolgens vrijgegeven, onder de actie van de zwaartekracht. Als de initiële snelheid verticaal is, is magnitude v₀ en opgericht, zal het object een maximale hoogte stijgen en vervolgens afdalen.

Kan u van dienst zijn: Homotecia

De hoogtevergelijking H als functie van tijd t is:

H (t) = −4.9 t²+v₀ T

Waar de verticale zin als positief wordt beschouwd, en het verticale down negatief.

2. Het traject van een horizontaal of schuin projectiel

Als een horizontale of schuine initiële snelheid wordt verstrekt aan een projectiel, zal deze een parabolisch traject beschrijven, dat kan worden weergegeven door een kwadratische functie zoals eerder beschreven.

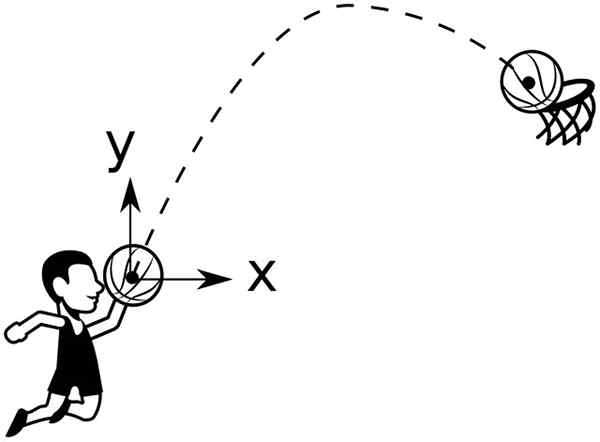Basket's bal beschrijft een parabolisch traject dat in de mand wordt gegooid. Bron: Wikimedia Commons

Bijvoorbeeld een bal gegooid van een hoogte en₀, Angle θ vormen₀ Wat de horizontale betreft, heeft het een traject gegeven door:

Met G als de versnelling van de zwaartekracht, die 10 m/s kan benaderen². Bijvoorbeeld, een voetbalkogels van de grond (en₀ = 0), met initiële snelheid van 6 m/s en hoek van 45º ten opzichte van de horizontale, zal een traject hebben gegeven door de volgende gelijkenis:

3. Het gebied van een cirkel

Hoe hoger de straal van de cirkel, hoe groter het gebied zal zijn. Inderdaad, het cirkelgebied is evenredig met het kwadraat van de straal R, de constante van evenredigheid is het getal π:

A = πr²

4. Effectiviteit van een advertentie

Hoe meer ze het zien, hoe effectiever een commerciële advertentie. Effectiviteit E, op een schaal van 0 tot 10, van één kennisgeving kan worden gemodelleerd volgens de volgende kwadratische functie:

Referenties 

1. Polynoomfuncties. Hersteld van middelen.onderwijs.is.
2. Larson, r. (2012). Voorzetting. 8e. editie. Cengage leren.
3. Miller, c. (2013). Wiskunde: redeneren en applicaties. 12e. editie. Pearson Education.
4. Stewart, J. (2012). Voorzetting. Wiskunde voor berekening. 6e. editie. Cengage leren.
5. Zill, D. (2008). Voorrang op berekening vooruitgang. 4e. editie. McGraw Hill.