Continuïteitsvergelijking

We leggen uit wat de continuïteitsvergelijking is, de formule, toepassingen, voorbeelden en stellen oefeningen voor om op te lossen

Wat is de continuïteitsvergelijking?

De continuïteitsvergelijking, Voor niet -samendrukbare vloeistof stelt het vast dat de totale massa van een vloeistof die door een buis circuleert, zonder verlies of winst, constant blijft. Met andere woorden, het deeg wordt behouden zonder veranderingen terwijl de vloeistof beweegt.

Een niet -samendrukbare vloeistof is dat wiens dichtheid ongeveer constant blijft tijdens het stromen. Water is bijvoorbeeld een vloeistof die wordt beschouwd als niet -samendrukbaar onder standaarddruk- en temperatuuromstandigheden.

Er is een wiskundige manier om het behoud van massa uit te drukken, in de continuïteitsvergelijking, gegeven door:

NAAR₁∙ V₁ = A₂∙ V₂

Waar v₁ en v₂ Ze vertegenwoordigen de snelheid van de vloeistof in twee secties van een pijp, terwijl₁ al₂ Het zijn de respectieve kruis -sectionele gebieden.

Het product van het kruis -sectionele gebied door snelheid wordt genoemd stroom En de continuïteitsvergelijking houdt in dat de stroom in de pijp constant is. De stroom staat ook bekend als Volumestroomsnelheid, Het wordt begrepen door de vorige uitdrukking zorgvuldig te observeren, waarvan de afmetingen volume per tijdseenheid zijn.

Formule

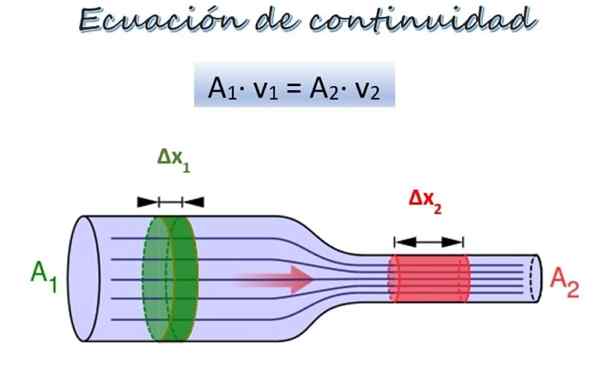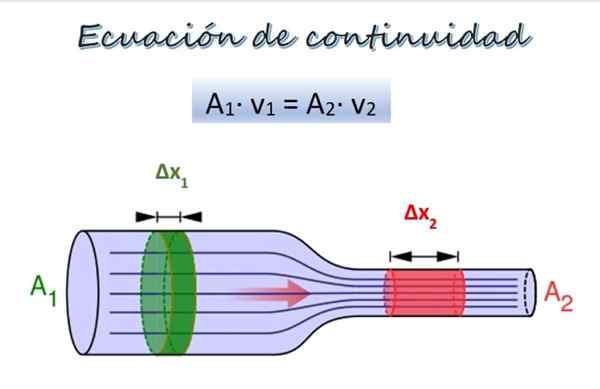
De continuïteitsvergelijking voor de stroom van een vloeistof langs een buis van verschillende diameters. Bron: Wikimedia Commons/F. Zapata.

In de bovenste afbeelding is er een pijp met twee delen van verschillende diameter en op dezelfde hoogte, hoewel ze op verschillende hoogten kunnen zijn zonder een probleem te vertegenwoordigen.

In sectie 1, breder, is het kruis -sectionele gebied om₁ en de vloeistof beweegt met snelheid V₁, Terwijl in sectie 2, smaller, het kruis -sectiegebied is om₂ en de snelheid van de vloeistof is V₂.

Een deeggedeelte Δm₁ (groen) beweegt op sectie 1 in een tijd Δt. Tijdens deze periode, het gedeelte Δm₂ (rood) Reis door sectie 2. Aangezien de vloeistof niet samendrukbaar is, is de dichtheid in al zijn punten hetzelfde, dus beginnend bij de definitie van dichtheid:

Het kan u van dienst zijn: GASE CONSTANT: Wat is berekening en voorbeelden

Hier is ρ dichtheid, m is de massa- en V -volume. Volgens dit, de massa AM₁ is gelijk aan:

AM₁ = ρ ∙ v₁

Waar volume v₁ Het is het product tussen de dwarsdoorsnede en de afstand Δx₁:

AM₁ = ρ ∙ (a₁ ∙ Δx₁))

Maar sinds:

Dan het deeggedeelte Δm₁ U kunt schrijven, in termen van snelheid en tijd Δt als:

AM₁ = ρ ∙ a₁ ∙ Δx₁ = ρ ∙ a₁ ∙ (v₁ ∙ Δt)

Analoog De portie Δm is geschreven₂ Dat stroomt tegelijkertijd in sectie 2:

AM₂ = ρ ∙ a₂ ∙ Δx₂ = ρ ∙ a₂ ∙ (v₂ ∙ Δt)

Door behoud van de massa:

AM₁ = AM₂

EN:

ρ ∙ a₁ ∙ V₁ ∙ Δt = ρ ∙ a₂ ∙ V₂ ∙ Δt

Aangezien Δt en ρ worden geannuleerd, resultaten:

NAAR₁ ∙ V₁ = A₂ ∙ V₂

De stroom q

Het product van de dwarsdoorsnede A door de snelheid van de vloeistof V wordt flow genoemd en wordt aangegeven als Q. Het is equivalent aan het volume vloeistof per tijdeenheid door de pijp, of volumestroomsnelheid:

 V Volume en Δt het tijdsinterval. De stroomsnelheid in het internationale systeem van eenheden is m³/s, hoewel kubieke voet, gallons/min, gallons/s a liters/s en gallons/s frequent zijn. Enkele van de meest gebruikte conversiefactoren zijn de volgende:

• 1 m³/S = 264.172 gal/s
• 1 l/s = 0.001 m³/S
• 1 ft³/S = 0.0283168 m³/S
• 1 l/s = 0,264172 gal/s
• 1 m³/S = 15850.3 gal/min

Merk op dat, door de dwarsdoorsnede van de buis te verlagen, de snelheid van de vloeistof toeneemt en vice versa, als de dwarsdoorsnede toeneemt, de snelheid afneemt zodat de stroom constant is.

Toepassingen en voorbeelden

De continuïteitsvergelijking wordt gebruikt bij de analyse van de vloeistofstroom, in combinatie met de Bernoulli -vergelijking, waarbij rekening wordt gehouden.

Kan u van dienst zijn: Directe stroom

voorbeeld 1

In de familietuinslang, wanneer het water normaal verlaat, heeft de straal een bepaald bereik, maar als het zijn vinger naar de uitgang van de slang legt, waardoor het uitgangsgat wordt verminderd, is het bereik van de straal groter groter.

Hier wordt de continuïteitsvergelijking vervuld, omdat, door, door het gebied van het uitgangsmondstuk te verlagen, de snelheid van de straal toeneemt zodat het snelheidsgebied door snelheid constant is.

Voorbeeld 2

De waterstraal smaller terwijl hij valt, omdat de snelheid toeneemt. Op deze manier blijft de productsnelheid per gebied constant

Een ander voorbeeld waarbij de continuïteitsvergelijking wordt benadrukt, is de waterstraal die smaller als deze valt, vanwege de toename van de watersnelheid tijdens de herfst.

Op deze manier is de stroom constant, terwijl de straal blijft stromen in een laminair regime, dat wil zeggen dat het water zachtjes valt zonder turbulentie of wervelingen.

Opgeloste oefeningen

Oefening 1

Water circuleert door een buis met een diameter van 20 cm. Wetende dat de stroom 2000 l/s is, zoek de watersnelheid in de pijp.

• Oplossing

Het is handig om alles uit te drukken in eenheden van het internationale systeem. Eerst wordt het kruis -sectionele gedeelte van de pijp berekend, die onthouden dat de straal de helft van de diameter is:

A = π ∙ (d/2)²

D = 20 cm = 0.2 m

Daarom is het gebied:

A = π ∙ (d/2)² = A = π ∙ (0.2 m /2)² = 0.0314 m².

De stroom wordt uitgedrukt in m³/s met behulp van de juiste conversiefactor:

Q = 2000 l/s = 2 m³/S

Uit de formule q = a ∙ v De snelheid waarmee de vloeistof door de pijp circuleert, wordt gewist:

Oefening 2

U hebt een variabele kruisingspijp waardoor water stroomt. Op een gegeven moment is de dwarsdoorsnede 0.070 m² En de snelheid van water is 3.50 m/s. Berekenen:

Kan u van dienst zijn: Pascal Principle: geschiedenis, toepassingen, voorbeelden

a) De watersnelheid op een ander punt in de pijp waarvan het dwarsdoorsnede -gebied 0 is.105 m².

b) Het volume water dat in 1 uur door een open uiteinde wordt gelost.

• Oplossing voor

De continuïteitsvergelijking wordt gebruikt, waarbij de stroom van het eerste punt overeenkomt met de stroom van de tweede. De stroom is:

Q = A ∙ V

Voor continuïteit:

Q₁ = Q₂

NAAR₁ ∙ V₁ = A₂ ∙ V₂

Nu vervangen ze de gegevens van de verklaring:

• NAAR₁ = 0.070 m²
• v₁ = 3.50 m/s
• NAAR₂ = 0.105 m²
• v₂ =?

En wist V₂:

Oplossing B

Omdat de stroom ook het volume per tijdseenheid is, moet het:

Daarom is deel V:

V = q ∙ Δt = (a ∙ v) Δt

De stroom die kan worden berekend met de gegevens van punt 1 of die van punt 2, omdat deze op beide punten hetzelfde is:

Q = a₁ ∙ V₁ = 0.070 m² ∙ 3.50 m/s = 0.245 m³ / S

Wetende dat 1 uur = 3600 s, is het ontladen van water:

V = q ∙ Δt = (0.245 m³ / s) × (3600 s) = 882 m³

In 1 uur worden 882 m gedownload³ water door de pijp.