Synthetische verdeling

We leggen uit wat synthetische verdeling is, een methode om dit te doen, voorbeelden en oefeningen opgelost.

Wat is synthetische verdeling?

De Synthetische verdeling Het is een eenvoudige manier om een ​​polynoom p (x) te verdelen door een van de vorm d (x) = x - c - c. Bijvoorbeeld polynoom p (x) = (x⁵+3x⁴-7x³+2x²-8x+1) Het kan worden weergegeven als de vermenigvuldiging van de twee eenvoudigste polynomen (x+1) en (x⁴ + 2x³)).

Het is een zeer nuttig hulpmiddel, omdat het, naast ons in staat te stellen polynomen te verdelen, het ook mogelijk maakt om een ​​P (x) polynoom in een getal C te evalueren, wat ons op zijn beurt precies aangeeft als dat nummer een nul is of niet van de polynoom.

Dankzij het divisie -algoritme weten we dat als we twee p (x) en d (x) polynoom (x) + r (x) hebben, waarbij r (x) nul is of minder is dan q (x). Deze polynomen staan ​​respectievelijk bekend als quotiënt en residu of rust, respectievelijk.

Bij de gelegenheden waarin polynoom D (x) van de X - C -vorm is, geeft de synthetische verdeling ons een korte manier om te vinden wie Q (x) en R (x) zijn.

Synthetische divisiemethode

Laat p (x) = a_NX^N+naar_N-1X^N-1+… +A₁x+a₀ De polynoom die we willen delen en d (x) = x-c de deler. Om te delen door de synthetische divisiemethode gaan we als volgt verder:

1- We schrijven de coëfficiënten van P (x) op de eerste rij. Als er geen X -kracht verschijnt, plaatsen we nul als zijn coëfficiënt.

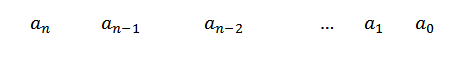
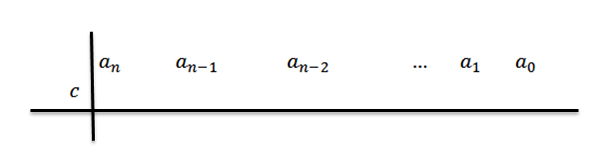
2- In de tweede rij, links van een_N We plaatsen C en trekken divisielijnen, zoals getoond in de volgende figuur:

3- We verlagen de toonaangevende coëfficiënt naar de derde rij.

Kan u van dienst zijn: Euler -methode: wat is het gebruik van procedure en oefeningen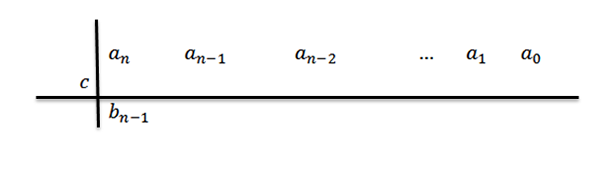

In deze uitdrukking B_N-1= A_N

4- We vermenigvuldigen C door de toonaangevende coëfficiënt B_N-1 En we schrijven het resultaat in de tweede rij, maar een kolom rechts.

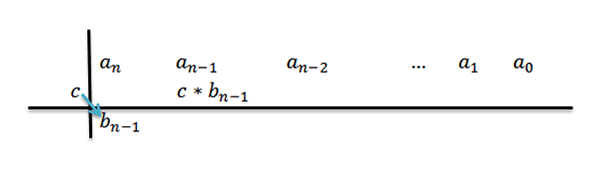
5- We voegen de kolom toe waar we het vorige resultaat schrijven en het resultaat wordt onder genoemde som geplaatst. Dat is in dezelfde kolom, derde rij.

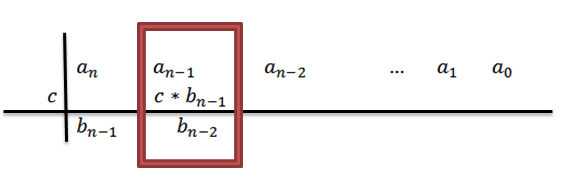
Door toe te voegen, hebben we daardoor_N-1+C*B_N-1, waarvoor we voor comfort zullen bellen_N-2

6- We vermenigvuldigen c met het vorige resultaat en schrijven het resultaat rechts op de tweede rij.

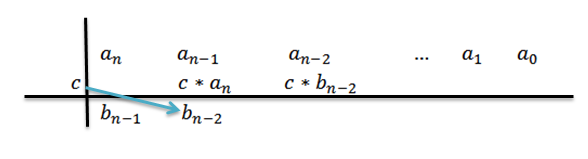
7- We herhalen stap 5 en 6 totdat we de coëfficiënt bereiken₀.

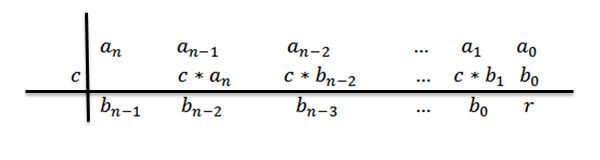
8- We schrijven het antwoord, dat wil zeggen het quotiënt en het residu. Terwijl we de divisie doen van een cijfer N polynoom tussen een polynoom van graad 1, hebben we dat het quotiënt graad N-1 zou zijn.

De coëfficiënten van het quotiëntpolynoom zullen het aantal van de derde rij zijn, behalve de laatste, die het residupolynoom of de rest van de divisie zal zijn.

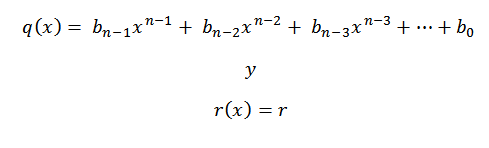
Opgeloste oefeningen

voorbeeld 1

Maak de volgende deling volgens de synthetische divisiemethode:

(X⁵+3x⁴-7x³+2x²-8x+1): (x+1).

Oplossing

Eerst schrijven we de dividendcoëfficiënten als volgt:

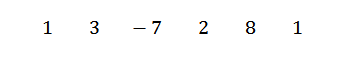
Dan schrijven we C aan de linkerkant, op de tweede rij, samen met de divisielijnen. In dit voorbeeld C = -1.

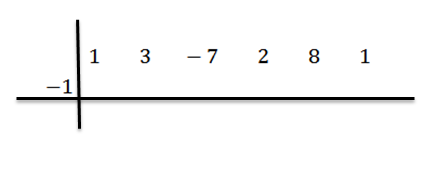
We verlagen de leidende coëfficiënt (in dit geval B_N-1 = 1) en we vermenigvuldigen het met -1:

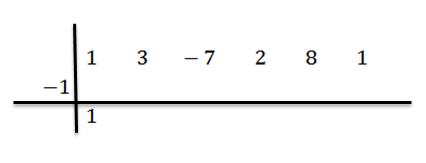
We hebben het resultaat rechts op de tweede rij geschreven, zoals hieronder getoond:

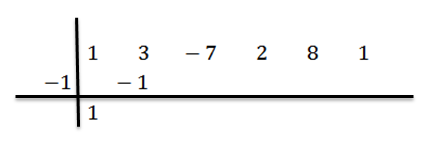
We voegen de nummers van de tweede kolom toe:

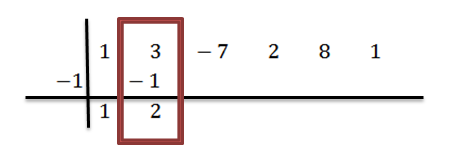
We vermenigvuldigen 2 met -1 en schrijven het resultaat in de derde kolom, tweede rij:

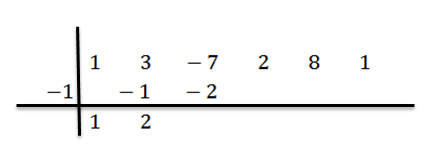
We voegen de derde kolom toe:

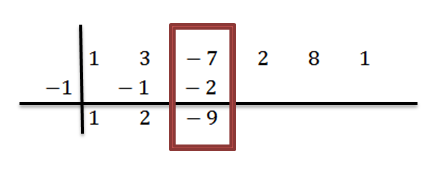
We gaan analoog tot we de laatste kolom bereiken:

Kan u van dienst zijn: standaard en overtollige aanpak: wat is en voorbeelden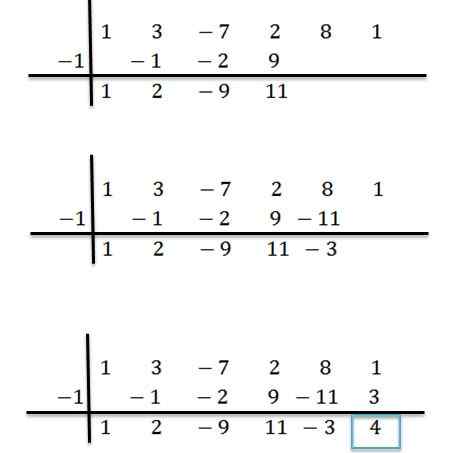

We hebben dus dat het laatste verkregen nummer de rest van de divisie is, en de resterende getallen zijn de coëfficiënten van het quotiëntpolynoom. Dit is als volgt geschreven:

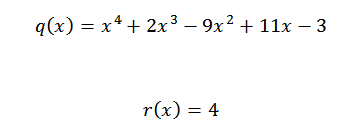
Als we willen verifiëren dat het resultaat correct is, is het voldoende om te verifiëren dat aan de volgende vergelijking wordt voldaan:

P (x) = q (x)*d (x) + r (x)

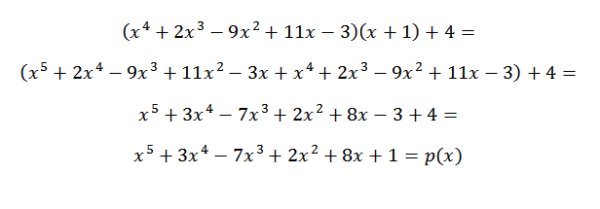
We kunnen dus verifiëren dat het verkregen resultaat correct is.

Voorbeeld 2

Voer de volgende polynoomverdeling uit volgens de synthetische divisiemethode:

(7x³-x+2): (x+2)

Oplossing

In dit geval hebben we dat de term x² Het verschijnt niet, dus we zullen naar 0 schrijven als zijn coëfficiënt. Aldus zou de polynoom blijven als 7x³+0x²-x+2.

We schrijven uw coëfficiënten op een rij, dat is:

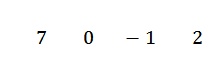
We schrijven de waarde van C = -2 aan de linkerkant in de tweede rij en trekken de divisielijnen.

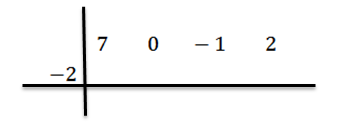
We verlagen de toonaangevende coëfficiënt B_N-1 = 7 en we vermenigvuldigen het met -2, schrijven het resultaat in de tweede rij naar rechts.

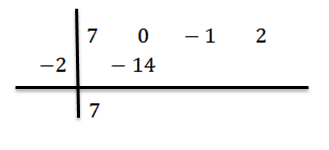
We voegen en gaan door, zoals eerder uitgelegd, totdat we de laatste termijn bereiken:

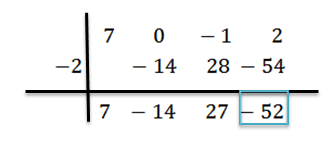
In dit geval is de rest r (x) = -52 en is het verkregen quotiënt q (x) = 7x²-14x+27.

Voorbeeld 3

Een andere manier om synthetische verdeling te gebruiken is als volgt.

Voor het divisie -algoritme kunnen we de P (x) polynoom als volgt schrijven:

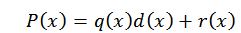
In deze uitdrukking zijn q (x) en r (x) respectievelijk het quotiënt en de rest. Nu, als d (x) = x-c, bij het evalueren in c in polynoom, vinden we het volgende:

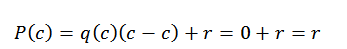
Dit is de reden waarom het alleen maar overblijft om R (X) te vinden, en we kunnen dit doen dankzij de synthetische verdeling.

We hebben bijvoorbeeld polynoom p (x) = x⁷-9x⁶+19x⁵+12x⁴-3x³+19x²-37x-37 en we willen weten wat de waarde ervan is bij het evalueren op x = 5. Hiervoor voeren we de verdeling uit tussen p (x) en d (x) = x -5 volgens de synthetische divisiemethode:

Kan u van dienst zijn: axiale symmetrie: eigenschappen, voorbeelden en oefeningen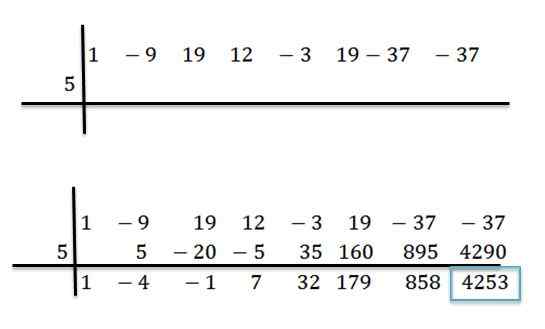

Zodra de bewerkingen zijn uitgevoerd, weten we dat we P (x) als volgt kunnen schrijven:

P (x) = (x⁶-4x⁵ -X⁴+ 7x³ +32x² +179x + 858)*(x-5) + 4253

Daarom moeten we bij het evalueren:

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(5-5) +4253

P (5) = (5-4 (5) -5 +7 (5) +32 (5) +179 (5) +858)*(0) +4253

P (5) = 0 + 4253 = 4253

Zoals we kunnen zien, is het mogelijk om de synthetische verdeling te gebruiken om de waarde van een polynoom te vinden bij het evalueren in C in plaats van het eenvoudig vervangen van C door X. 

Als we P (5) op de traditionele manier proberen te evalueren, hebben we enkele berekeningen nodig die meestal vervelend worden.

Voorbeeld 4

Het divisie -algoritme voor polynomen wordt ook voldaan voor polynomen met complexe coëfficiënten en bijgevolg hebben we dat de synthetische divisiemethode ook voor deze polynomen werkt. Vervolgens zullen we een voorbeeld zien.

We zullen de synthetische divisiemethode gebruiken om aan te tonen dat z = 1+ 2i een nul is van de polynoom p (x) = x³+ (1+i) x² -(1+2i) x+(15+5i). Dat wil zeggen, het residu van de divisie P (x) tussen d (x) = x - z is gelijk aan nul.

We gaan door zoals voorheen: in de eerste rij schrijven we de coëfficiënten van P (x), dan schrijven we in het tweede zend en tekenen we de divisielijnen.

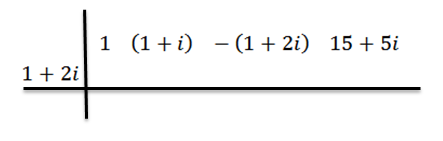
We doen de divisie zoals voorheen, dat is:

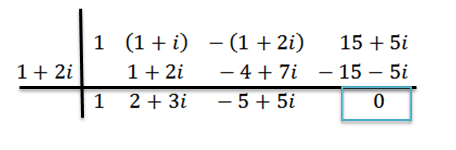
We kunnen zien dat het residu nul is; Daarom concluderen we dat z = 1+ 2i een nul van P (x) is.

Referenties

1. Baldor, Aurelio. Algebra. Patria -redactiegroep.
2. Demana, Waits, Foley & Kennedy. Precáculo: grafisch, numeriek, algebraïsch. Pearson Education.