Discrete distributies
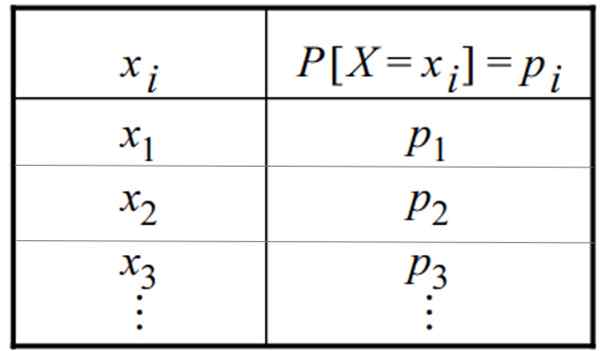
- 3691
- 541
- Miss Herman Russel
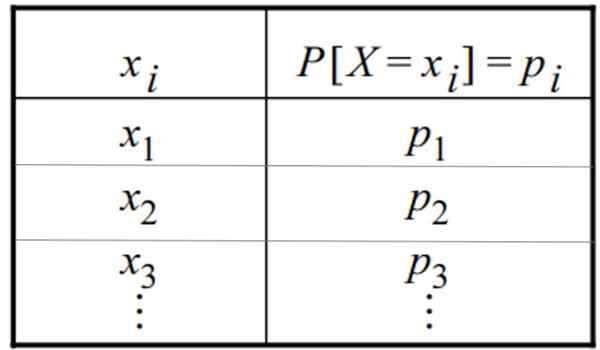 Tabel met een discrete waarschijnlijkheidsverdeling. Bron: f. Zapata
Tabel met een discrete waarschijnlijkheidsverdeling. Bron: f. Zapata Wat is een discrete verdeling?
A discrete verdeling van waarschijnlijkheden is een functie f (xJe) die toewijst aan elke waarde van een discrete variabele: x1, X2, X3,... XJe, Een zeker voorkomen van voorkomen P (x = xJe)). Deze functie staat ook bekend als "waarschijnlijkheidsmassfunctie".
De discrete waarschijnlijkheidsverdeling kan worden gegeven in de vorm van een tabel of afbeeldingen. Een tabel heeft deze algemene vorm, waarin de variabele in de ene kolom verschijnt en de respectieve waarschijnlijkheid ervan in de andere:
Waarschijnlijkheidsmassafuncties delen de volgende algemene kenmerken:
- De waarschijnlijkheid pJe van elk X -evenementJe Het is tussen 0 en 1, zelfs sommige van deze limietwaarden zijn: 0 ≤ x ≤ 1.
- P (x = xJe) = PJe Neem daarom positieve waarden, dus: P (x = xJe) ≥ 0.
- Het is waar dat ∑ p (xJe) = 1 voor alle mogelijke waarden van x.
Een waarschijnlijkheidsverdeling beschrijft het gedrag van een populatie, beschreven door zijn parameters: de gemiddelde μ, de variantie σ2 en de standaardafwijking S = σ σ2.
Vervolgens worden de meest opvallende discrete distributies kort beschreven:
Uniforme verdeling
Het is de eenvoudigste discrete verdeling van allemaal. Daarin kan de variabele "n" discrete waarden nemen: x1, X2, X3,... XJe, Allemaal met dezelfde probabblaity. In dit geval wordt de verdeling gegeven door:
Binomiale verdeling
Het is van toepassing op ervaringen met slechts twee mogelijke en wederzijds exclusieve resultaten, die meestal "succes" en "falen" worden genoemd, aangeduid als respectievelijk E en F. Het feit dat een gebeurtenis 'succes' wordt genoemd, betekent niet noodzakelijkerwijs dat het een goede zaak is, het is eerder een willekeurige aanduiding.
De kans op succes p (e) in "n" repetities, wordt aangeduid als p, en die van falen p (f) zoals q = 1 - p.
Als "X" een bepaald aantal successen vertegenwoordigt in de "N" onafhankelijke proeven, is het waar dat: 0 ≤ x ≤ n. En de kans op voorkomen P (x) van de gebeurtenis wordt berekend door de volgende formule:
Het kan u van dienst zijn: vierkante centimeters tot vierkante meter (cm² tot m²)Waar x = 0, 1, 2, 3 ..., n en het symbool (!) betekent "faculteit":
X! = x ∙ (x - 1) ∙ (x - 2) ∙ (x - 3)… 1
0! = 1
Poisson -verdeling
In deze verdeling geeft de willekeurige variabele x aan hoe vaak een gebeurtenis in een bepaalde interval plaatsvindt, wat tijd, afstand of andere kan zijn. De gebeurtenissen van de gebeurtenis zijn willekeurig, onafhankelijk en worden gelijkmatig verdeeld gedurende het interval in kwestie.
Zodra deze voorwaarden, worden de waarschijnlijkheid, die afhankelijk is van het gemiddelde van μ -voorvallen en het aantal Euler of nummer "E", berekend door:
De kansen op gebeurtenissen met deze verdeling zijn klein, dus het wordt de "wet van zeldzame zaken" genoemd.
Binomiale distributiebenadering
De verdeling van Poisson dient als een benadering van binomiale verdeling wanneer N groot is (n≥ 100) en P klein is (NP ≤ 10). In dit geval wordt de gemiddelde μ berekend als:
μ = n ∙ p
Hypergeometrische verdeling
Het wordt gebruikt wanneer de kansen niet onafhankelijk zijn, dat wil zeggen, na het uitvoeren van het experiment, zijn de omstandigheden niet weer hetzelfde. Dit is wat er gebeurt bij het extraheren van monsters zonder vervanging van een populatie, dus de binomiale verdeling kan niet meer worden gebruikt.
Als de populatie bestaat uit twee soorten objecten die verschillen van en B, en bij willekeurige objecten en zonder vervanging, is de kans op het verkrijgen van X -objecten van type A:
Waarbij a en b de respectieve hoeveelheden objecten van elk type zijn, aanwezig in de populatie.
Als de populatie echter erg groot is, zelfs als er geen vervanging is, is het moeilijk voor hetzelfde element dat meer dan eens wordt geselecteerd, dus beide distributies: binomiaal en hypergeometrisch, produceren vergelijkbare resultaten.
Kan u van dienst zijn: Cubes Differention: Formules, Vergelijkingen, Voorbeelden, oefeningenVoorbeelden
Munten worden gelanceerd
Co -launches zijn zeer illustratieve voorbeelden:
-De lancering van een eerlijke valuta, en krijg een gezicht. Het is bekend dat 1 gezicht ½ kans heeft om te vertrekken en het kruis (0 gezicht), hetzelfde. De verdeling wordt in deze tabel weergegeven:
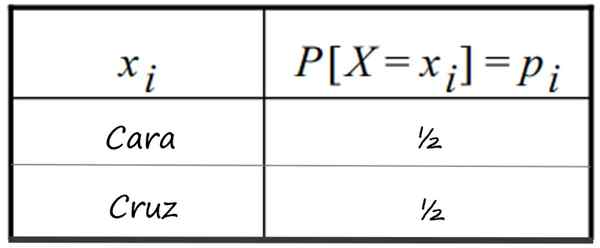 Discrete waarschijnlijkheidsdistributietabel die volgt op de lancering van 1 eerlijke valuta. Bron: f. Zapata
Discrete waarschijnlijkheidsdistributietabel die volgt op de lancering van 1 eerlijke valuta. Bron: f. Zapata -Het gelijktijdige schot van twee Eerlijke munten en mogelijke gezichten nummers die kunnen worden verkregen.
 Discrete waarschijnlijkheidsdistributietabel die volgt op de lancering van twee eerlijke valuta, met het oog op het verkrijgen van een gezicht of niet. Bron: f. Zapata
Discrete waarschijnlijkheidsdistributietabel die volgt op de lancering van twee eerlijke valuta, met het oog op het verkrijgen van een gezicht of niet. Bron: f. Zapata Variabelen met een uniforme verdeling
-De selectie van een geheel getal dat even of oneven is: elk is waarschijnlijkheid gelijk aan ½ van de gekozen binnen de set van hele getallen.
-De lancering van een eerlijke dobbelstenen. In dit geval zijn er 6 genummerde gezichten en elk heeft dezelfde kans om te vertrekken: 1/6.
-De selectie van een onderwerp om een examen af te leggen, gekozen uit tussen n problemen, als ze allemaal even waarschijnlijk zijn.
Variabelen met binomiale verdeling
-Aantal gezichten dat uitkomt door een eerlijke munt te lanceren.
-Van een bevolking van 250 gezinnen, het aantal van deze dat 2 kinderen heeft.
-De hoeveelheid rozenhout die overleeft, na een tuinman 20 Rosales in een tuin.
-Van een studie met 50 patiënten, het aantal van hen dat een negatieve reactie op een medicijn presenteerde.
-Het aantal studenten goedgekeurd in een waarschijnlijkheidsexamen, van een groep die bestaat uit 100 studenten.
Variabelen met Poisson -verdeling
-Aantal oproepen per minuut tot Callcenter Van een bedrijf.
-Aantal grote aardbevingen per jaar voor een specifiek geografisch gebied.
-Het aantal tornado's dat het afgelopen jaar een bepaalde regio heeft beïnvloed.
-Aantal bomen geïnfecteerd met een schimmel, per vierkante hectare bos.
Variabelen met hypergeometrische verdeling
-Successen van cijfers of winnende combinaties in gokken.
Kan u van dienst zijn: Gelijktijdige vectoren: kenmerken, voorbeelden en oefeningen-Selectie van een bepaald aantal vrouwen of mannen in een monster van N -vissen van een vissenkom.
Opgeloste oefeningen
Oefening 1
Een studie bepaalde dat door willekeurig geselecteerde volwassenen die smartphones hebben, 54% van hen ze gebruikt in de klas of vergaderingen. U wilt de kans vinden dat, willekeurig 8 mensen met smartphone selecteren, precies 6 van hen in de klas of vergaderingen gebruiken.
Oplossing
Dit experiment komt overeen met een binomiaal experiment, omdat het resultaat binair is: een persoon neemt de telefoon in de klas of haalt het niet uit. Het feit dat de persoon de telefoon in de klas gebruikt, kan succes worden genoemd, en een mislukking als dit niet het geval is (voordat deze werd uitgelegd dat deze keuze volledig willekeurig is).
In dat geval: p = 0.54 en Q = 1- 0.54 = 0.46.
Aangezien 8 mensen willekeurig worden geselecteerd, dan n = 8 en de waarde van x is 6, daarom zijn de nodige waarden beschikbaar om ze te vervangen in de binomiale distributieformule:
Oefening 2
Voor een recent jaar registreerde een kliniek 4221 geboorten. Bepaal met deze unieke gegevens de kans dat er 15 geboorten zijn in 1 dag. Is deze gebeurtenis zeldzaam?
Oplossing
Poisson -verdeling wordt gebruikt, zoals wordt gevraagd om de waarschijnlijkheid van het optreden van een gebeurtenis te bepalen die in een tijdsinterval optreedt. In dit geval is de variabele de hoeveelheid geboorten en het interval is 1 dag.
De Poisson -distributieformule heeft de gemiddelde geboorte per dag nodig, die gemakkelijk wordt berekend:
Daarom is de kans op x = 15 geboorten/dag:
Het resultaat kan worden uitgedrukt in termen van percentage voor duidelijkheid: 6.42% waarschijnlijk dat op elke dag precies 15 geboorten optreden. Het evenement is onwaarschijnlijk, hoewel in geen enkel geval onmogelijk.


=\frac1n)
=\fracn!\left&space;(&space;n-x&space;\right&space;)!\cdot&space;x!\cdot\:p^x\cdot&space;q^n-x)
=\frac\mu&space;^x\cdot&space;e^-\mu&space;x!)
=\fracA!\left&space;(A-x&space;\right&space;)!\cdot&space;x!\cdot&space;\fracB!\left&space;(B-n+x&space;\right&space;)!\cdot&space;\left&space;(n-x&space;\right&space;)!\div&space;\frac\left&space;(A+B&space;\right&space;)!\left&space;(A+B-n&space;\right&space;)!\cdot&space;n!)
=\frac8!\left&space;(8-6&space;\right&space;)!\times&space;6!\times&space;0.54^6\times&space;0.46^\left&space;(8-6&space;\right&space;)=\frac8!2!\times&space;6!\times&space;0.54^6\times&space;0.46^2=0.147)

=\frac11.56^15\times&space;e^-11.5615!=0.0642)