Algemene cultuur en samenleving

Exponentiële verdeling

1957
350
Glen Armstrong

We leggen uit wat exponentiële verdeling is, de kenmerken, formules, voorbeelden en opgeloste oefeningen

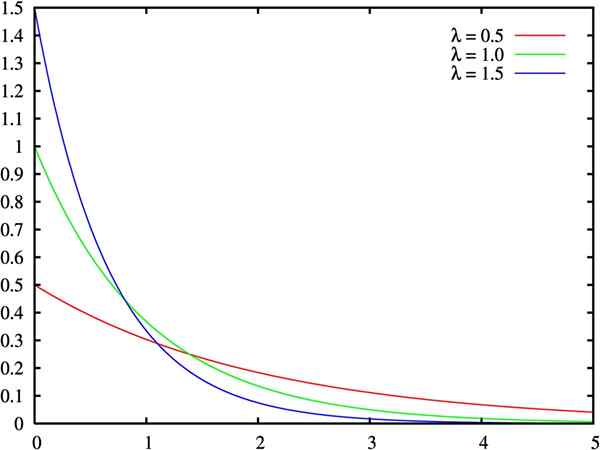
Grafiek van de dichtheidsfunctie van de exponentiële verdeling, voor drie waarden van de lambda -parameter. Bron: Wikimedia Commons.

Wat is exponentiële verdeling?

De exponentiële verdeling Het is een probabilistisch model voor continue willekeurige variabelen. Dit betekent dat u hierdoor de kans kunt weten van het optreden van een bepaalde waarde van de variabele, dus het is een waarschijnlijkheidsverdeling.

Om de distributie te verkrijgen, begint deze vanaf een Dichtheidsfunctie, die een exponentiële vorm heeft van parameter λ> 0:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ tekst Ja x \ leq 0 \ End cases$

De dichtheidsfunctie als zodanig maakt het niet mogelijk om de waarschijnlijkheid te berekenen, maar eenmaal vastgesteld f (x), wordt de distributiefunctie f (x), waarmee de kansen worden verkregen, verkregen door integratie van f (x). De waarschijnlijkheid P dat de willekeurige variabele bijvoorbeeld waarden tussen 0 en x neemt, is:

$F(x)=P[x\leq x]=\int_0^xf(x)dx$

Het uitvoeren van de integratie, die heel eenvoudig is, omdat de integrale van een exponentiaal hetzelfde exponentieel is, behalve de constanten die het argument vergezellen, wordt het verkregen:

$F(x)=\int_0^x\lambda e^-\lambda xdx=\lambda \left (-\frac1\lambda \right )\left [ e^-\lambda x \right ]_0^x=-\left (e^-\lambda x-e^0 \right )=1-e^-\lambda x$

De exponentiële verdeling wordt veel gebruikt om de waarschijnlijkheid van een gebeurtenis na een bepaalde wachttijd te bepalen, zoals de tijd die plaatsvindt in de opkomst van een ziekenhuis voordat een patiënt arriveert.

Vaak verwijzen gebeurtenissen naar het falen of de afbraak van elektrische, elektronische en andere typen. In dit geval helpt de exponentiële verdeling de tijd om de tijd te schatten voordat een component faalt, en ook de tijd tussen reparaties. Dit staat bekend als betrouwbaarheidstheorie.

Kenmerken van exponentiële verdeling

Enkele van de meest opvallende kenmerken van de dichtheidsfunctie F (x) van de exponentiële verdeling zijn de volgende:

F (x) is positief.
Het gebied onder de curve y = f (x) = λe^−λ^X Het is altijd gelijk aan 1, omdat de som van de kansen van het optreden van alle waarden van de variabele moet zijn 1. Dit is een aandoening die dichtheidsfuncties vervullen. Dit gebied wordt berekend door de integraal:

Kan u van dienst zijn: Anuma

$\int_-\infty ^\infty f(x)dx=\int_-\infty ^\infty \lambda e^-\lambda xdx=1$

Gebrek aan exponentieel distributiegeheugen

Het meest opvallende kenmerk van exponentiële verdeling is het gebrek aan geheugen. Stel bijvoorbeeld dat de tijd die verstreken is, modelleert met deze verdeling totdat het falen van een element plaatsvindt.

Welnu, het gebrek aan geheugen verwijst naar weten dat het element voor een overlevingstijd van de "S" werkte, wijzigt niet de kans dat het element tot een bepaalde extra hoeveelheid tijd "T" zal blijven lopen.

Dat wil zeggen, de kans dat het element van hier tot een bepaalde tijd faalt (bijvoorbeeld 1 minuut, 1 uur), hangt niet af van het tot nu toe hebben gewerkt.

Wiskundig wordt het berekend per definitie van waarschijnlijkheid van onafhankelijke gebeurtenissen:

$P[x\geq s+t/x\geq s]=\fracP[x\geq s+t]P[x\geq s]=\frac1-F(s+t)1-F(s)=\frac1- [1-e^-\lambda (s+t) ]1- [1-e^-\lambda s ]= \beginmatrix \\ \endmatrix$

$=e^-\lambda t$

Daarom hangt de waarschijnlijkheid niet af van S of overlevingstijd.

Formules

1.- De dichtheidsfunctie van de exponentiële verdeling is:

$f(x)=\begincases \lambda e^-\lambda x& \text si x>0 \\ 0 & \ tekst Ja x \ leq 0 \ End cases$

Waarbij λ de distributieparameter is.

2.- Zoals hierboven beschreven, wordt de verdeling van kansen zelf aangeduid als F (x) en worden de verschillende kansen verkregen door integratie van de dichtheidsfunctie:

$F(x)=\begincases 0 & \text si x\leq 0 \\ 1-e^-\lambda x& \text si x>0 \ End cases$

3.- Uit het bovenstaande volgt dat de waarschijnlijkheid dat de variabele waarden kleiner dan of gelijk is aan "x" p [x≤x] = 1 −e is^−λ^X.

4.- Het gebied onder de curve y = f (x), opgenomen tussen a en b, maakt het mogelijk om de kans te berekenen dat de variabele zich in het interval bevindt [a, b]. Dit gebied is:

P [a ≤ x ≤ b] = f (b) - f (a)

5.- De waarde van p [x ≥ a] is 1 - f (a) = 1 - (1 - e^−λ^X) = e^−λ^X

Verwachte waarde van exponentiële verdeling

De hoop of verwachte waarde E (x) van de exponentiële verdeling is de waarde die naar verwachting vaker zal plaatsvinden. Het wordt berekend uit de integraal:

Kan u van dienst zijn: informatie -registratietechnieken

$E(x)=\int_0^\infty xf(x)dx$ Die gemakkelijk kan worden opgelost door de integratiemethode door onderdelen. Het resultaat is:

E (x) = 1/λ

Variantie van exponentiële verdeling

Voor de berekening van de variantie moet de integraal worden bepaald:

$Var(x)=\int_0^\infty x^2f(x)dx$

Die ook wordt opgelost met de integratiemethode door onderdelen, om te verkrijgen:

Var (x) = 1/λ²

Een bijzonderheid van exponentiële verdeling is dat de standaardafwijking s (x), gedefinieerd als de vierkantswortel van de variantie is:

S (x) = √var (x) = √ (1/λ²) = 1/λ

Dat wil zeggen, de standaardafwijking is gelijk aan de hoop op distributie.

Voorbeelden van exponentiële verdeling

Datatie van koolstofmonsters 14

De exponentiële verdeling wordt gebruikt om de tijd te bepalen die nodig is om een radioactief deeltje uiteen te vallen. Deze tijden worden tot op heden gebruikt fossiele monsters door radiokoolstof.

Tijd die nodig is om de e -mail te controleren

U kunt de tijd modelleren die gebruikers nemen om hun e -mail te bekijken, zodra de melding is ontvangen, via een exponentiële verdeling. Stel dat de distributieparameter λ = 0 is.2 dan is de kans dat een persoon minder dan 1 minuut nodig heeft om zijn e -mail te beoordelen:

$P[x\leq 1]=\int_0^1f(x)dx=\int_0^10.2e^-0.2xdx$

Deze integraal werd in het begin opgelost, het blijft alleen om de numerieke waarden in de oplossing te vervangen en het eindresultaat te berekenen:

P [x ≤ 1] = 1 --e^-^0.2^×¹ = 1− e^-^0.2 = 1− 0.819 = 0.181

Het kan ook direct worden vervangen op de hierboven gegeven F (x) -functie om F (1) te verkrijgen.

Opdrachten

Oefening 1

Zoek de kans dat een persoon later één uur zijn e -mail bekijkt, als de waarschijnlijkheidsverdeling exponentieel is, met parameter λ = 0.2.

Oplossing

P [x ≥ 60] moet worden berekend, aangezien 1 uur gelijk is aan 60 minuten en de kans dat de persoon eind 60 minuten of langer is gevraagd om te controleren. De waarschijnlijkheid wordt berekend met dezelfde integrale in het begin gepresenteerd, gewoon de integratielimieten wijzigen:

Can Serve You: Rapa Nui: Geschiedenis, kenmerken, cultuur, tradities

$P[x\geq 60]=\int_60^\infty 0.2e^-0.2xdx=-\left ( -e^-0.2\times 60 \right )=0.000006144$

De verkregen waarde is klein, dus het is zeer onwaarschijnlijk dat een persoon meer dan een uur nodig heeft om zijn e -mail te bekijken.

Oefening 2

De elektrische bollen hebben meestal een eindige duur, behalve de beroemde lamp van de brandweerkazerne in Livermore, Californië, die nooit heeft gefaald sinds het voor het eerst was, in 1901.

Neem aan dat de duur van een huidige lamp een exponentiële verdeling volgt, met een verwachte waarde van 8 maanden. Berekenen:

a) Wat is de kans dat de lamp tussen de 5 en 14 maanden zal duren?

b) De kans dat de lamp meer dan 25 maanden zal duren, wetende dat deze meer dan 11 maanden in bedrijf heeft.

Oplossing voor

Het eerste is om de waarde van λ te vinden, door de verwachte waarde van de verdeling E (x) = 8 maanden. Volgens wat er in de voorgaande sectie werd gezegd, is de verwachte waarde het omgekeerde van de λ -parameter, daarom:

E (x) = 1 /λ → λ = 1 /e (x) = 1/8 = 0.125

Vervolgens wordt de gevraagde waarschijnlijkheid berekend, door middel van de integrale die in het begin wordt gegeven, maar handig de integratielimieten wijzigen:

Vervolgens wordt het vervangen in de f (x) -functie in de voorgaande sectie, als volgt:

P [5 ≤ x ≤ 14] = f (14) - f (5) = [1 - e^{-(0.125 × 14)}] - [1 - E^{-(0.125 × 5)}] = 0.36

Oplossing B

Om dit probleem te beantwoorden, zal de eigenschap van het gebrek aan geheugen worden gebruikt, hierboven uitgewerkt. Omdat het bekend is dat het al meer dan 11 maanden heeft geduurd: dan:

S = 11 maanden

De extra tijd om 25 maanden of langer mee te gaan is:

T = 14 maanden

P [x ≥ s + t│t ≥ s] = p [x ≥ 11 + 14│t ≥ 11] = e^{−0.125 × 14}= 0.174