Euclidian afstandsconcept, formule, berekening, voorbeeld

De Euclidiaanse afstand Het is een positief getal dat de scheiding aangeeft die twee punten hebben in een ruimte waar aan de axioma's en stellingen van Euclid -geometrie worden voldaan.

De afstand tussen twee punten A en B van een Euclidische ruimte is de lengte van de vector Aab Behorend tot de enige lijn die door deze punten gaat.

Figuur 1 . Unidimensionale Euclidische ruimte gevormd door de lijn (ox). Verschillende punten op deze ruimte, hun coördinaten en afstanden worden getoond. (Opgesteld door Ricardo Pérez).

De ruimte die we waarnemen en waar we mensen verplaatsen, is een driedimensionale ruimte (3D), waarbij de axioma's en stellingen van euclide-geometrie worden vervuld. In deze ruimte zijn twee -dimensionale subruimten (plannen) en één -dimensionale (rechte) (rechte) subruimten.

Euclidische ruimtes kunnen van één dimensie (1-D), tweedimensies (2-D), drie dimensies (3-D) of N-dimensies (N-D) zijn.

Dit zijn punten in de ene -dimensionale ruimte x die behoren tot de georiënteerde lijn (ox), de richting van of naar X is het positieve adres. Om de punten op deze lijn te vinden, wordt het Cartesiaanse systeem dat bestaat uit het toewijzen van elk punt van de lijn een nummer gebruikt.

[TOC]

Formule

De Euclidiaanse afstand d (a, b) wordt gedefinieerd tussen punten A en B, gelegen op een lijn, zoals de vierkantswortel van het kwadraat van de verschillen van zijn X -coördinaten:

D (a, b) = √ ((xb - xa)^2)

Deze definitie garandeert dat: de afstand tussen twee punten is altijd een positief bedrag. En dat de afstand tussen A en B gelijk is aan de afstand tussen B en A.

Figuur 1 toont de ene -dimensionale Euclidian -ruimte gevormd door de lijn (ox) en verschillende punten op die lijn. Elk punt heeft een coördinaat:

Punt A heeft XA -coördinaat = 2.5, de B -coördinaat xb = 4 en het punt c coördinaat xc = -2.5

Het kan u van dienst zijn: frequentiekans: concept, hoe het wordt berekend en voorbeelden

D (a, b) = √ ((4 - 2.5) 2) = 1.5

D (b, a) = √ ((2.5 - 4) 2) = 1.5

D (a, c) = √ ((-2.5 - 2.5) 2) = 5.0

Euclidian afstand in twee dimensies

De twee -dimensionale euclide -ruimte is een vlak. De punten van een Euclidisch vlak ontmoeten bijvoorbeeld de axioma's van Euclid -geometrie, bijvoorbeeld:

- Op twee punten past een enkele lijn. 

- Drie punten op het vlak vormen een driehoek waarvan de interne hoeken altijd 180º toevoegen.

- In een rechthoekige driehoek is het vierkant van de hypotenuse gelijk aan de som van de vierkanten van zijn benen.

In twee dimensies heeft een punt X- en Y -coördinaten. 

Een punt P heeft bijvoorbeeld coördinaten (XP, YP) ​​en een punt dat gecoördineerd is (XQ, YQ).

Euclidische afstand tussen punt P en Q wordt gedefinieerd met de volgende formule:

D (p, q) = √ ((xq - xp)^2 + (yq - yp)^2)

Opgemerkt moet worden dat deze formule gelijkwaardig is aan de stelling van Pythagoras, zoals weergegeven in figuur 2.

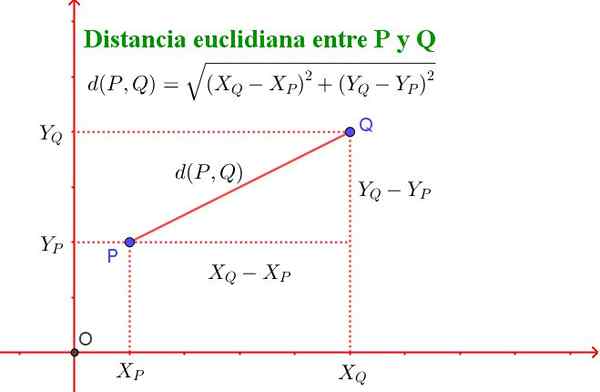Figuur 2. De afstand tussen twee punten P en Q van het vliegtuig ontmoet de stelling van Pythagoras. (Opgesteld door Ricardo Pérez).

Nonuclidiaanse oppervlakken

Niet alle twee -dimensionale ruimtes voldoen aan Euclidische geometrie. Het oppervlak van een bol is een twee -dimensionale ruimte.

De hoeken van een driehoek op een bolvormig oppervlak voegen niet 180º toe en daarmee wordt de stelling van Pythagoras niet vervuld, daarom vervult een sferisch oppervlak niet de axioomen van Euclid.

Euclidiaanse afstand in N -dimensies

Het concept van coördinaten kan worden uitgebreid tot grotere dimensies:

- In 2D-punt P heeft coördinaten (XP, YP)

- In 3-D een punt dat coördinaten heeft (XQ, YQ, ZQ)

- In 4-D Point R zal coördinaten hebben (XR, YR, ZR, WR)

- In N-D A Point P zal coördinaten hebben (P1, P2, P3, ..., PN)

Kan u van dienst zijn: bars Graph: kenmerken, waarvoor is het voor voorbeelden

De afstand tussen twee P- en Q-punten van een N-dimensionale Euclidische ruimte wordt berekend met de volgende formule:

D (p, q) = √ ((q1 - p1)^2 +(q2 - p2)^2 +… +(qn - pn)^2)

De geometrische plaats van alle punten die in een N-dimensionale Euclidische ruimte die equidists uit een ander vast P-punt (het midden) vormen, een N-dimensionale hypersfera vormen.

Hoe de Euclidische afstand te berekenen

Hieronder is de afstand tussen twee punten die zich in de Euclidiaanse drie -dimensionale ruimte bevinden, wordt berekend.

Neem aan dat punt A van Cartesiaanse coördinaten X, Y, Z gegeven door A :( 2, 3, 1) en punt B van coördinaten B :( -3, 2, 2).

U wilt de afstand tussen deze punten bepalen, waarvoor de algemene relatie wordt gebruikt:

D (a, b) = √ ((-3 - 2) 2 + (2 - 3) 2 + (2 - 1) 2) = √ ((-5) 2 + (-1) 2 + (1) 2 ))

D (a, b) = √ (25 + 1 + 1) = √ (27) = √ (9 *3) = 3 √ (3) = 5.196

Voorbeeld

Er zijn twee punten P en Q.  Het P -punt voor Cartesiaanse coördinaten x, y, z gegeven door p :( 2, 3, 1) en het punt q van coördinaten q :( -3, 2, 1).

Er wordt gevraagd om de coördinaten van het middelpunt M van het [PQ] -segment te vinden dat de twee punten verbindt. 

Oplossing:

Er wordt aangenomen dat het onbekende punt M coördinaten heeft (x, y, z).

Aangezien m gemiddeld [pq] is, moet worden vervuld dat d (p, m) = d (q, m), dus het moet ook worden vervuld d (p, m)^2 = d (q, m)^ 2:

(X - 2)^2 + (y - 3)^2 + (z - 1)^2 = (x - (-3))^2 + (y - 2)^2 + (z - 1)^2

Zoals in dit geval is de derde term hetzelfde in de twee leden, de vorige uitdrukking is vereenvoudigd om:

Kan u van dienst zijn: absolute constante

(X - 2)^2 + (y - 3)^2 = (x + 3)^2 + (y - 2)^2 

Er is dan een vergelijking met twee onbekenden x en y. Een andere vergelijking is vereist om het probleem op te lossen.

Punt M behoort tot de lijn die door de P- en Q -punten gaat, die we als volgt kunnen berekenen:

Ten eerste is de directeur Vector Pq van de lijn: Pq = = = .

Dan P.M = Op + naar Pq, waar Op Het is de vectorpositie van punt P en naar Het is een parameter die tot reële getallen hoort. 

De vorige vergelijking staat bekend als de vectorvergelijking van de lijn, die in Cartesiaanse coördinaten als volgt aannemen:

= + a =

Gelijk aan de overeenkomstige componenten zijn:

X - 2 = 2 - 5 a; En - 3 = 3 -A; Z - 1 = 0

Dat wil zeggen dat x = 4 - 5a, y = 6 - a, eindelijk z = 1.

Het wordt vervangen in de kwadratische uitdrukking die X tot Y relateert:

(4 - 5a - 2)^2 + (6 - a - 3)^2 = (4 - 5a + 3)^2 + (6 - a - 2)^2

Het is vereenvoudigd:

(2 - 5a)^2 + (3 -a)^2 = (7 - 5a)^2 + (4 - a)^2

Ontwikkelt zich nu:

4 + 25 a^2 - 20a + 9 + a^2 - 6a = 49 + 25 a^2 - 70a + 16 + a^2 - 8a

Het is vereenvoudigd en annuleert vergelijkbare termen in beide leden:

4 - 20a + 9 - 6a = 49 - 70a + 16 - 8a

Parameter A:

52 a = 49 + 16 - 4 - 9 = 52 resulterend dat a = 1.

Dat wil zeggen dat x = 4 - 5, y = 6 - 1, eindelijk z = 1.

Eindelijk verkrijgen we de Cartesiaanse coördinaten van het middelpunt M van het segment [PQ]:

M: (-1, 5, 1).

Referenties

1. Lehmann c. (1972) Analytische geometrie. Uteha.
2. Superprof. Afstand tussen twee punten. Hersteld van: superprof.is
3. UNAM. Afstand tussen gerelateerde sublineaire variëteiten. Hersteld van: Prometheus.Matem.UNAM.mx/
4. Wikipedia. Euclidiaanse afstand. Hersteld van: is.Wikipedia.com
5. Wikipedia. Euclidische ruimte. Hersteld van: is.Wikipedia.com