Hoekverplaatsing

Wat is hoekige verplaatsing?

Hij Hoekverplaatsing Het is de verandering of variatie in hoekpositie dat een object in rotatie ervaart, meestal gemeten in radialen of een andere maatregel die wordt gegeven voor bochten, zoals cijfers of revoluties.

Wanneer een object draait om een ​​vaste as, wordt de hoekverplaatsing ervan bepaald door het meten van de hoek geveegd door een lijn die door elk punt van het lichaam gaat dat de rotatieas snijdt, dat wil zeggen een radiale lijn.

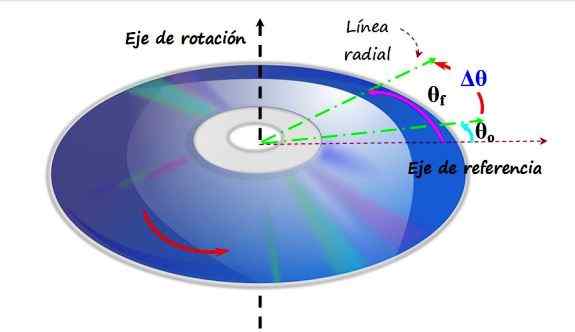Een compactschijf of CD draait in een antihoranante richting rond een verticale rotatieas. Bij het passeren van hoek θo naar θf wordt gezegd dat het een hoekige verplaatsing heeft ervaren. Bron: f. Zapata.

In de bovenste figuur is er een CD die roteert in een anti -horaire richting, als de rotatas is de verticale as. Een referentieas wordt op het vlak van de CD geplaatst, die overeenkomt met de hoek 0 radialen of 0. De groene lijn is een radiale lijn, die aanvankelijk een hoek vormt θ_of Met de referentie. Dit is uw eerste positie.

Later gaat de groene lijn naar een nieuwe positie genaamd θ_F, En de ervaren ervaring, δθ genaamd is eenvoudig:

Δθ = θ_F - θ_of

Elk punt P van de CD ervaart dezelfde hoekverplaatsing in een bepaald tijdsinterval, behalve het midden, waar de rotatieas passeert en in rust blijft.

Formules en vergelijkingen

Er is een object dat draait om een ​​vaste as of dat het scherm aan de lezer overlaat. En daarin bevindt zich punt P, gelegen op een afstand R van de rotatieas en het beschrijven van radiomoma's van radio.

Dit wordt gezien in de volgende figuur, die een snijobject toont, gezien in tegenstelling tot de kloknaalden. Het punt in kwestie is in hoekpositie θ, gemeten vanuit de referentieas, die in dit geval de horizontale as is.

Kan u van dienst zijn: additief principe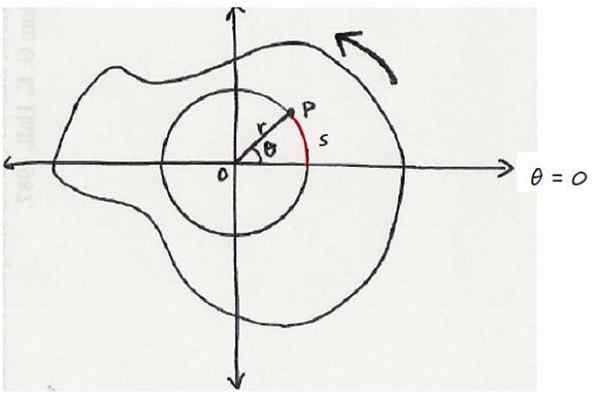Een object dat in anti -horaire zin roteert. De rotatieas staat loodrecht op het scherm. Bron: Wikimedia Commons.

Volgens het Verdrag, tot de rotatie in antihorariale zin, wordt het positief zinvol toegewezen, terwijl de rotatie in een schema een negatief teken heeft.

Terwijl het punt p de hoek θ zweert, reist het tegelijkertijd de boog s. Aangezien θ een centrale hoek is, omdat het hoekpunt het centrum van de omtrek bezet, is het vervuld dat:

Met θ uitgedrukt in radianen.

De hoekverplaatsing is:

Δθ = θ_laatste  - θ_voorletter

Als P bijvoorbeeld begon met θ_voorletter = 0 rad en is dan in θ_laatste = 0.8 RAD, de hoekige verplaatsing is van:

Δθ = 0.8 rad - 0 rad =  0.8 rad

Andere punten van het object kunnen verschillende hoekposities innemen, maar alle ervaren dezelfde hoekverplaatsing. De meest afgelegen deeltjes van het midden reizen echter grotere afstanden, aangezien S = R⋅θ.

Hoeken meet

In de rotatie is het gebruikelijk om de hoeken te vinden die in radialen worden gemeten, maar ze worden ook gevonden in graden en revoluties of beurten. In probleemoplossing is het noodzakelijk om van deze eenheden naar radianen te gaan.

1 Revolutie is gelijk aan een volledige wending, dat wil zeggen, wanneer een volledige beurt gebroken is, is deze 360 ​​º geworden en deze zijn gelijk aan 2π radialen, omdat het punt in dat geval een boog heeft getourd gelijk aan 2πr:

Maar vereenvoudiging, de eerdere gelijkwaardigheid kan als volgt worden uitgedrukt:

π radianen = 180º

Hoe wordt de hoekverplaatsing berekend?

De hoekverplaatsing kan analoog worden berekend aan hoe de verplaatsing in de beweging wordt berekend in een dimensie, volgens een bepaald bewegingsmodel. Hiervoor wordt de gemiddelde hoeksnelheid gedefinieerd als de hoekverplaatsing δθ in een gegeven tijdsinterval Δt:

Waar de gemiddelde hoeksnelheid wordt aangeduid als ω_M en wordt gegeven in radialen in eenheden van het internationale systeem als.

Kan u van dienst zijn: hoe u de hoek van een driehoek kunt krijgen? (Voorbeeld)

Directe hoeksnelheid is de limiet van de gemiddelde hoeksnelheid wanneer Δt → 0:

Dat wil zeggen, het is de eerste afgeleid van de hoekpositie ten opzichte van de tijd. Op zijn beurt kan een hoekversnelling worden gedefinieerd, aangeduid als α, die equivalent is aan de derivaat of veranderingssnelheid van hoeksnelheid ten opzichte van de tijd:

Die ook kan worden geïnterpreteerd als de tweede afgeleid van de hoekpositie ten opzichte van de tijd.

Het belangrijkste is dat twee bewegingsmodellen kunnen worden vastgesteld in analogie met de rechtlijnige bewegingen, omdat hoewel de rotaties in het vlak worden uitgevoerd, een enkele hoekcoördinaat voldoende is om de positie van elk punt van het object vast te stellen.

Uniforme cirkelvormige beweging

In de uniforme cirkelvormige beweging is de hoeksnelheid constant, dat wil zeggen, de gemiddelde hoeksnelheid is gelijk aan onmiddellijke hoeksnelheid. Aangezien hoekversnelling α gelijk is aan 0, kunt u de volgende vergelijking schrijven voor de positie als functie van de tijd:

θ = θ_of + ωt

Waar θ_of Het is de beginpositie van de mobiel.

Uniform versnelde cirkelvormige beweging

In dit geval is hoekversnelling α constant en in analogie met de uniform gevarieerde rechtlijnige beweging kunnen de volgende vergelijkingen worden geschreven:

• θ = θ_of + Ω_of T + ½ αt²
• Ω = ω_of + αT 
• Ω² = Ω_of² + 2a ∙ δθ

Oefening opgelost

Eerste oefening

Er kan worden aangenomen dat de aarde een rigide object is dat draait op een vaste as en dat de rotatie bijna uniform is. In het tijdsinterval Δt = 12 uur Zoek:

a) de hoekige verplaatsing van de aarde

b) Uw hoeksnelheid

c) hoekversnelling gedurende die tijdsinterval.

Oplossing voor

Wetende dat de aarde in 24 uur een complete draai om zijn as neemt, in 12 uur heb je de helft van een ronde gewend, dat wil zeggen π radianen. Als het wordt beschouwd als dat deel van θ_voorletter = 0 rad, dan is de hoekige verplaatsing:

Kan u van dienst zijn: multiplicatief principe: teltechnieken en voorbeelden

Δθ = π radialen

Oplossing B

Omdat rotatie uniform is, is hoeksnelheid het quotiënt tussen hoekverplaatsing en tijd, bovendien, 1 uur = 3600 s:

Ω = π rad / 12 h = π rad / (12 x 3600) s = 0.000073 RAD/S.

Oplossing C

Hoekversnelling is nietig, omdat de rotatie van de aarde uniform is.

Tweede oefening

Juan heeft een afstand van 35 meter gelopen op een cirkelvormige atletiekbaan waarvan de straal gelijk is aan 7 meter. Bereken de hoekige verplaatsing die Juan heeft gemaakt.

Oplossing

Omdat de afstand van de gereisde boog en de straal van de omtrek bekend is, kan de tweede formule worden toegepast om de hoekverplaatsing te kennen die Juan heeft gemaakt. Met behulp van de hierboven beschreven formule moet u θ = 35/7 = 5 radialen.

Derde oefening

Als Mario in zijn voertuig moet, de helft van een cirkelvormig racetraject, wat is de hoekige verplaatsing die Mario heeft gedaan?

Oplossing

In deze oefening is de eerste formule van toepassing. Omdat het bekend is dat Mario de helft van het spoor heeft gereisd, kan worden aangenomen dat hij de race in hoek 0 ° begon en toen hij de helft van de omtrek bereikte, heeft hij 180 ° gereisd. Daarom is het antwoord 180 ° -0 ° = 180 ° = π radialen.

Vierde oefening

Maria heeft een cirkelvormig zwembad. Uw hond rent rond het zwembad op een afstand van 18 meter. Als de straal van het zwembad 3 meter is, wat is dan de hoekige verplaatsing gemaakt door het huisdier van Maria?

Oplossing

Omdat het zwembad cirkelvormig is en de straal ervan bekend is, kunt u doorgaan met het gebruik van de tweede formule.

Het is bekend dat de straal gelijk is aan 3 meter en de door het huisdier afgelegd afstand is gelijk aan 18 meter. Daarom is de uitgevoerde hoekverplaatsing gelijk aan θ = 18/3 = 6 radialen.

Referenties

1. Katz, D. 2013. Natuurkunde voor wetenschappers en ingenieurs. Stichtingen en verbindingen. Cengage leren.
2. Rex, a. 2011. Fundamentals of Physics. Pearson.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Tipler, p. (2006). Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.