Ongelijkheid van de demonstratiedriang, voorbeelden, oefeningen opgelost

Het heet Ongelijkheid van de driehoek aan de eigenschap die twee reële getallen voldoet die bestaan ​​uit de absolute waarde van zijn som is altijd kleiner dan of gelijk aan de som van zijn absolute waarden. Deze eigenschap staat ook bekend als Minkowski -ongelijkheid of driehoekige ongelijkheid.

Deze eigenschap van de getallen wordt driehoekige ongelijkheid genoemd, omdat het in de driehoeken gebeurt dat de lengte van de ene kant altijd kleiner is dan of gelijk is aan de som van de andere twee, zelfs als deze ongelijkheid niet altijd van toepassing is op het gebied van driehoeken.

Figuur 1. De absolute waarde van de som van twee getallen is altijd kleiner dan of gelijk aan de som van zijn absolute waarden. (Bereid door r. Pérez)

Er zijn verschillende demonstraties van driehoekige ongelijkheid in reële getallen, maar in dit geval zullen we een kiezen op basis van de eigenschappen van de absolute waarde en de vierkante binomiale.

Stelling: Voor alle nummers naar En B Het behorend tot reële getallen, het moet:

| A + B | ≤ | A | + | B |

[TOC]

Demonstratie

We beginnen met het overwegen van het eerste lid van de ongelijkheid, dat zal worden verminderd:

| A + b |^2 = (a + b)^2 = a^2 + 2 a b + b^2 (ec. 1)

In de vorige stap is de eigenschap gebruikt dat elk getal hoog aan het vierkant gelijk is aan de absolute waarde van het genoemde getal hoog aan het vierkant, dat wil zeggen: | x |^2 = x^2. De ontwikkeling van het vierkante binomiale is ook gebruikt.

Alle nummer X Het is kleiner dan of gelijk aan zijn absolute waarde. Als het nummer positief is, is het gelijkheid waard, maar als het aantal negatief is, zal het altijd minder zijn dan een positief getal. In dit geval is zijn eigen absolute waarde, dat wil zeggen dat dat kan worden vermeld x ≤ | X |.

Kan u van dienst zijn: niet -lineaire programmering: methoden en oefeningen

Het product (A B) Het is een getal, daarom wordt dat toegepast (A b) ≤ | A B |. Wanneer deze eigenschap wordt toegepast op (EC. 1) We hebben:

| A + b |^2 = a^2 + 2 (a b) + b^2 ≤ a^2 + 2 | A B | + B^2 (EC. 2)

Overwegende dat | A B | = | A || B | LA (EC. 2) Het kan als volgt worden geschreven:

 | A + b |^2 ≤ a^2 + 2 | A || B | + B^2 (EC. 3)

Maar zoals we eerder hebben gezegd dat het kwadraat van een getal gelijk is aan de absolute waarde van het nummer hoog aan het vierkant, dan kan vergelijking 3 als volgt worden herschreven:

 | A + b |^2 ≤ | a |^2 + 2 | a | | B | + | B |^2 (EC. 4)

In het tweede lid van ongelijkheid wordt een opmerkelijk product erkend, wat wanneer toegepast leidt tot:

 | A + b |^2 ≤ (| a | + | b |)^2 (ec. 5)

In de vorige uitdrukking moet worden opgemerkt dat de waarden die op beide leden van ongelijkheid moeten worden verhoogd ook positief zijn dat ook moet worden vervuld dat:

 | A + B | ≤ (| A |+ | B |) (EC. 6)

De vorige uitdrukking is precies wat je wilde laten zien.

Voorbeelden

Vervolgens zullen we de driehoekige ongelijkheid controleren met verschillende voorbeelden.

voorbeeld 1

De waarde wordt genomen A = 2 en de waarde B = 5, dat wil zeggen beide positieve getallen en we controleren of we al dan niet aan de ongelijkheid zijn voldaan.

 | 2 + 5 | ≤ | 2 |+ | 5 |

 | 7 | ≤ | 2 |+ | 5 |

7 ≤ 2+ 5

Gelijkheid wordt geverifieerd, daarom is de stelling van de driehoeksongelijkheid vervuld.

Voorbeeld 2

De volgende waarden worden gekozen a = 2 en b = -5, dat wil zeggen een positief getal en het andere negatieve, we controleren of de ongelijkheid is voldaan.

Kan u van dienst zijn: Trinomial

 | 2 - 5 | ≤ | 2 |+ | -5 |

 | -3 | ≤ | 2 |+ | -5 |

 3 ≤ 2 + 5

Ongelijkheid wordt vervuld, daarom is de driehoekige ongelijkheidsstelling geverifieerd.

Voorbeeld 3

De waarde wordt genomen a = -2 en de waarde B = 5, dat wil zeggen een negatief getal en het andere positieve, verifiëren we of de ongelijkheid al dan niet is voldaan.

 | -2 + 5 | ≤ | -2 |+ | 5 |

 | 3 | ≤ | -2 |+ | 5 |

 3 ≤ 2 + 5

Ongelijkheid wordt geverifieerd, daarom is de stelling vervuld.

Voorbeeld 4

De volgende waarden a = -2 en b = -5 worden gekozen, dat wil zeggen, beide negatieve getallen en we controleren of we al dan niet ongelijkheid zijn voldaan.

 | -2 - 5 | ≤ | -2 |+ | -5 |

 | -7 | ≤ | -2 |+ | -5 |

 7 ≤ 2+ 5

Gelijkheid wordt geverifieerd, daarom is de Minkowsk -ongelijkheidsstelling vervuld.

Voorbeeld 5

De waarde wordt genomen A = 0 en de waarde B = 5, dat wil zeggen een nul -getal en het andere positief, dan controleren we of de ongelijkheid is voldaan.

 | 0 + 5 | ≤ | 0 |+ | 5 |

 | 5 | ≤ | 0 |+ | 5 |

 5 ≤ 0+ 5

Gelijkheid wordt vervuld, daarom is de stelling van de driehoeksongelijkheid geverifieerd.

Voorbeeld 6

De waarde wordt genomen a = 0 en de waarde b = -7, dat wil zeggen een nulnummer en het andere positief, dan controleren we of de ongelijkheid is voldaan.

 | 0 - 7 | ≤ | 0 |+ | -7 |

 | -7 | ≤ | 0 |+ | -7 |

 7 ≤ 0+ 7

Gelijkheid wordt geverifieerd, daarom is de stelling van de driehoekige ongelijkheid vervuld.

Opgeloste oefeningen

In de volgende oefeningen vertegenwoordigt geometrisch de ongelijkheid van de driehoek of ongelijkheid van minkowski voor getallen a en b.

Kan u van dienst zijn: papomudas

Het nummer A wordt weergegeven als een segment op de X -as, de oorsprong ervan of valt samen met de nul van de x -as en het andere uiteinde van het segment (op punt P) zal in de positieve richting (rechts) zijn van de x as als a> 0, maar tot < 0 estará hacia la dirección negativa del eje X, tantas unidades como indique su valor absoluto.

Evenzo zal nummer B worden weergegeven als een segment waarvan de oorsprong op punt P is. Het andere uiteinde, dat wil zeggen het punt dat rechts van P zal zijn als B positief is (b> 0) en het punt Q zal | b | eenheden links van P als B<0.

Oefening 1

Vertegenwoordigen grafisch de ongelijkheid van de driehoek voor a = 5 en b = 3 | A + B | ≤ | A | + | B |, wezen C = A + B. 

Oplossing 1: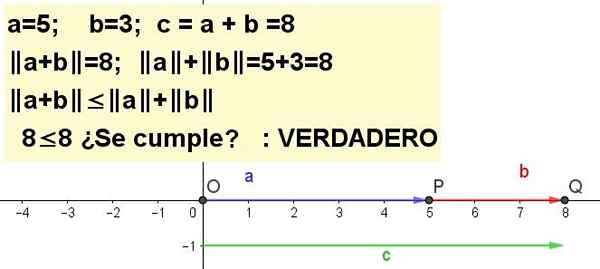

Oefening 2

Maak een driehoekige ongelijkheidsgrafiek voor a = 5 en b = -3. 

| A + B | ≤ | A | + | B |, wezen C = A + B.

Oplossing 2:

Oefening 3

Grafiek de ongelijkheid van de driehoek voor a = -5 en b = 3.

| A + B | ≤ | A | + | B |, wezen C = A + B. 

Oplossing 3: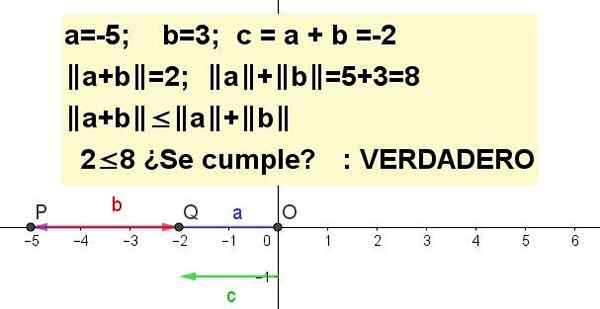

Oefening 4

Grafiek de driehoekige ongelijkheid voor A = -5 en B = -3.

| A + B | ≤ | A | + | B |, wezen C = A + B.

Oplossing 4: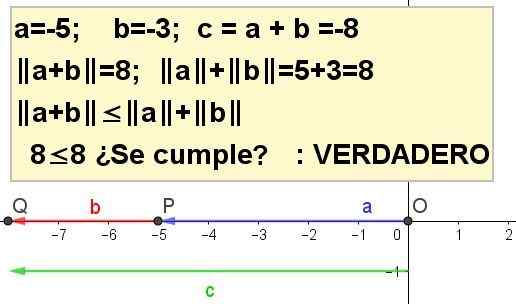

Referenties

1. EN. Whitesitt. (1980).Booleaanse algebra en zijn toepassingen . Continentaal redactioneel bedrijf C. NAAR.
2. Mícheal of 'searcoid.(2003) Elementen van abstracte analyse ... Afdeling Wiskunde. University College Dublin, Beldfield, Dublind.
3. J. Van Wyk. (2006) Wiskunde en engineering in informatica. Instituut voor computerwetenschappen en technologie. National Bureau of Standards. Washington, D. C. 20234
4. Eric Lehman. Wiskunde voor informatica.  Google Inc.
5. F Thomson Leighton (1980). Calculus. Afdeling Wiskunde en de Computer Science and AI Laboratory, Massachussetts Institute of Technology.
6. Khan Academy. Triangle ongelijkheid stelling. Hersteld van: Khanacademy.borg
7. Wikipedia. Driehoekige ongelijkheid. Hersteld van: is. Wikipedia.com