Hoeveel diameters heeft een omtrek?

Een omtrek heeft oneindige diameters. Het is gemakkelijk om te zien dat het zo is, als het is gebaseerd op de definitie van diameter, het segment dat tegelijkertijd door het midden van de omtrek gaat en met twee punten daarvan.

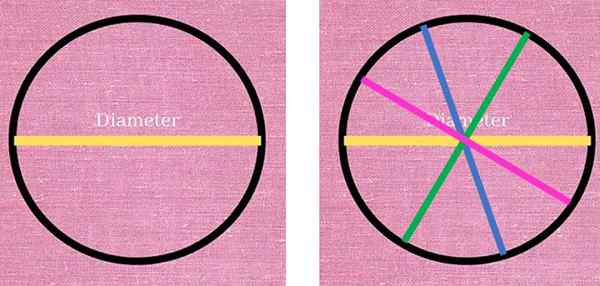
In de volgende figuur, links, wordt de gele lijn die overeenkomt met een diameter van de omtrek waargenomen en verdeeld in twee delen. Aan de rechterkant werden drie andere diameters in verschillende kleuren getekend: blauw, groen en roze. Allen hebben dezelfde lengte en voldoen aan de toestand van het samenvoegen van twee punten van de omtrek, door het midden van hetzelfde.

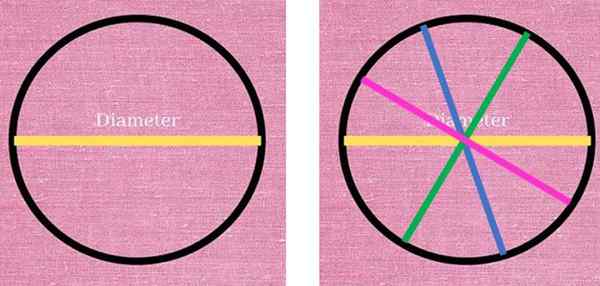De diameter is een onderscheidend segment, dat altijd door het midden van de omtrek gaat en twee punten hiervan verbindt. Aan de linkerkant verdeelt de gele diameter de omtrek in twee. Aan de rechterkant zijn er andere diameters die ook de omtrek in twee helften verdelen. Bron: f. Zapata.

Zoals te zien is, zijn de mogelijkheden om diameters te tekenen eindeloos, omdat oneindig de punten zijn die de omtrek vormen. Hetzelfde kan worden bevestigd over de straal, het segment dat elk punt van de omtrek met het centrum verenigt: een oneindig aantal radio's kan worden getrokken.

En bij het plaatsen van twee tegenovergestelde radio's van elkaar, wordt een diameter verkregen, omdat de straal de helft hiervan meet.

Diameter, radio- en omtreklengte

Of het nu de diameter van elke omtrek en r, zijn straal is. Aangezien de diameter twee keer zoveel meet als de radio, kan deze worden geschreven:

D = 2 ∙ r

Het betekent dat, als de straal van een cirkel bijvoorbeeld r = 5 cm is, de diameter ervan d = 2 ∙ 5 cm = 10 cm is.

Het kan u van dienst zijn: Fibonacci -serie: eigenschappen, natuurlijke relaties, toepassingen

De diameter staat ook bekend als de Groot touw. De snaren zijn lijnen of segmenten die worden getrokken tussen twee punten van de omtrek, maar die niet noodzakelijkerwijs door het centrum gaan. Alleen de diameter heeft dat onderscheid.

In de volgende figuur kunt u het verschil zien en zien waarom de diameter (rood) in feite de grootste van de snaren is die op de omtrek kunnen worden getrokken:

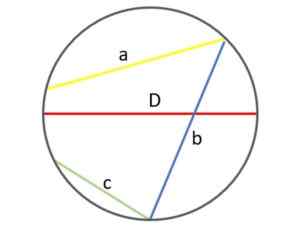Verschillende touwen in een omtrek: de diameter is de grootste van allemaal. Bron: f. Zapata.

Natuurlijk is de diametermaat (en dus de straal) hetzelfde in een bepaalde omtrek. Bij variërend wordt een kleinere of grotere omtrek verkregen, volgens.

Aan de andere kant varieert de grootte van de snaren van dezelfde omtrek, afhankelijk van hoe ver of nabij de punten de punten zijn die zich aansluiten. In het getoonde voorbeeld is het groene "C" -touw ogenschijnlijk korter dan de "A" en "B" Strings.

En het aantal tekenreeksen is ook oneindig.

De omtrek van de omtrek

Van zijn kant is de lengte van de omtrek gelijk aan zijn omtrek of contour. Het is gerelateerd aan zijn diameter, omdat hoe hoger dit, hoe groter de omtrek (de omtrek is groter).

De verhouding of quotiënt tussen perimeter en diameter is een constante genaamd π (leest "pi"). De waarde van π is 3.141592 ... De suspensieve punten geven aan dat de hoeveelheid decimalen en oneindig, dat komt omdat PI een irrationeel aantal is. Voor praktische doeleinden kan PI echter eenvoudigweg 3 afronden.14

Kan u van dienst zijn: hoeveel moet u toevoegen aan 3/4 om 6/7 te krijgen?

Als de perimeter wordt aangeduid als C en de diameter als D, wordt deze reden als volgt verhoogd:

C / d = π

Daarom is de formule voor de lengte van de omtrek:

C = π ∙ D

Of indien de voorkeur gebaseerd op straal R:

C = 2π ∙ r

Illustratief voorbeeld

De afbeelding toont drie identieke omtrek, aangewezen met letters A, B en C. In elk van de mier loopt de mier de weg op de blauwe kleurensegmenten, om van het ene punt naar het andere van de omtrek te gaan.

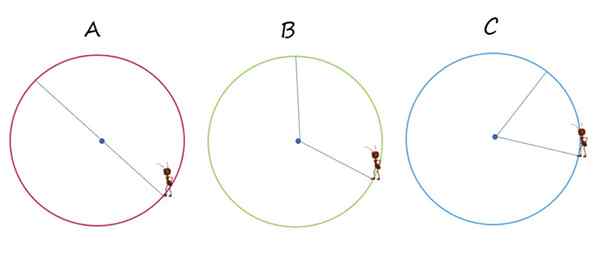De mier beweegt van het ene punt naar het andere van de omtrek door de dunste blauwe lijnen. Bron: f. Zapata.

1.- In welke van de gevallen komt de verplaatsing precies op de diameter van de omtrek?

Antwoord

Alleen in geval A, omdat dat pad door het midden van de omtrek gaat en van het ene punt naar het andere van hetzelfde gaat.

2.- Hoeveel radio's reist het insect in elk geval?

Antwoord

In een van de drie gevallen reist de mier twee radio's van de omtrek.

3.- Welke van de paden komt overeen met de grootste afstand?

Antwoord

De reis is in elk geval even lang, gelijk aan twee radio's van de omtrek.

4.- In welk geval de mier verder weg is van het startpunt?

Antwoord

In geval A, omdat het op het punt is dat er precies voor staat, in de resterende, is de mier dichter bij het startpunt.

5.- En in welk geval de mier eindigt dat de route dichter bij het punt van oorsprong is?

Kan u van dienst zijn: tekenen van groepering

Antwoord

In het geval C.

6.- Als de straal van de omtrek 20 cm is, hoeveel centimeter meet dan elke route?

Antwoord

Omdat de mier een afstand loopt die gelijk is aan twee radio's, is de totale afgelegde afstand 40 cm.

Opgeloste oefeningen

Oefening 1

Bereken de straal van een cirkel waarvan de diameter 4 is.5m.

Oplossing

De radio is de helft van de diameter, als dit 4 meet.5 cm, dan is Radio R 2.25 cm.

Oefening 2

Vind de omtrek van de omtrek van oefening 1.

Oplossing

De perimeter wordt berekend door de diameter of door de straal, zoals voorkeur. In het eerste geval:

C = π ∙ D

Ervan uitgaande dat π = 3.14 tot rond, de vervanging van waarden geeft het volgende resultaat:

C = π ∙ d = 3.14 ∙ 4.5 cm = 14.13 cm

Oefening 3

Een ontwerper wordt gevraagd om een ​​hartvormig logo te tekenen, met de afmetingen aangegeven in de figuur. De gebogen delen komen overeen met exacte semicircums.

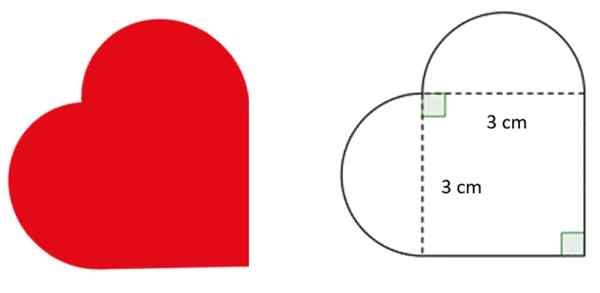
Met dit informatie antwoord:

1. Wat is de straal van de halve circuits?
2. Hoeveel is de omtrek van het hart?

Oplossing voor

De diameter van de halfcircerenties is gelijk aan de zijkant van het vierkant, dat is 3 cm. Daarom meet de straal, die de helft is, 1.5 cm.

Oplossing B

De omtrek van de hartvormige figuur is de som van de twee buitenste zijden van het vierkant en de omtrek van de semi -cunances. Zoals identiek zijn, is de omtrek ervan gelijk aan die van een volledige cirkel met diameter 3 cm:

C = π ∙ d = 3.14 ∙ 3 cm = 9.42 cm

Daarom is de omtrek P van de figuur:

P = 9.42 cm + 3 cm + 3 cm = 15.42 cm