Hoeveel is X door X?

Vermenigvuldigen x door x je krijgt x².

X² leest als "X Squared" Of gewoon "X Squared".

Waarom X door X X is²?

Het resultaat van X door X is X².

Het is een heel eenvoudig resultaat om te verifiëren, dankzij de Eigenschap van de vermenigvuldiging van krachten van gelijke basis.

In algebra wordt de letter X gebruikt als een manier om een ​​bedrag aan te roepen dat onbekende waarden aanneemt, hoewel andere letters ook kunnen worden gebruikt.

De eigenschap van de vermenigvuldiging van bevoegdheden van dezelfde basis stelt dat "Bij het vermenigvuldigen van twee identieke basen wordt dezelfde basis geschreven en worden de exponenten toegevoegd".

X^naar∙ x^B = x^A+B

De exponent gelijk aan 1 van de X wordt meestal weggelaten, zodat X¹ = x.

Als we willen weten hoeveel x door x:

De Basis is x (hetzelfde is geschreven) en Exponenten worden toegevoegd aan+B (De waarden zijn gelijk aan 1):

x ∙ x = x¹⁺¹ = x²

Voorbeelden van de eigenschap van de vermenigvuldiging van krachten van gelijke basis

Laten we eens kijken naar enkele zeer eenvoudige numerieke voorbeelden:

2 × 2 = 2² = 4

3 × 3 = 3² = 9

4 × 4 = 4² = 16

(−2) × (−2) = 2² = 4

Merk op dat het negatieve teken hierboven het resultaat niet verandert, omdat volgens de wet van tekenen, het vermenigvuldigen van twee negatieve hoeveelheden worden verkregen positief resultaat.

In de vorige voorbeelden werden hele getallen gebruikt, maar de bewerking is even geldig voor decimalen, fractionele, reële en complexe getallen.

Het gebied van een vierkant

Het kwadraat van een getal verschijnt vaak bij de berekening van gebieden met reguliere geometrische figuren. Bijvoorbeeld die van het vierkant, dat een enkele vierzijdige polygoon is, die allemaal dezelfde maat hebben.

Kan u van dienst zijn: Systeem van vergelijkingen: oplossingsmethoden, voorbeelden, oefeningen

Het gebied van een vierkant wordt gegeven door het vierkant van zijn zijde, als het "x" wordt genoemd, dan is gebied A van het vierkant waard x².

Voorbeeld van het gebied van een vierkant

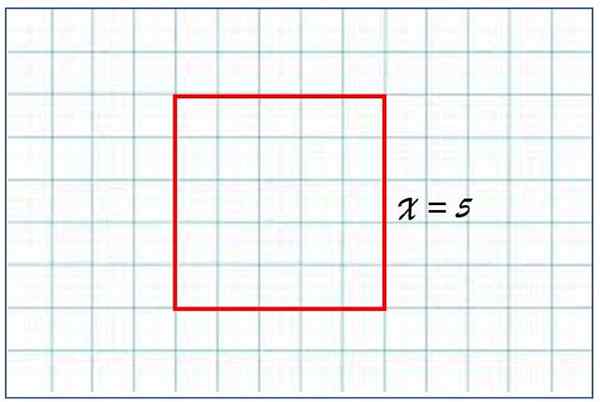
Vierkant gebied A waarvan de zijde x = 5 eenheden is, is gelijk aan:

A = 5² = 5 × 5 = 25 gebiedseenheden

Een vierkant aan de zijkant gelijk aan 5 willekeurige lengte -eenheden heeft een oppervlakte van 25 eenheden gebied. Bron: f. Zapata.

Dit resultaat is logisch, omdat het vierkant bestaat uit 5 rijen en 5 kolommen van kleinere vierkanten, van de zijkant gelijk aan 1. Als de lezer de figuur zorgvuldig observeert, zal hij zich realiseren dat het rode vierkant uit 25 kleine vierkanten van eenheidsgebied bestaat.

Belangrijk:

De eenheden in dit voorbeeld zijn willekeurig, ze kunnen meters, centimeters, inches of andere zijn. Hier waren ze niet gespecificeerd, maar in elk geval zou het respectieve gebied worden gegeven in meters kwadraat, vierkante inches of andere. Het gebied wordt altijd gegeven in eenheden van vierkante lengte.

Het kwadraat van fractionele en decimale getallen

Om het vierkant van een fractioneel getal te vinden, een dat bestaat uit een genummerde en een noemer, gescheiden door de breuklijn, is het noodzakelijk om de teller met zichzelf te vermenigvuldigen, evenals de noemer, die een nieuw fractioneel nummer verkrijgt.

Voorbeelden van vierkante nummers vierkanten

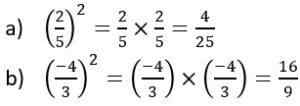
Voorbeelden van vierkante nummers

Wat betreft het kwadraat van een decimaal nummer, we moeten de regels van vermenigvuldiging volgen voor decimale getallen.

A) 0.6² = 0.6 × 0.6 = 0.36

b) (−0.4)² = (−0.4) × (−0.4) = 0.16

Zowel in dit voorbeeld als in de overeenkomstige van de vorige sectie worden waargenomen dat het kwadraat van een negatief getal altijd positief is. Dit geldt voor de gelijkmatige krachten, niet alleen voor het plein.

Kan u van dienst zijn: equivalente sets: wat zijn, uitleg, voorbeelden