Wat zijn de gewichtswetten van chemie? (Voorbeelden)

De Toeste wetten van chemie Zij zijn degenen die hebben aangetoond dat de massa's van de stoffen die reageren dit niet willekeurig of willekeurig doen; maar het handhaven van een constant wiskundig aandeel van hele getallen of ondermijnijten van hen, waarin de atomen van de elementen niet worden gecreëerd of vernietigd.

In het verleden vereiste het vaststellen van deze wetten buitengewone redeneringsinspanningen; Want hoewel het nu te duidelijk lijkt, voordat de atoom- of moleculaire massa's van de elementen of verbindingen niet eens bekend waren,.

Bron: Jeff Keyzer uit Austin, TX, VS [CC BY-SA 2.0 (https: // creativeCommons.Org/licenties/by-sa/2.0)]

Omdat het niet bekend was hoe precies een mol atomen van elk element equivalent waren, moesten de chemicaliën van de achttiende en negentiende eeuw gebaseerd zijn op de reagerende massa's. Zodat rudimentaire analytische schalen (superieure afbeelding) onafscheidelijke metgezellen waren tijdens de honderden experimenten die nodig zijn voor de afwikkeling van de wegingswetten.

Het is om deze reden dat wanneer deze wetten van chemie worden bestudeerd, ze op elk moment massiemetingen tegenkwamen. Dankzij dit, het extrapoleren van de resultaten van de experimenten, werd ontdekt dat chemische verbindingen Zuiver Ze vormen altijd met hetzelfde massale deel van hun samenstellende elementen.

[TOC]

Wet van behoud van massa

Deze wet zegt dat in een chemische reactie de totale massa van de reagentia gelijk is aan de totale massa van de producten; Zolang het beschouwde systeem gesloten is en er geen massa -uitwisseling en energie is met zijn omgeving.

In een chemische reactie verdwijnen stoffen niet, maar worden omgezet in andere stoffen van gelijke massa; Van daaruit de beroemde uitdrukking: "Niets wordt gemaakt, er wordt niets vernietigd, alles wordt getransformeerd".

Historisch gezien werd de wet van massabesparing in een chemische reactie voor het eerst voorgesteld in 1756 door Mikhail Lomonsov, die in zijn dagboek de resultaten van zijn experimenten liet zien.

Vervolgens presenteerde Antoine Levoisier, een Franse chemicus, in 1774 de resultaten van zijn experimenten die dit mochten vaststellen; die, sommigen noemen het ook de wet van Lavoisier.

-Lavoisier -experimenten

In de tijd van Lavoisier (1743-1794) was er de theorie van Flogisto, volgens welke de lichamen het vermogen hadden om te ontstoken of te verbranden. Lavoisier -experimenten mochten deze theorie weggooien.

Lavoisier voerde talloze metaalverbrandingsexperimenten uit. Hij woog zorgvuldig de materialen voor en na zijn verbranding in een gesloten container, en ontdekte dat er een duidelijke gewichtstoename was.

Maar lavoiser, gebaseerd op de kennis van de rol van zuurstof in verbranding, concludeerde dat de gewichtstoename in verbranding te wijten was aan de opname van zuurstof in verbrandingsmateriaal. Het concept van metaaloxiden werd geboren.

Daarom bleef de som van de massa's van de metalen die werden onderworpen aan verbranding en zuurstof onveranderlijk gebleven. Deze conclusie stond de oprichting van de massa -natuurbeschermingswet toe.

-Balancing van vergelijkingen

De massa -natuurbeschermingswet heeft de noodzaak vastgesteld om chemische vergelijkingen in evenwicht te brengen en te garanderen dat het aantal van alle elementen die betrokken zijn bij een chemische reactie, evenals reagentia of producten, exact hetzelfde is.

Dit is een essentiële vereiste voor de nauwkeurigheid van de stoichiometrische berekeningen die worden gemaakt.

-Berekeningen

Mol water

Hoeveel mol water kan optreden tijdens de verbranding van 5 mol methaan in een overtollige zuurstof? Toont ook aan dat de wet van het behoud van materie is vervuld.

Ch₄   +    2 O₂   => CO₂   +    2 H₂OF

Als we de evenwichtige vergelijking van de reactie waarnemen, wordt geconcludeerd dat 1 mol methaan 2 mol water produceert.

Het probleem kan direct worden opgelost met een eenvoudige aanpak, omdat we geen 1 mol maar 5 mol cho hebben₄:

Mol water = 5 mol cho₄· (2 mol h H₂O / 1 mol Cho₄))

= 10

Wat zou gelijkwaardig zijn aan 180 g h h₂OF. 5 mol of 220 g CO werd ook gevormd₂, die gelijk is aan een totale massa van 400 g producten.

Aldus voor de wet van het behoud van het onderwerp om 400 g reagentia te reageren; niet meer niet minder.  Van die 400 g komt 80 g overeen met de 5 mol Cho₄ (vermenigvuldigen met zijn moleculaire massa van 16 g/mol) en 320 g bij 10 mol O O₂ (Evenzo vanwege de moleculaire massa van 32 g/mol).

Verbranding van een magnesiumtape

Een magnesiumband van 1,50 g verbrand in een gesloten container met 0,80 g zuurstof. Na verbranding zat 0,25 g zuurstof in de container. a) welke zuurstofmassa reageerde? b) Hoeveel magnesiumoxide is gevormd?

Kan u van dienst zijn: hypotone oplossing: componenten, voorbereiding, voorbeelden

De zuurstofmassa die reageert, wordt verkregen door een eenvoudig verschil.

Zuurstofmassa verbruikt = (initiële massa - restmassa) zuurstof

= 0,80 g - 0,25 g

= 0,55 g of₂ (naar)

Volgens de massa -behoudswet,

Magnesiumoxidemassa = magnesiummassa +zuurstofmassa

= 1,50 g + 0,55 g

= 2,05 g mgo (b)

Wet van duidelijke verhoudingen

Joseph Louis Proust (1754-1826), de Franse chemicus, realiseerde zich dat in een chemische reactie de chemische elementen altijd reageren in verhoudingen met een vaste massa om een ​​verbinding te vormen zuiver specifiek; Daarom is de samenstelling ervan constant, ongeacht de bron of oorsprong, of hoe deze wordt gesynthetiseerd.

Proust in 1799 verklaarde de wet van de gedefinieerde verhoudingen, die stelt dat: "wanneer twee of meer elementen worden gecombineerd om een ​​verbinding te vormen, doen ze dit in een vaste massa -relatie". Deze relatie is dus vast en hangt niet af van de strategie die wordt gevolgd voor de voorbereiding van de verbinding.

Deze wet staat ook bekend als de wet van constante samenstelling, die stelt dat: "Elke chemische verbinding in zuiverheid bevat altijd dezelfde elementen, in een constant deel van de massa".

-Illustratie van de wet

IJzer (geloof) reageert met zwavel (en) om ijzersulfide (FES) te vormen, drie situaties kunnen worden aangegeven (1, 2 en 3):

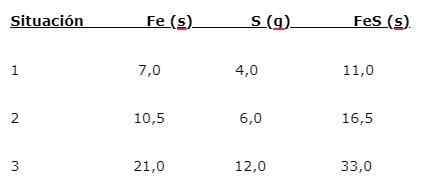
Om het aandeel te vinden waarin de elementen worden gecombineerd, wordt de belangrijkste massa (geloof) gedeeld door de kleine massa (s). De berekening geeft een deel van 1,75: 1. Deze waarde wordt herhaald in de drie gegeven voorwaarden (1, 2 en 3), waarbij hetzelfde aandeel wordt verkregen, hoewel verschillende massa's worden gebruikt.

Dat wil zeggen dat 1,75 g geloof wordt gecombineerd met 1,0 g S om 2,75 g FES te geven.

-Toepassingen

Via de aanvraag deze wet kunt u precies de massa weten van de elementen die moeten worden gecombineerd om een ​​gewenste massa van een compound te verkrijgen.

Op deze manier kan informatie worden verkregen over informatie over de overgebleven massa van een van de elementen die betrokken zijn bij een chemische reactie, of als er een beperkend reagens in de reactie is.

Bovendien is het van toepassing om de centesimale samenstelling van een verbinding te kennen, en op basis van de laatste kan de formule van een verbinding worden vastgesteld.

Centesimale samenstelling van een verbinding

Koolstofdioxide (CO₂) wordt gevormd in de volgende reactie:

C +O₂     => CO₂

12 g koolstof 32 g zuurstof wordt gecombineerd om 44 g kooldioxide te geven.

Het koolstofpercentage is dus gelijk aan

Koolstofpercentage = (12 g / 44 g) · 100 %

= 27,3 %

Zuurstofpercentage = (32 g / 44 g) · 100 %

Zuurstofpercentage = 72,7 %

Met behulp van de verklaring van de wet van constante samenstelling kan worden opgemerkt dat koolstofdioxide altijd wordt gevormd door 27,3 % koolstof en 72,7 % zuurstof.

-Berekeningen

Zwaveltrioxide

Door te reageren in verschillende containers 4 g en 6 g zwavel (s) met zuurstof (O), werden ze respectievelijk, 10 g en 15 g zwaveltrioxide verkregen (dus dus₃)).

Waarom waren zulke hoeveelheden zwaveltrioxide en niet andere?

Bereken ook de hoeveelheid zwavel die nodig is om te combineren met 36 g zuurstof en het verkregen zwaveltrioxide -deeg.

Deel a)

In de eerste container wordt 4 g g zuurstof gemengd om 10 g trioxide te verkrijgen. Als de massa -natuurbeschermingswet wordt toegepast, kunnen we de zuurstofmassa wissen die is gecombineerd met zwavel.

Zuurstofmassa = 10 g zuurstoftrioxide - 4 g zwavel.

= 6 g

In container 2 6 g zwavel worden gemengd met x g zuurstof om 15 zwaveltrioxide te verkrijgen.

Zuurstofmassa = 15 g zwaveltrioxide - 6 g zwavel

= 9 g

De verhoudingen van O/s voor elke container worden vervolgens berekend:

Aandeel o / s in situatie 1 = 6 g o / 4 g s

= 1.5 / 1

Aandeel o / s in situatie 2 = 9 g o / 6 g s

= 1.5 / 1

Die, overeenkomt met wat er in de wet wordt verhoogd van de gedefinieerde verhoudingen die aangeven dat de elementen altijd in dezelfde verhouding worden gecombineerd om een ​​bepaalde verbinding te vormen.

Daarom zijn de verkregen waarden correct en die die overeenkomen met de toepassing van de wet.

Deel B)

In de vorige sectie werd een waarde van 1,5 / 1 berekend voor het aandeel van O / S.

Kan u van dienst zijn: staat van aggregatie van materie

G van zwavel = 36 zuurstof · (1 g zwavel / 1,5 g zuurstof)

= 24 g

G van zwaveltrioxide = 36 g zuurstof + 24 g zwavel

= 60 g

Chloor en magnesium

Chloor en magnesium worden gecombineerd in het aandeel van 2,95 g chloor voor elke g magnesium. a) Bepaal de massa's chloor en magnesium die nodig is om 25 g magnesiumchloride te verkrijgen. b) Wat is de percentage samenstelling van magnesiumchloride?

Deel a)

Op basis van de 2,95 -waarde voor de CL -verhouding: MG kan de volgende aanpak worden gegeven:

2,95 g Cl +1 g mg => 3,95 g mgcl₂

Dan:

G van Cl = 25 g Mgcl₂ · (2,95 g CL / 3,95 g mgcl₂))

= 18.67

G van mg = 25 g mgcl₂ · (1 g mg / 3,95 g mgcl₂))

= 6.33

Vervolgens worden 18,67 g chloor gecombineerd met 6,33 g magnesium om 25 g magnesiumchloride te produceren.

Deel B)

De moleculaire massa van magnesiumchloride, MGCL wordt eerst berekend₂:

Mgcl molecuulgewicht₂ = 24,3 g/mol + (2 · 35,5 g/mol)

= 95,3 g/mol

Magnesiumpercentage = (24,3 g / 95,3 g) x 100 %

= 25,5 %

Chloorpercentage = (71 g / 95,3 g) x 100 %

= 74,5 %

Wet van meerdere verhoudingen of wet van Dalton

De wet werd in 1803 vermeld door de Franse chemicus en meteoroloog John Dalton, gebaseerd op zijn waarnemingen met betrekking tot de reacties van atmosferische gassen.

De wet werd als volgt vermeld: "Wanneer elementen worden gecombineerd om meer dan één verbinding te geven, sluit een variabele massa van de een van hen zich aan bij een vaste massa van de andere en de eerste heeft een relatie tussen canons en onduidelijke getallen".

Ook: "Wanneer twee elementen worden gecombineerd om verschillende verbindingen te veroorzaken, gezien een vaste hoeveelheid van hen, zijn de verschillende hoeveelheden van het andere element die worden gecombineerd met dat vaste bedrag om de verbindingen te produceren, in verband met eenvoudige hele getallen".

John Dalton maakte de eerste moderne beschrijving van het atoom als een onderdeel van de chemische elementen, toen hij erop wees dat de elementen worden gevormd door ondeelbare deeltjes die atomen worden genoemd.

Bovendien stelde hij dat de verbindingen worden gevormd wanneer atomen van verschillende elementen met elkaar samenkomen in verhoudingen van eenvoudige gehele getallen.

Dalton voltooide de onderzoekswerken van Proust. Hij wees op het bestaan ​​van twee tinoxiden, met percentages van 88,1% en 78,7% tin met de overeenkomstige percentages van zuurstof, respectievelijk 11,9% en 21,3%.

-Berekeningen

Water- en waterstofperoxide

Laat zien dat waterverbindingen, h₂Of, en waterstofperoxide, h₂OF₂, Ze voldoen aan de wet van meerdere verhoudingen.

Atomische gewichten van de elementen: H = 1 g/mol en zuurstof = 16 g/mol.

Moleculaire peso van de verbindingen: h₂O = 18 g/mol en h₂OF₂ = 34 g/mol.

Waterstof is het element met een vaste hoeveelheid in h₂Of en h₂OF₂, Dus de verhoudingen tussen O en H zullen in beide verbindingen worden vastgesteld.

O/H -verhouding in H₂O = (16 g/mol)/(2 g/mol)

= 8/1

O/H -verhouding in H₂OF₂ = (32 g/mol)/(2 g/mol)

= 16/1

Relatie tussen beide verhoudingen = (16/1)/(8/1)

= 2

Vervolgens is de verhouding van de OR/H tussen waterstofperoxide en water 2, een geheel getal en eenvoudig aantal. Er is aangetoond dat de wet van meerdere verhoudingen wordt gedemonstreerd.

Stikstofoxiden

Welke zuurstofmassa wordt gecombineerd met 3,0 g stikstof in a) stikstofoxide, NO en B) stikstofdioxide, nee₂. Laat zien dat nee en nee₂ Ze voldoen aan de wet van meerdere verhoudingen.

Stikstofmassa = 3 g

Atoomgewichten: stikstof, 14 g/mol en zuurstof, 16 g/mol.

Berekeningen

In het nee wordt een atoom van N gecombineerd met 1 atoom van O, zodat de zuurstofmassa die wordt gecombineerd met 3 g stikstof kan worden berekend door de volgende benadering:

G van o = g stikstof · (PA. O / pa. N)

= 3 g · (16 g/mol/14 g/mol)

= 3,43 g of

In het nee₂, Een atoom van N wordt gecombineerd met 2 atomen van O, dus de gecombineerde massa zuurstof is:

g zuurstof = 3 g · (32 g/mol/14 g/mol)

= 6,86 g of

Aandeel o/ n bij NO = 3,43 g o/ 3 g n

= 1,143

Verhouding of/n in nee₂ = 6,86 g o / 3 g n

= 2,282

Waarde van de relatie tussen verhoudingen O / N = 2.282 / 1.143

= 2

Vervolgens is de waarde van de relatie tussen de verhoudingen of/n 2, een geheel getal en eenvoudig nummer. Daarom is de wet van meerdere verhoudingen vervuld.

Wet van wederzijdse proporties

Deze wet geformuleerd door Richter en Carl F. Wenzel gescheiden.

Kan u van dienst zijn: natrium: geschiedenis, structuur, eigenschappen, risico's en gebruik

Als u bijvoorbeeld de twee verbindingen AB en CB hebt, wordt opgemerkt dat het gemeenschappelijke element B is.

De wet of wederzijdse proporties van Richter-Wenzel zegt dat, wetende hoeveel van een reageert met B om AB te geven, en hoeveel C reageert met B om CB te geven, u de massa kunt berekenen waarvan het nodig is om met een C-massa te reageren voor Mac.

En het resultaat is dat de verhouding tot: c of a/c een meervoudige of onderbouwing van a/b of c/b moet zijn. Deze wet wordt echter niet altijd vervuld, vooral wanneer de elementen verschillende oxidatietoestanden presenteren.

Van alle gewichtswetten is dit misschien wel de meest "abstracte" of ingewikkeld. Maar als het vanuit een wiskundig oogpunt wordt geanalyseerd, is het te zien dat alleen bestaat uit conversie- en annuleringsfactoren.

-Voorbeelden

Methaan

Als bekend is dat 12 g koolstof reageert met 32 ​​g zuurstof om koolstofdioxide te vormen; en dat aan de andere kant 2 g waterstof reageert met 16 g zuurstof om water te vormen, dan kunnen de massa -verhoudingen c/o en h/of voor de CO worden geschat₂ en h₂Of, respectievelijk.

Het berekenen van c/o en h/of u hebt:

C / o = 12 g C / 32G of

= 3/8

H / O = 2G H / 16G of

= 1/8

Zuurstof is het gemeenschappelijke element en het is gewenst te weten hoeveel koolstof reageert met waterstof om methaan te produceren; Dat wil zeggen, u wilt c/h (of h/c) berekenen. Dan is het noodzakelijk om een ​​verdeling van de vorige verhoudingen te maken om aan te tonen of de wederkerigheid is vervuld of niet:

C/h = (c/o)/(h/o)

Merk op dat op deze manier het besturingssysteem wordt geannuleerd en C/H blijft bestaan:

C/h = (3/8)/(1/8)

= 3

En 3 is een 3/8 meerdere (3/8 x 8). Dit betekent dat 3 g C reageert met 1 g H om methaan te geven. Maar om het te kunnen vergelijken met de CO₂, Het wordt C/H vermenigvuldigd met 4, die gelijk is aan 12; Dit geeft 12 g C die reageert met 4 g H om methaan te vormen, wat ook waar is.

Magnesiumsulfide

Als bekend is dat 24 g magnesium reageert met 2 g waterstof om magnesiumhydride te vormen; En bovendien reageert 32 g zwavel met 2 g waterstof om waterstofsulfide te vormen, het gemeenschappelijke element is waterstof en wil mg/s berekenen van mg/h en h/s.

Vervolgens heb je mg/h en h/s afzonderlijk berekenen:

Mg / h = 24 g mg / 2g h

= 12

H / s = 2g H / 32G S

= 1/16

Het is echter handig om S/H te gebruiken om h te annuleren. Daarom is S/H gelijk aan 16. Dit gedaan, we gaan verder met het berekenen van mg/s:

Mg/s = (mg/h)/(s/h)

= (12/16)

= 3/4

En 3/4 is een submultiple van 12 (3/4 x 16). Het mg/s -aandeel geeft aan dat 3 g mg reageert met 4 g zwavel om magnesiumsulfide te vormen. U moet Mg/S echter met 8 vermenigvuldigen om het te kunnen vergelijken met Mg/H. Aldus reageert 24 g mg met 32 ​​g zwavel om dit metalen sulfide te geven.

Aluminiumchloride

Het is bekend dat 35,5 g CL reageert met 1 g H om HCl te vormen. Ook reageert 27 g Al met 3 g h om ALH te vormen₃. Bereken het aandeel aluminiumchloride en zeg of een dergelijke verbinding de wet van Richter-Wenzel gehoorzaamt.

Nogmaals, Cl/H en AT/H worden afzonderlijk berekend:

Cl / h = 35,5 g cl / 1g h

= 35.5

AT/ H = 27G AT/ 3G H

= 9

Nu wordt het berekend op/Cl:

At/cl = (al/h)/(cl/h)

= 9/35.5

≈ 0,250 of 1/4 (het is eigenlijk 0,253)

Dat wil zeggen, 0,250 g Al reageert met 1 g CL om het overeenkomstige zout te vormen. Maar nogmaals, het moet worden vermenigvuldigd met/CL met een nummer dat het mogelijk maakt om het te vergelijken (voor comfort) met AL/H.

Indieningen in de berekening

Het wordt vervolgens vermenigvuldigd met/Cl met 108 (0,27/250), waardoor 27 g reageert met 108 g CL. Dit gebeurt niet precies zo. Als we bijvoorbeeld de 0,253 -waarde nemen door AL/CL, en we deze vermenigvuldigen met 106,7 (27/0,253), reageert 27 g AL met 106,7 g CL; Wat het meer nadert naar de realiteit (alcl₃, met een PA van 35,5 g/mol voor de CL).

Hier wordt waargenomen hoe de wet van Richter kan beginnen te wankelen vanwege precisie en misbruik van decimalen.

Referenties

1. Whitten, Davis, Peck & Stanley. (2008). Scheikunde. (8e ed.)). Cengage leren.
2. Bloemen, j. Chemistry (2002). Santillana redactioneel.
3. Joaquín San Frutos Fernández. (S.F.)). Het gewicht en de volumetrische wetten. Hersteld van: Encina.pntisch.MEC.is
4. Toppr. (S.F.)). Wetten van chemische combinatie. Hersteld van: toppr.com
5. Briljant. (2019). Wetten van chemische combinatie. Hersteld van: briljant.borg
6. Chemistry Libhethexts. (15 juli 2015). Fundamentele chemische wetten. Hersteld van: chem.Librhetxts.borg
7. Helmestine, Anne Marie, pH.D. (18 januari 2019). Wet van behoud van massa. Hersteld van: Thoughtco.com