Vierhoekige elementen, eigenschappen, classificatie, voorbeelden

A vierhoek Het is een vierzijdige polygoon en vier hoekpunten. Hun tegenovergestelde kanten Zij zijn degenen die geen gemeenschappelijke hoekpunten hebben, terwijl ze dat zijn opeenvolgende partijen Degenen die een gemeenschappelijk hoekpunt hebben.

In een vierhoek zijn ze aangrenzende hoeken Degenen die een kant delen, terwijl tegenover de hoeken Ze hebben geen gemeenschappelijke kanten. Een ander belangrijk kenmerk van een vierhoek is dat de som van zijn vier Interne hoeken Het is twee keer de vlakke hoek, dat is 360º of 2π radialen.

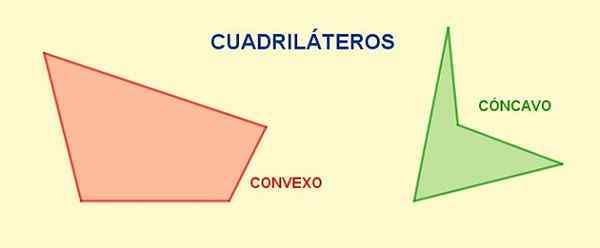
Figuur 1. Verschillende vierhoek. Bron: f. Zapata.

De diagonalen Het zijn de segmenten die een hoekpunt verenigen met het tegenovergestelde en in een bepaalde ring, uit elk hoekpunt kunt u een enkele diagonaal tekenen. Het totale aantal diagonalen van een vierhoek is twee.

Vierhuizen zijn figuren die sinds de oude tijden bekend zijn bij de mensheid. Archeologische gegevens, evenals de constructies die vandaag overleven, bevestigen.

Ook vandaag blijven de vierhoekige quadrilateralen een belangrijke aanwezigheid hebben in het dagelijkse leven van iedereen. De lezer kan dit formulier op het scherm vinden waarop de tekst op dit precieze moment leest, in de vensters, de deuren, de auto -onderdelen en talloze plaatsen meer.

[TOC]

Classificatie van vierhoekig

Volgens de parallellisme van de tegenoverliggende zijden zijn de vierhoekig geclassificeerd als volgt:

1. Trapezoid, Als er geen parallellisme is en de vierhoek is convex.
2. Trapeze, Wanneer er parallellisme is tussen een enkel paar tegenovergestelde kanten.
3. Parallellogram, Wanneer hun tegenovergestelde kanten parallel zijn twee tot twee.

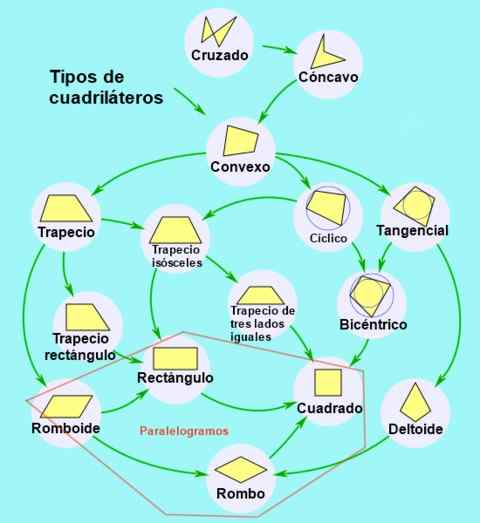Figuur 2. Classificatie en subclassificatie van vierhoekig. Bron: Wikimedia Commons.

Soorten parallellogram

Op hun beurt kunnen parallellogrammen als volgt worden geclassificeerd volgens hun hoeken en partijen:

1. Rechthoek, Het is het parallellogram dat zijn vier interne hoeken van gelijke mate heeft. De interne hoeken van een rechthoek vormen een rechte hoek (90º).
2. Vierkant, Het is een rechthoek met zijn vier zijden van gelijke mate.
3. Diamant, Het is het parallellogram met zijn vier zijden, maar zijn verschillende aangrenzende hoeken.
4. Rhomboid, Parallellogram met verschillende aangrenzende hoeken.

Trapeze

De trapeze is een convex vierhoek met twee parallelle zijden.

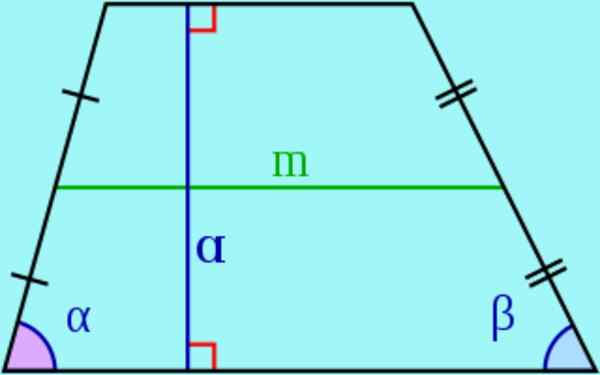figuur 3. Bases, laterale, hoogte en mediaan van een trapeze. Bron: Wikimedia Commons.

- In een trapeze worden de parallelle zijden genoemd honken En de niet -parallellen worden genoemd zijdelings.

- De hoogte van een trapeze is de afstand tussen de twee basen, dat wil zeggen de lengte van een segment met uiteinden in de basen en loodrecht op hetzelfde. Dit segment wordt ook een trapezehoogte genoemd.

- De mediaan Het is het segment dat de middelpunten van de zijkanten verbindt. Het kan worden aangetoond dat de mediaan parallel is aan de bases van de trapeze en de lengte ervan is gelijk aan de semi -knooppunten van de bases.

- Het gebied van een trapeze is zijn hoogte vermenigvuldigd met de semi -body's van de bases:

Oppervlakte van een trapeze = hoogte * (basis 1 + basis 2) / 2

Soorten trapeze

-Rechthoek trapeze: Het is degene die een kant heeft loodrecht op de bases. Deze kant is ook de hoogte van de trapezoid.

-Trapezium eisosceles: Degene met gelijke lengte zijden. In een gelijkbenige trapezoid zijn de hoeken naast de basen gelijk.

-Escaleno trapezio: Degene die zijn zijkanten van verschillende lengte heeft. De tegengestelde hoeken kunnen acuut zijn en de andere stompe, maar het kan ook gebeuren dat beide stompe of beide acuut zijn.

Kan u van dienst zijn: opgeloste factorisatieoefeningen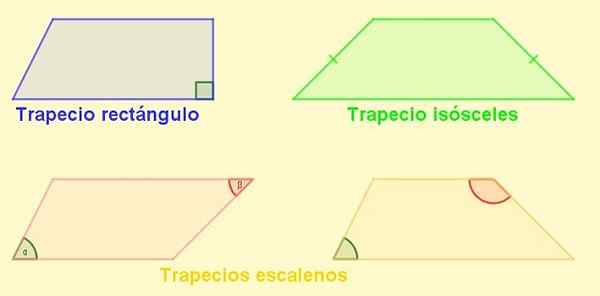 Figuur 4. Soorten trapeze. Bron: f. Zapata.

Parallellogram

Het parallellogram is een vierhoek wiens tegenovergestelde zijden parallel zijn twee tot twee. In een parallellogram zijn de tegenovergestelde hoeken hetzelfde en zijn de aangrenzende hoeken aanvullend, of met andere woorden, de aangrenzende hoeken in totaal 180º.

Als een parallellogram een ​​rechte hoek heeft, dan zullen alle andere hoeken ook zijn en wordt de resulterende figuur genoemd rechthoek. Maar als de rechthoek ook zijn aangrenzende zijden van dezelfde lengte heeft, dan zijn alle zijden gelijk en is de resulterende figuur een vierkant.

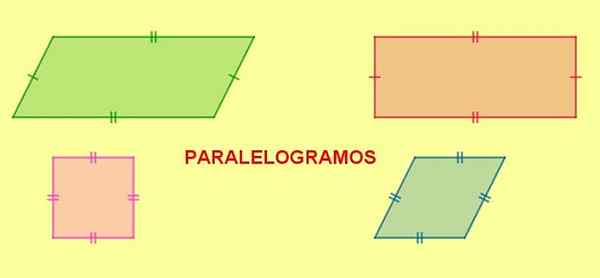Figuur 5. Parallellogrammen. De rechthoek, het vierkant en de rhombus zijn parallellogrammen. Bron: f. Zapata.

Wanneer een parallellogram twee aangrenzende zijden van dezelfde lengte heeft, zullen alle zijden van dezelfde lengte zijn en de resulterende figuur is een diamant.

De hoogte van een parallellogram is een segment met uiteinden aan de tegenovergestelde zijden en loodrecht op hen.

Een parallellogramgebied

Het gebied van een parallellogram is het product van de basis op zijn hoogte, de basis is een zij loodrecht op de hoogte (figuur 6).

Oppervlakte van een parallellogram = basis x hoogte = a . H

Diagonalen van een parallellogram

Het kwadraat van de diagonaal dat begint bij een hoekpunt is gelijk aan de som van de vierkanten van de twee zijden grenzend aan het genoemde hoekpunt meer het dubbele product van die zijden door de cosinus van de hoek van die hoekpunt:

F² = A² +  D² + 2 a d cos (α)

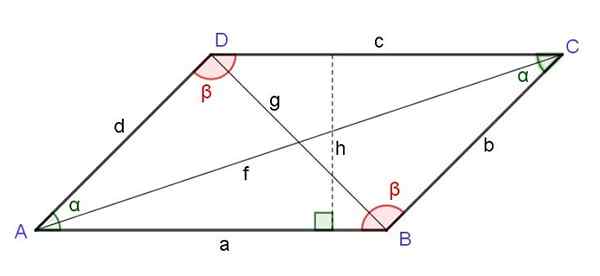Figuur 6. Parallellogram. Tegenover de hoeken, hoogte, diagonalen. Bron: f. Zapata.

Het kwadraat van de diagonale tegen het hoekpunt van een parallellogram is gelijk aan de som van de vierkanten van de twee zijden grenzend aan deze hoekpunt en heeft het dubbele product van die zijkanten afgetrokken door de cosinus van de hoek van dat hoekpunt:

G² = A² + D² - 2 a d cos (α)

Parallellogrammen wet

In elk parallellogram is de som van de vierkanten van hun zijden gelijk aan de som van de vierkanten van de diagonalen:

naar² + B² + C² + D² = f² + G²

Met betrekking totctangle

De rechthoek is een vierhoek met zijn tegenovergestelde zijden parallel twee tot twee en dat heeft ook een rechte hoek. Dat wil zeggen dat de rechthoek een soort parallellogram is met een rechte hoek. Voor het parallellogram, De rechthoek heeft de tegenovergestelde zijden van gelijke lengte A = C en B = D. 

Maar zoals in elk parallellogram aangrenzende hoeken zijn aanvullend en de gelijke tegenovergestelde hoeken, in de rechthoek door een rechte hoek te hebben, zal het noodzakelijkerwijs rechte hoeken vormen in de andere drie hoeken. Het is te zeggen In een rechthoek meet alle interne hoeken 90º of π/2 radialen.

Diagonalen van een rechthoek

In een rechthoek zijn de diagonalen gelijke lengte, Zoals hieronder zal worden aangetoond. De redenering is als volgt; Een rechthoek is een parallellogram met al zijn rechte hoeken en daarom erft het alle eigenschappen van het parallellogram, inclusief de formule die de lengte van de diagonalen geeft:

F² = A²+  D² + 2 a d cos (α)

G² = A² + D² - 2 a d cos (α)

met α = 90º

Als Cos (90º) = 0, Dus het gebeurt dat:

F² = g² = A² +  D²

Dat is f = g, en daarom de lengtes F En G Van de twee diagonalen van de rechthoek zijn ze gelijk en hun lengte wordt gegeven door:

Diagonale lengte van een rechthoek = √ (a² + B²))

Bovendien, indien in een rechthoek van aangrenzende kanten naar En B De ene zijde is gebaseerd op de andere kant, zal hoogte zijn en bijgevolg zal het rechthoekige gebied zijn:

Het kan u van dienst zijn: Fibonacci -serie: eigenschappen, natuurlijke relaties, toepassingen

Rechthoekgebied = A x B.

De perimeter is de som van alle zijden van de rechthoek, maar omdat de tegenstellingen hetzelfde zijn, is het dan nodig voor een zijde rechthoek naar En B De perimeter wordt gegeven door de volgende formule:

Rechthoek perimeter = 2 (a + b)

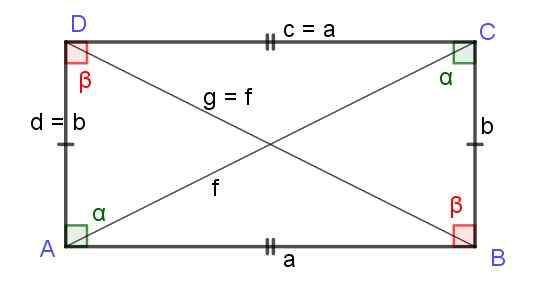Figuur 7. Rechthoek van zijkanten a en b. De diagonalen f en g zijn gelijke lengte. Bron: f. Zapata.

Vierkant

Het vierkant is een rechthoek met zijn aangrenzende zijden van dezelfde lengte. Als het plein kant heeft naar, Dan zijn diagonalen F En G Ze hebben dezelfde lengte, dat is F = g = (√2) a.

Het gebied van een vierkant is de zijde verheven tot het vierkant:

Oppervlakte van een vierkant = a²

De omtrek van een vierkant is twee keer de zijkant:

Perimeter van een vierkant = 4 a

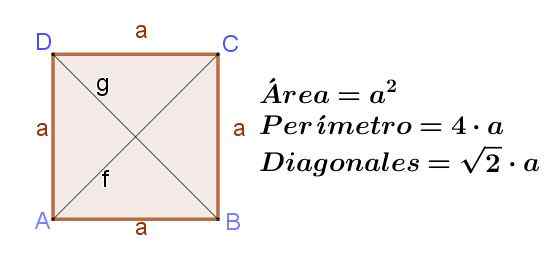Figuur 8. Vierkant naar zij A, die het gebied, zijn omtrek en de lengte van zijn diagonalen aangeeft. Bron: f. Zapata ..

Diamant

De rhombus is een parallellogram met zijn aangrenzende zijden van dezelfde lengte, maar zoals in een parallellogram zijn de tegenoverliggende zijden dan hetzelfde, Alle zijden van een rhombus zijn gelijke lengte.

De diagonalen van een rhombus zijn van verschillende lengte, maar ze worden onder rechtse hoeken gesneden.

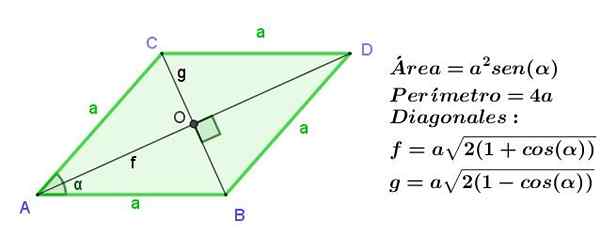Figuur 9. Rhombus van zijde A, die het gebied, perimeter en de lengte van zijn diagonalen aangeeft. Bron: f. Zapata.

Voorbeelden

voorbeeld 1

Toon aan dat in een vierhoek (niet gekruist) de interne hoeken in totaal 360º.

Figuur 10: Het wordt aangetoond als de som van de hoeken van een vierhoekig toevoegen 360º. Bron: f. Zapata.

ABCD wordt beschouwd als een ABCD (zie figuur 10) en de diagonale BD is getekend. Er worden twee ABD- en BCD -driehoeken gevormd. De som van de interne hoeken van de ABD -driehoek is:

α + β₁ + δ₁ = 180º

En de som van de interne hoeken van de BCD -driehoek is:

 β2 + γ + δ₂ = 180º

Het toevoegen van de twee vergelijkingen wordt verkregen:

α + β₁ + δ₁ +  β₂ + γ + δ₂ = 180º + 180º

Groepering:

α + (β₁ +  β₂) + (δ₁ + δ₂) + γ = 2* 180º

Groepering en renoveren wordt eindelijk aangetoond dat:

α + β + δ + γ = 360º

Voorbeeld 2

Toon aan dat de mediaan van een trapezium parallel is aan zijn bases en de lengte is het semi -seismum van de bases.

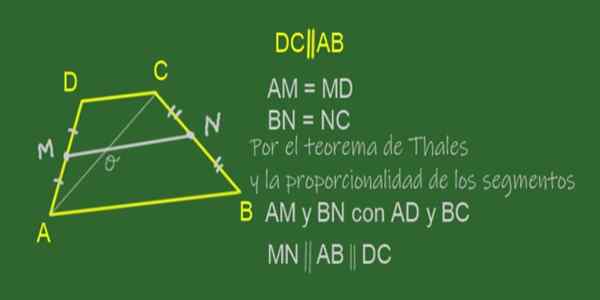Figuur 11. Mediane MN van de ABCD -trapeze. Bron: f. Zapata.

De mediaan van een trapeze is het segment dat de middelpunten van zijn zijkanten verbindt, dat wil zeggen de niet -parallelle zijden. In de ABCD -trapeze getoond in figuur 11 is de mediaan Mn. 

Omdat het een middelpunt is van AD- en N Mid -BC -punt, is het vervuld dat quotiënten AM / AD en BN / BC gelijk zijn.

Dat wil zeggen, AM is evenredig met BN in dezelfde verhouding als AD is BC, dus de voorwaarden voor de toepassing van de stelling (wederzijds) van Thales die het volgende bevestigen:

"Indien in drie of meer rechte snit door twee Secant".

In ons geval wordt geconcludeerd dat de MN-, AB- en DC -lijnen daarom parallel aan elkaar zijn:

"LIn een mediaan is een van een trapeze parallel aan zijn bases".

Kan u van dienst zijn: gecombineerde bewerkingen

Nu zal de stelling van Thales van toepassing zijn:

"Een set parallellen gesneden door twee of meer drogen bepalen proportionele segmenten".

In ons geval AD = 2 AM, AC = 2 AO, dus de DAC -driehoek is vergelijkbaar met de MAO -driehoek, en bijgevolg DC = 2 Mo.

Een soortgelijk argument maakt het mogelijk te bevestigen dat Cu vergelijkbaar is met Con, waarbij Ca = 2 Co en Cb = 2 CN. Hieruit volgt dat AB = 2 op.

Kortom, ab = 2 op y 2 mo. Dus als we zijn vertrokken:

Ab + dc = 2 op + 2 mo = 2 (mo + aan) = 2 mn

Eindelijk wist Mn:

Mn = (AB + DC) /2

En er wordt geconcludeerd dat de mediaan van een trapezium de semi -knooppunten van de basen meet, of met andere woorden: de mediaan meet de som van de basen, gedeeld door twee.

Voorbeeld 3

Toon aan dat in een rhombus de diagonalen onder rechtse hoeken worden gesneden.

Figuur 12. Rhombus en demonstratie dat hun diagonalen in rechtse hoeken worden gesneden. Bron: f. Zapata.

Het bestuur van figuur 12 toont de nodige constructie. Eerst wordt het ABCD -parallellogram getekend met AB = BC, dat is een rhombus. De AC- en DB -diagonalen bepalen acht hoeken die in de figuur worden getoond.

Met behulp van de stelling (a.Je.P.) Dat stelt dat interne alternatieve hoeken tussen parallellen gesneden door een Secant Gelijke hoeken bepalen, we kunnen het volgende vaststellen:

α₁ = γ₁, α2 = γ2, δ₁ = Β₁ en Δ2 = β2. (*)

Aan de andere kant, aangezien de aangrenzende zijden van een rhombus van gelijke lengte zijn, worden vier gelijkbenige driehoeken bepaald:

DAB, BCD, CDA en ABC

Nu wordt de driehoeken (gelijkbenig) ingeroepen die stelt dat de hoeken naast de basis van gelijke mate zijn, waar wordt geconcludeerd dat:

δ₁ = β2, Δ2 = β₁, α2 = γ₁ en α₁ = γ2 (**)

Als relaties (*) en (**) worden gecombineerd, wordt de volgende gelijkheid van hoeken bereikt:

α₁ = α2 = γ₁ = γ₁ Aan de ene kant en β₁ = Β2 = δ₁ = Δ2 voor de andere. 

Herinnering aan de stelling van de gelijke driehoeken die bevestigt dat twee driehoeken met een gelijke zijde tussen twee gelijke hoeken hetzelfde zijn, zijn:

Aod = aoB en bijgevolg ook de hoeken ∡aod = ∡aob.

Dan ∡aod + ∡aob = 180º, maar omdat beide hoeken van gelijke mate zijn, 2 ∡aod = 180º wat impliceert dat ∡aod = 90º.

Dat wil zeggen, het wordt geometrisch aangetoond dat de diagonalen van een rhombus op rechtse hoeken worden gesneden.

Oefeningen opgelost

- Oefening 1

Toon aan dat niet-EG-hoeken in een rechthoekige trapezoid aanvullend zijn.

Oplossing

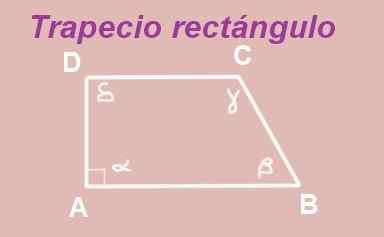Figuur 13. Rechthoek trapeze. Bron: f. Zapata.

ABCD Trapezoid is gebouwd met parallelle AB- en DC -bases. De binnenste hoek van hoekpunt A is recht (meet 90º), dus je hebt een rechthoekige trapezoid.

De hoeken α en A zijn interne hoeken tussen twee parallelle AB- en DC -parallellen, daarom zijn ze hetzelfde, dat wil zeggen Δ = α = 90º. 

Aan de andere kant is aangetoond dat de som van de interne hoeken van een vierhoek 360º toevoegt, dat wil zeggen:

α + β + γ + Δ = 90º + β + 90º + δ = 360º.

Het bovenstaande leidt naar:

 β + Δ = 180º

Bevestigend wat wilde worden aangetoond dat de hoeken β en δ aanvullend zijn.

- Oefening 2

Een ABCD -parallellogram heeft AB = 2 cm en AD = 1 cm, bovendien is de hoek slecht 30º. Bepaal het gebied van genoemde parallellogram en de lengte van zijn twee diagonalen.

Oplossing

Het gebied van een parallellogram is het product van de lengte van de basis op hoogte. In dit geval wordt de lengte van het segment B = AB = 2 cm als een basis genomen, de andere zijde heeft lengte A = AD = 1 cm en de hoogte H zal als volgt worden berekend:

H = ad * sin (30º) = 1 cm * (1/2) = ½ cm.

Dan: gebied = b * h = 2 cm * ½ cm = 1 cm².

Referenties

1. C. EN. NAAR. (2003). Geometrie -elementen: met oefeningen en kompasgeometrie. Universiteit van Medellin.
2. Campos, f., Cerecedo, f. J. (2014). Wiskunde 2. Patria -redactiegroep.
3. Vrijgelaten, k. (2007). Ontdek polygonen. Benchmark -onderwijsbedrijf.
4. Hendrik, V. (2013). Gegeneraliseerde polygonen. Birkhäuser.
5. Iger. (S.F.)). Wiskunde eerste semester Tacaná. Iger.
6. Jr. Geometrie. (2014). Polygonen. Lulu Press, Inc.
7. Miller, Heeren, & Hornsby. (2006). Wiskunde: redeneren en applicaties (tiende editie). Pearson Education.
8. Patiño, m. (2006). Wiskunde 5. Redactionele progreso.
9. Wikipedia. Vierhoek. Hersteld van: is.Wikipedia.com