Boltzmann constante geschiedenis, vergelijkingen, berekening, oefeningen

De Boltzmann constant Het is de waarde die de gemiddelde kinetische energie van een thermodynamisch systeem of een object met de absolute temperatuur van hetzelfde relateert. Hoewel ze vaak in de war zijn, zijn temperatuur en energie niet hetzelfde concept.

De temperatuur is een maat voor energie, maar niet de energie zelf. Met de Boltzmann -constante is de ene als volgt aan elkaar gekoppeld:

EN_C = (3/2) k_B  T

Boltzmann -gastheer in Wenen. Bron: Dadotet bij Engelse Wikipedia [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/]]

Deze vergelijking is geldig voor een ideaal monoatomisch gasmolecuul M, waar EN_C Het is zijn kinetische energie gegeven in Joules, k_B Het is de constante van Boltzmann en T Het is de absolute temperatuur in Kelvin.

Op deze manier, wanneer de temperatuur stijgt, neemt ook de gemiddelde kinetische energie per stofmolecuul toe, zoals verwacht zal plaatsvinden. En het tegenovergestelde gebeurt wanneer de temperatuur daalt, het kunnen bereiken van het punt waar de hele beweging stopt, de laagst mogelijke of absolute temperatuur wordt bereikt.

Bij het praten over gemiddelde kinetische energie is het noodzakelijk om te onthouden dat kinetische energie wordt geassocieerd met beweging. En de deeltjes kunnen op veel manieren bewegen, bijvoorbeeld bewegen, roteren of trillen. Natuurlijk zal niet iedereen het op dezelfde manier doen, en omdat ze talloze zijn, wordt het gemiddelde genomen om het systeem te karakteriseren.

Sommige energietoestanden zijn waarschijnlijker dan andere. Dit concept is van radicaal belang in de thermodynamica. De energie die in de vorige vergelijking wordt beschouwd, is kinetische vertalingsenergie. Van de waarschijnlijkheid van de staten en hun relatie met de Boltzmann -constante zullen iets later praten.

In 2018 werd de Kelvin opnieuw gedefinieerd en met hem de Boltzmann -constante, die in het internationale systeem ongeveer 1 is.380649 x 10^-23 J. K^-1. Veel meer precisie kan worden bereikt voor de Boltzmann Constante, die in talloze laboratoria over de hele wereld is bepaald, met verschillende methoden.

[TOC]

Geschiedenis

De beroemde constante is zijn naam te danken aan de fysicus Ludwig Boltzmann (1844-1906), geboren in Wenen, die zijn leven als wetenschapper wijdde aan de studie van het statistische gedrag van de systemen met veel deeltjes, vanuit het oogpunt van Newtoniaanse mechanica.

Hoewel het bestaan ​​van het atoom tegenwoordig universeel wordt geaccepteerd, was in de negentiende eeuw het geloof over de vraag of het atoom echt bestond of een artifice was waarmee veel fysieke fenomenen werden uitgelegd, in het volledige debat.

Kan u van dienst zijn: normale vector: berekening en voorbeeld

Boltzmann was een sterke verdediger van het bestaan ​​van het atoom, en in zijn tijd stond hij voor harde kritiek op zijn werk door veel collega's, die van mening waren dat ze onoplosbare paradoxen bevatten.

Hij verklaarde dat waarneembare fenomenen op macroscopische niveaus konden worden verklaard door de statistische eigenschappen van samenstellende deeltjes zoals atomen en moleculen.

Deze kritiek kan te wijten zijn aan de diepe aflevering van depressie die hem ertoe bracht zijn eigen leven te nemen begin september 1906, toen hij nog veel te doen had, omdat hij werd beschouwd als een van de grote theoretische fysici van zijn tijd en daar was weinig aan dat andere wetenschappers zullen bijdragen aan het bevestigen van de waarheidsgetrouwheid van hun theorieën.

Het gebeurde niet lang na zijn dood toen nieuwe ontdekkingen over de aard van het atoom en zijn samenstellende deeltjes zouden worden toegevoegd om de reden te geven aan Boltzmann.

Boltzmann's Constant en Planck's Works

Nu, de constante van Boltzmann k_B Het werd geïntroduceerd zoals het vandaag bekend is, een tijdje na het werk van de Oostenrijkse natuurkundige. Het was Max Planck, in zijn wet van de emissie van het zwarte lichaam, een werk dat hij in 1901 presenteerde, die hem op dat moment de waarde van 1,34 x 10 gaf²³ J/K.

Tegen het jaar 1933 werd Boltzmann aan Wenen toegevoegd als een poster eerbetoon aan een plaque met de definitie van entropie waarbij de beroemde constante betrokken was: S = K_B Log W, vergelijking die later zal worden besproken.

Tegenwoordig is de constante van Boltzmann onmetelijk bij de toepassing van de thermodynamische wetten, statistische mechanica en informatietheorie, waarvan deze fysicus met een triest einde een pionier was.

Waarde en vergelijkingen

Gassen kunnen worden beschreven in macroscopische termen en ook in microscopische termen. Voor de eerste beschrijving zijn er concepten zoals dichtheid, temperatuur en druk.

Er moet echter aan worden herinnerd dat een gas bestaat uit veel deeltjes, die een globale neiging hebben tot een bepaald gedrag. Het is die trend die macroscopisch wordt gemeten. Een manier om de constante van Boltzmann te bepalen, is dankzij de goed bekende vergelijking van ideale gassen:

P.V = n. R. T

Hier P Het is gasdruk, V Het is het volume, N Het is het aantal aanwezige mol, R Het is de constante van de gassen en T Het is de temperatuur. In een mol ideaal gas wordt de volgende relatie tussen het product vervuld P.V, en de kinetische energie van vertaling K De hele set is:

Kan u van dienst zijn: corpusculair model van materie

P.V = (2/3). K

Daarom is kinetische energie:

K = (3/2) n.R.T

Door te delen door het totale aantal aanwezige moleculen, dat N wordt genoemd, wordt de gemiddelde kinetische energie van een enkel deeltje verkregen:

EN_C = K /n

EN_C= (3/2n) n.R.T

In een mol is er het aantal deeltjes n_NAAR, En daarom is het totale aantal deeltjes N = nnA, verblijf:

EN_C = (3/2nn_NAAR) N.R.T

Precies het quotiënt R/n_NAAR Het is de constante van Boltzmann, aangetoond dat de kinetische energie van de gemiddelde translatie van een deeltje alleen afhangt van de absolute temperatuur en niet andere grootten zoals druk, volume of zelfs het type molecuul:

EN_C = (3/2) k_B. T

Boltzmann's constante en entropie

Een gas heeft een gegeven temperatuur, maar die temperatuur kan overeenkomen met verschillende interne energietoestanden. Hoe dit verschil te visualiseren?

Overweeg de gelijktijdige lancering van 4 munten en de manieren waarop ze kunnen vallen:

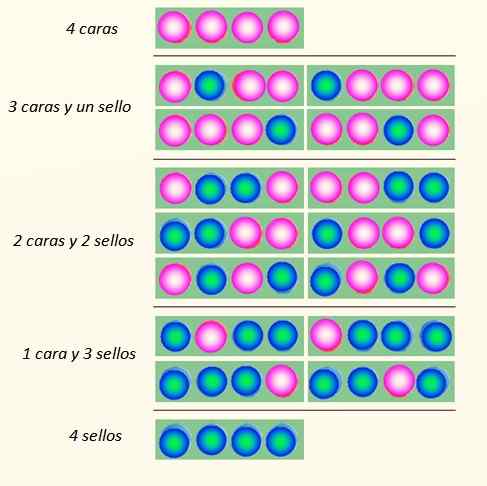Manieren waarop 4 munten kunnen vallen. Bron: zelf gemaakt

De muntenset kan in totaal 5 staten aannemen, die worden overwogen Macroscopisch, beschreven in de figuur. Welke van deze staten zou de lezer zeggen dat dit het meest waarschijnlijk is?

Het antwoord moet de staat van 2 gezichten en 2 kruisen zijn, omdat het in totaal 6 mogelijkheden heeft, van de 16 geïllustreerde in de figuur. En 2⁴ = 16. Deze zijn gelijk aan de staten microscopisch.

En wat als 20 munten worden gelanceerd in plaats van 4? Er zouden in totaal 2 zijn^twintig mogelijkheden of "microscopische toestanden". Het is een veel groter en moeilijker aantal om te hanteren. Om het beheer van grote aantallen te vergemakkelijken, zijn logaritmen zeer geschikt.

Nu lijkt het duidelijk dat de staat met de grootste stoornis het meest waarschijnlijk is. De meest geordende staten zoals 4 gezichten of 4 postzegels zijn iets minder waarschijnlijk.

De entropie van een macroscopische toestand wordt gedefinieerd als:

S = K_B ln w

Waar W Het is het aantal mogelijke microscopische toestanden en k_B Het is de constante van Boltzmann. Als ln w Het is dimensieloze, entropie heeft dezelfde eenheden als k_B: Joule/K.

Dit is de beroemde vergelijking in de grafsteen van Boltzmann in Wenen. Meer dan entropie is de relevante echter de verandering ervan:

Het kan u van dienst zijn: thermodynamische variabelen: welke zijn en oefeningen opgelost

Δs = k_B ln w₂ - k_B ln w₁ = K_B ln (w₂/W₁))

Hoe wordt K berekend_B?

De waarde van de Boltzmann -constante wordt experimenteel precies verkregen met metingen op basis van akoestische thermometrie, die worden uitgevoerd met behulp van de eigenschap die de afhankelijkheid van de snelheid van geluid in een gas met de temperatuur van hetzelfde vaststelt.

Inderdaad, de snelheid van het geluid in een gas wordt gegeven door:

Waar B _adiabatisch Het is de adiabatische samendrukbaarheidsmodule gegeven door:

B_adiabatisch = γp

En ρ is gasdichtheid. Voor de vorige vergelijking, P Het is de druk van het gas in kwestie en γ Het is de adiabatische coëfficiënt, waarvan de waarde voor een specifiek gas wordt gevonden in tabellen.

Metrologie -instituten ervaren ook andere manieren om de constante te meten, zoals Johnson Noise thermometrie, die de thermische schommelingen gebruikt die willekeurig in de materialen voorkomen, met name in bestuurders.

Opgeloste oefeningen

-Oefening 1

Vinden:

a) De kinetische energie van gemiddelde vertaling EN_C die een ideaal gasmolecuul heeft bij 25 ºC

b) De kinetische energie van vertaling K van de moleculen in 1 mol van dit gas

c) De gemiddelde snelheid van een zuurstofmolecuul bij 25 ºC

Feit

M_zuurstof = 16 x 10 ^-3 kg/mol

Oplossing

naar) EN_C = (3/2) k t = 1.5 x 1.380649 x 10^-23J. K^-1 x 298 k = 6.2 x 10^{-eenentwintig} J

B) K = (3/2) n.R.T = 5 x 1 mol x 8.314 J/Mol .K x 298 K = 3716 J

C) EN_C = ½ mV², Rekening houdend met dat het zuurstofmolecuul diatomeeën is en de molaire massa moet worden vermenigvuldigd met 2, zal het zijn:

-Oefening 2

Vind de verandering van entropie wanneer 1 mol gas bezet met een volume van 0.5m³ Het breidt zich uit om 1 m te bezetten³.

Oplossing

Δs = k_B ln (w₂/W₁))

W₂= 2^NW₁ (Er waren 2⁴ Microscopische toestanden voor de lancering van de 4 munten, onthoud?))

Waarbij n het aantal deeltjes is dat aanwezig is in 0.5 mol gas 0.5 x n_NAAR:

Δs = k_B ln (2^N W₁/W₁) = K_B LN 2^N= K_B 0.5n_NAAR ln 2 = 2.88 J/K

Referenties

1. Atkins, P. 199999. Fysische chemie. Omega -edities. 13-47.
2. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill. 664-672.
3. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e ... Ed Prentice Hall. 443 -444.
4. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. 647-673.
5. Als herdefinitie. Kelvin: Boltzmann Constant. Hersteld van: nist.Gov