Behoud van het lineaire momentia -principe, voorbeelden, oefeningen.

De Behoud van lineair momentum van een lichaam stelt vast dat het product van zijn massa door zijn snelheidsvector een constante hoeveelheid is, wanneer het lichaam vrij is van interactie met andere lichamen en met de snelheid gemeten ten opzichte van een vast of niet-acuut referentiesysteem.

Als er verschillende lichamen zijn die alleen tussen hen op elkaar inwerken, maar niet met de externe omgeving, dan is de lineair momentum van de set blijft ook in de loop van de tijd constant.

Een astronaut in de ruimte is vrij van alle interactie, dus het lineaire moment

Het lineaire moment, de hoeveelheid lineaire beweging of gewoon de momentum, Het wordt aangeduid met de brief P En het is een vectorbedrag:

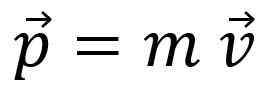
Het lineaire moment is niet hetzelfde als de snelheid, hoewel de verhouding duidelijk is: een vrachtwagen die tot 20 km/u gaat, heeft meer lineaire tijd dan een fiets die op dezelfde snelheid beweegt.

Om het lineaire moment van een lichaam te veranderen, is het noodzakelijk dat een netto externe kracht erop werkt, anders blijft deze constant. Bovendien het lineaire moment P van een systeem gevormd door N-lichaam Het is de vector som van individuele momenten:

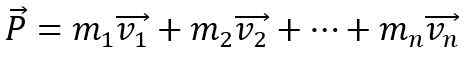
[TOC]

Principe van behoud van de hoeveelheid lineaire beweging

In een lichaam vrij van krachten (of een waarin alle krachten erop worden geannuleerd) gebeurt het dat het lineaire moment.

Op dezelfde manier passeert het in een systeem gevormd door verschillende lichamen die alleen met elkaar communiceren, maar niet met de buitenste omgeving: het totale lineaire moment van het systeem blijft gefixeerd tijdens de evolutie van de set van de set.

Dit behoudsprincipe wordt als volgt vermeld:

Het totale lineaire moment van een set N-body dat alleen met elkaar interageert, maar niet met de externe omgeving, is een onveranderlijke hoeveelheid op tijd.

En wiskundig wordt het als volgt uitgedrukt:

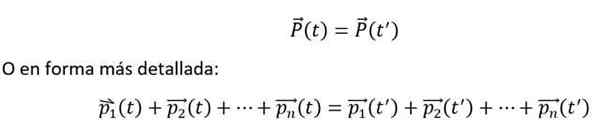
De vorige gelijkheid wordt vervuld, als en alleen als de N-Lichamen werken met elkaar in, maar niet met de externe omgeving. Bovendien moeten individuele momenten altijd worden gemeten met betrekking tot een traagheidsreferentiesysteem.

Voorbeelden

voorbeeld 1

Twee astronauten in de ruimte worden uit de handen gehaald en blijven in een vaste positie ten opzichte van het schip. Maar ze duwen elkaar wel, ze beginnen in tegengestelde richtingen te scheiden, wanneer ze vanuit het schip worden gezien.

Het kan u van dienst zijn: theorie van de oerknal: kenmerken, fasen, bewijs, problemen

In dit geval, aangezien de interactie tussen astronauten slechts onder hen is door de contactkracht van hun handen, het totale lineaire moment. Dat wil zeggen, totale lineaire tijd 0.

Het lineaire moment van elke astronaut is echter veranderd. Aanvankelijk had elk een lineair moment 0 ten opzichte van het schip, maar nadat het de ene duwt in de ene richting en de andere in de tegenovergestelde richting komt, met niet-nul lineaire momenten van gelijke grootte en tegengestelde adressen.

Dus wanneer de individuele momenten vectoraal worden toegevoegd, wordt het initiële totale lineaire momentum daardoor verkregen, wat nietig is.

Aan de andere kant, het behoud van het lineaire moment van het bedrag. Maar het resultaat van het vermenigvuldigen van zijn massa met zijn snelheid is gelijk aan het product verkregen door de massa van de ander te vermenigvuldigen met de snelheid van de ander.

Voorbeeld 2

Een puppy bevindt zich op een drijvend platform in een meer van rustig water en de eigenaar ziet het vanuit een dok. In het begin zijn zowel het platform als de puppy in rust, maar wanneer de puppy de eigenaar wil benaderen, gaat het platform weg van het dok.

De verklaring voor deze observatie is precies in het principe van behoud van het lineaire momentumbedrag. Het systeem bestaat uit de puppy en het platform.

De puppy kan op het platform lopen dankzij de wrijvingskracht tussen zijn benen en het oppervlak, in dit geval is de wrijvingskracht een interne interactie tussen het en het platform.

De set is een geïsoleerd systeem en het platform kan horizontaal op het meer bewegen, vrij van alle bewegingsweerstand. Aan de andere kant, in verticale richting, zijn alle krachten in balans en gecompenseerd, en de set heeft geen beweging in die richting.

Daarom worden in deze situatie aan alle hypothesen voldaan, zodat het principe van behoud van het lineaire momentum wordt toegepast.

Voorbeeld 3

Een eskimo zit gevangen in het midden van een ijs, het ijs is zo soepel dat het niet uitmaakt hoeveel geprobeerd is, de Eskimo glijdt en blijft altijd op dezelfde plaats.

De enige mogelijke manier waarop de Eskimo het meer verlaat, is dat het in de richting ligt tegengesteld aan welke een zwaar object dat in zijn rugzak draagt ​​(ervan uitgaande).

Kan u van dienst zijn: Geometrische optiek: welke studies, wetten, toepassingen, oefeningen

Toepassingen

Verzend in de ruimte

Het behoud van het lineaire moment. In dit geval wordt de impuls van het schip bereikt door uitwijzing van gassen met hoge snelheid, zodat de raket in de tegenovergestelde richting kan bewegen waarnaar ze zijn uitgezet.

Als het schip oorspronkelijk in rust is, wanneer de brandstof wordt verbrand en uitgezet, treedt de uitwijzingskracht op tegen het schip zelf. Het is een interne kracht tussen gassen en het schip. Er zijn geen externe krachten en brengt daarom het behoud van het lineaire moment toe.

Aangezien het lineaire moment van gassen hetzelfde is en in tegenstelling tot dat van het schip, slaagt het erin om rust te verlaten en verhoogt het door gassen te verdrijven, de hoeveelheid beweging en dus zijn snelheid.

Dagelijks leven

Een ander geval voor het behoud van het lineaire moment.

Men zou kunnen stellen dat het principe in dit geval niet van toepassing is, omdat er een externe kracht is: de weerstand die het hout aan de kruidnagel heeft aangeboden.

Op het moment van contact is de kracht die de hamer afdrukt tot de nagel een interne kracht (tussen het systeem dat de nagel en de hamer is) veel groter dan de weerstand waar het hout tegen is, en daarom is deze laatste te verwaarlozen.

Het hele lineaire moment van de hamer, die vrij groot is vanwege de grote massa en snelheid, wordt net na de botsing op de nagel overgebracht. Merk op dat het hele moment wordt overgebracht, maar niet alle kinetische energie van de hamer, omdat een deel ervan wordt omgezet in thermische energie in de nagel en de hamer, die zijn temperatuur na de impact verhoogt.

Opdrachten

Oefening 1

Andrew en Berenice astronauten zijn uit het ruimtestation dat uit beide handen en in rust is genomen ten opzichte van het station. Ze rijden duwen hun handen tegen die van de ander en ze worden vrijgelaten. Als Andrew, 70 kg massa beweegt op 1 m/s ten opzichte van het station, wat is de snelheid van Berenice met 49 kg massa?

Oplossing

In dit geval wordt de hypothese van het behoud van het lineaire momentum duidelijk toegepast, omdat er geen externe krachten in externe ruimte zijn. De kracht waarmee hun handen beide astronauten duwen, is een interne kracht.

Het kan u van dienst zijn: WAVE DIFFRAFTIE: Concept en voorbeelden

Stel dat Andrew's mis is_naar en dat van Berenice M_B. Evenzo zijn de snelheden van beide na de impuls V_naar Voor Andrew en V_B Voor Berenice. Dan wordt het behoud van het lineaire momentum als volgt toegepast:

M_naar∙0 + M_B∙0 = M_naar∙V_naar+ M_B∙V_B

De snelheid van Berenice opruimen die je hebt:

V_B = - (m_naar / M_B) ∙ V_naar

Numerieke waarden plaatsen:

V_B = - (70/49) ∙ (1m / s) of = -1,43 m/s of

Dat wil zeggen dat Berenice snel 1,43 m/s in de tegenovergestelde richting van Andrew beweegt.

Oefening 2

Een puppy loopt naar de eigenaar op de top van een semi-gevestigd platform. Bron: f. Zapata.

Een deeg van 5 kg bevindt zich in rust op een platform van 15 kg dat, ook in rust, op een stille meer zweeft. Als de puppy hiermee met een snelheid van 0,5 m/s op het platform begint te lopen. Hoe snel zullen de puppy en het platform met betrekking tot een vaste waarnemer om te gaan?

Oplossing

Het zal worden genomen als een traagheidsreferentiesysteem naar het dok waar de puppy -eigenaar is. Aanvankelijk zijn zowel de puppy als het drijvende platform in rust ten opzichte van het dok.

Wanneer de puppy besluit snel naar de eigenaar te lopen V ' Wat betreft het platform, dan beweegt het platform weg van de veer met snelheid +V. De snelheid van de puppy ten opzichte van het dok wordt bereikt door de vectorsom van zijn snelheid ten opzichte van het platform plus de snelheid van het platform en geeft het aan door:

v = -v' + V

Aangezien de weerstand van water tegen de beweging van het platform praktisch nul is vanwege de lage snelheid, kan het worden bevestigd dat het systeem bestaat uit De puppy + het platform Het is een geïsoleerd systeem en het principe van behoud van het lineaire momentum wordt toegepast:

0 = M ∙ V + M ∙ V

Herinnerend dat V = V ' + V je hebt:

0 = -m ∙ V ' + M ∙ V + M ∙ V

Dat wil zeggen: m ∙ v '= (m+m) ∙ v

Daarom v = [m/(m + m)] v 'y v = - (m/m) v = - [m/(m + m)] v'

Numerieke waarden vervangen is:

V = [5/(5 +15)] ∙ 0,5 m/s = 0,125 m/s

Dit is de snelheid waarmee het veerplatform weggaat.

V = -(15/20) ∙ 0,5 m/s = -0,375 m/s

En dit is de snelheid waarmee de puppy het dok nadert.

Referenties

1. Duke universiteit. Systems van deeltjes. Hersteld van: WebHome.Phy.Hertog.Edu.
2. Rex, a. 2011. Fundamentals of Physics. Pearson.
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. Pearson.
4. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren.
5. Tipler, p. (2006). Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd.