Correlatiecoëfficiëntformules, berekening, interpretatie, voorbeeld

Hij correlatiecoëfficiënt In statistieken is het een indicator die de trend van twee kwantitatieve variabelen x en y meet om een ​​relatie van lineariteit of evenredigheid ertussen te hebben.

Over het algemeen zijn de paren variabelen X en Y twee kenmerken van dezelfde populatie. X kan bijvoorbeeld de hoogte zijn van een persoon E en zijn gewicht.

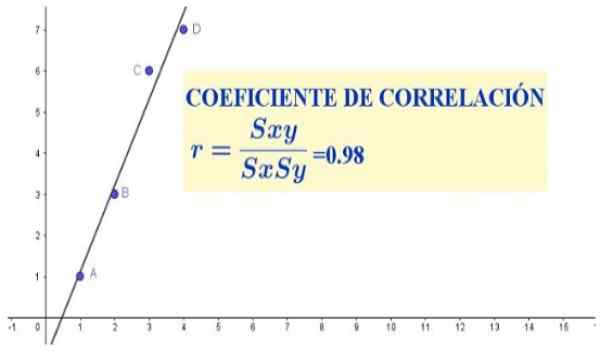
Figuur 1. Correlatiecoëfficiënt voor vier gegevensparen (x, y). Bron: f. Zapata.

In dit geval zou de correlatiecoëfficiënt aangeven of er al dan niet een verhouding van evenredigheid is tussen de lengte en het gewicht van een bepaalde populatie.

De lineaire correlatiecoëfficiënt van Pearson wordt aangegeven met de brief R kleine letters en de minimale en maximale waarden zijn respectievelijk -1 en +1. 

Een waarde r = +1 zou aangeven dat de hele paren (x, y) perfect zijn uitgelijnd en dat wanneer x groeit en in dezelfde verhouding zal groeien. Aan de andere kant, als het gebeurt dat r = -1, zou de set paren ook perfect zijn uitgelijnd, maar in dat geval wanneer X groeit en in dezelfde verhouding afneemt.

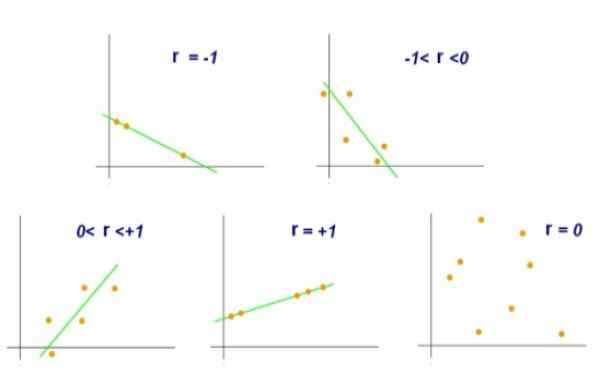Figuur 2. Verschillende waarden van de lineaire correlatiecoëfficiënt. Bron: Wikimedia Commons.

Aan de andere kant zou een waarde r = 0 aangeven dat er geen lineaire correlatie is tussen de variabelen x en y. Hoewel een waarde van r = +0.8 zou aangeven dat de paren (x, y) de neiging hebben om naar de ene kant en een andere lijn te groeperen.

De formule voor het berekenen van de correlatiecoëfficiënt R is als volgt:

Waarbij de teller de covariantie tussen de variabelen X en Y weergeeft, terwijl de noemer het product is van de standaardafwijking voor variabele X en de standaardafwijking voor de variabele en.

Hoe de correlatiecoëfficiënt te berekenen?

De lineaire correlatiecoëfficiënt is een statistisch bedrag dat is opgenomen in wetenschappelijke rekenmachines, in de meeste spreadsheets en statistische programma's.

Kan u van dienst zijn: Hyperbolische paraboloïde: definitie, eigenschappen en voorbeelden

Het is echter handig om te weten hoe de formule die deze definieert, wordt toegepast, en hiervoor wordt een gedetailleerde berekening weergegeven, uitgevoerd op een kleine gegevensset.

En zoals vermeld in de vorige paragraaf, is de correlatiecoëfficiënt de SXY -covariantie gedeeld door het product van de standaardafwijking SX voor de variabelen X en SY voor de variabele en.

Covariantie en variantie

De SXY -covariantie is:

Sxy = [σ (xi -) (yi -)] / (n -1)

Waar de som gaat van 1 naar de n paren (xi, yi). E zijn respectievelijk de rekenkundige kousen van de gegevens xi e yi.

Van zijn kant is de standaardafwijking voor variabele X de vierkantswortel van de variantie van de XI -gegevensset, met i van 1 tot n:

Sx = √ [σ (xi -)^2) / (n -1)]

Evenzo is de standaardafwijking voor de variabele en is de vierkantswortel van de variantie van de Yi -gegevensset, met i van 1 tot n:

Sy = √ [σ (yi -)² ) / (N-1)]

Illustratief geval

Om gedetailleerd de manier aan te tonen om de correlatiecoëfficiënt te berekenen, nemen we de volgende set van vier paar gegevens 

(X, y): (1, 1); (23); (3, 6) en (4, 7).

Eerst berekenen we het rekenkundige gemiddelde voor X en Y, als volgt:

= (1 + 2 + 3 + 4) / 4 = 2.5

= (1 + 3 + 6 + 7) / 4 = 4.25

Vervolgens worden de resterende parameters berekend:

SXY -covariantie

Sxy = [(1 - 2.5) (1 - 4.25) + (2 - 2.5) (3 - 4.25) + (3 - 2.5) (6 - 4.25) +.. ... .(4 - 2.5) (7 - 4.25)] / (4-1)

Sxy = [(-1.5) (-3.25) + (-0.5) (-1.25) + (0.5) (1.75) +.. . 

Kan u van dienst zijn: afleidingregels (met voorbeelden)

.. .(1.5) (2.75)] / (3) = 10.5/3 = 3.5

Standaardafwijking SX

Sx = √ [(-1.5)² + (-0.5)² + (0.5)² + (1.5)²) / (4-1)] = √ [5/3] = 1.29

Standaardafwijking SY

Sx = √ [(-3.25)² + (-1.25)² + (1.75)² + (2.75)²) / (4-1)] = 

√ [22.75/3] = 2.75

Relingcoëfficiënt r

R = 3.5 / (1.29 * 2.75) = 0.98

Interpretatie

In de gegevensset van het vorige geval is er een sterke lineaire correlatie tussen de variabelen X en Y, die zich zowel in de dispersiekrafiek (die te zien is in figuur 1) en in de correlatiecoëfficiënt manifest de eenheid.

In de mate dat de correlatiecoëfficiënt dichter bij 1 of -1 ligt, maakt het gevoel dat de gegevens instellen in een lijn, het resultaat van de lineaire regressie.

Lineaire regressie

De lineaire regressielijn is verkregen van Methode van de minste vierkanten. waarin de parameter regressielijn wordt verkregen uit de minimalisatie van de som van het kwadraat van het verschil tussen de waarde en geschatte en de YI van de N -gegevens.

Aan de andere kant zijn parameters A en B van de regressielijn y = a + bx, verkregen met de methode van de minimale vierkanten,:

*B = sxy / (sx²) Voor de helling

*A = - b voor de kruising van de regressielijn met de as van de en.

Bedenk dat SXY de hierboven gedefinieerde covariantie is en SX² Het is de variantie of het vierkant van de eerder gedefinieerde standaardafwijking. E zijn de rekenkundige middelen van de gegevens x en en respectievelijk.

Voorbeeld

De correlatiecoëfficiënt wordt gebruikt om te bepalen of er een lineaire type correlatie is tussen twee variabelen. Het is van toepassing wanneer de te bestuderen variabelen kwantitatief zijn en ook worden verondersteld een normale typeverdeling te volgen.

Kan u van dienst zijn: correspondentieregel van een functie

Een illustratief voorbeeld dat we hieronder hebben: een maat voor de mate van obesitas is de body mass index, die wordt verkregen door het gewicht van één persoon te delen in kilogrammen tussen de hoogte van hetzelfde in de vierkante eenheden naar het vierkant.

Het is gewenst om te weten of er een sterke correlatie is tussen de lichaamsmassa -index en de concentratie van HDL -cholesterol in bloed, gemeten in millimolen per liter. Hiertoe is een onderzoek gedaan met 533 mensen samengevat in de volgende grafiek, waarin elk punt de gegevens van een persoon vertegenwoordigt.

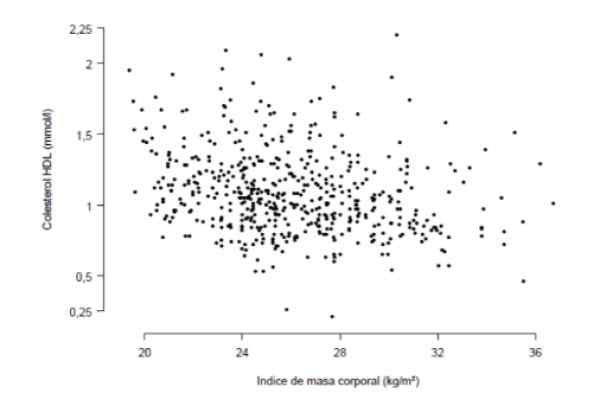figuur 3. IMC -studie en HDL -cholesterol bij 533 patiënten. Bron: Aragonese Institute of Health Sciences (IACS).

Uit de zorgvuldige observatie van de grafiek volgt hieruit dat er een bepaalde lineaire (niet erg gemarkeerde) trend is tussen de HDL -cholesterolconcentratie en de body mass index. De kwantitatieve maat van deze trend is de correlatiecoëfficiënt die voor deze zaak r = -0,276 bleek te zijn.

Referenties

1. González C. Algemene statistieken. Hersteld van: tarwi.La Molina.Edu.pe
2. IACS. Aragonese Institute of Health Sciences. Opgehaald uit: ICS-Aragon.com 
3. Salazar C. en Castillo S. Basisstatistiekenprincipes. (2018). Opgehaald uit: DSPACE.Uce.Edu.EC
4. Superprof. Correlatiecoëfficiënt. Hersteld van: superprof.is
5. USAC. Beschrijvende statistiekenhandleiding. (2011). Hersteld van: statistieken.engineering.USAC.Edu.GT
6. Wikipedia. Pearson correlatiecoëfficiënt. Hersteld van: is.Wikipedia.com.