Hoe u het percentage kunt krijgen? Voorbeelden en oefeningen

Kan Krijg een percentage Met verschillende methoden. U kunt snel alleen 10% van elk nummer berekenen wanneer u uw decimale komma een positie naar links verplaatst. 10% van 100 is bijvoorbeeld 10; 10% van 1000 is 100.

Als u meer complexe percentages zoals 36% van 25 of 250% van 20 wilt berekenen, zijn andere methoden nodig. Voor gevallen waarin het 10% -systeem niet van toepassing is, kunnen de volgende methoden in aanmerking worden genomen.

Figuur 1. Kortingen met verschillende percentages. Hoeveel redden we elkaar?. Bron: Pixabay.

De term percentage betekent een bepaald deel van elke honderd en verwijst naar de rekenkundige operatie die wordt uitgevoerd om het genoemde deel te vinden. Bijvoorbeeld 20% ("twintig procent") wordt gelezen in peso's, dit betekent dat 20 peso's worden verdisconteerd voor elke 100 pesos.

Het percentage dient om te berekenen welk deel van het totaal een bedrag vertegenwoordigt. In dit geval wordt het totaal op de schaal van 100 gebracht en het percentage informeert hoeveel, op basis van die 100, het deel is dat moet worden berekend.

Laten we eens kijken hoe het wordt gedaan met deze voorbeelden. In de eerste plaats doen we het in de vorm van een fractie:

• 20% = 20/100
• 5% = 5 /100
• 0,7% = 0,7 / 100
• 100% = 100 /100

Merk op dat 100% gelijk is aan 1. Maar de percentages kunnen ook worden geschreven decimaal:

• 20% = 0,20
• 5% = 0,05
• 0,7% = 0,007
• 100% = 1,0

Wanneer het percentage van een bepaald aantal wordt uitgedrukt, eenvoudigweg De komma beweegt Van die nummer twee plaatsen links. In het percentage, de evenredigheidsregel:

20% is dus 20 van de 100, dus:

20% van 100 is 20, 20% van 200 is 40, 20% van 300 is 60, 20% van 50 is 10.

Algemene regel voor 20 % van enig bedrag

20% x is x *(20/100) = x *0,2 = 0,2 *x

Deze regel kan zich gemakkelijk uitstrekken om een ​​ander gewenst percentage te vinden. Laten we eens kijken hoe in de volgende sectie.

Oefening opgelost met formule om n% te berekenen 

Een formule om zo snel mogelijk samen te vatten en snel elk percentage te berekenen N is:

N % =(A * n)/100

U wilt bijvoorbeeld 25% van 400 berekenen

Dan n = 25 en a = 400, resulterend in (400*25)/100 = 100

Voorbeeld

Welk percentage van 60 is 24?

Oplossing

Wat wordt gevraagd is gelijk aan het vragen wat de n% van 60 is die 24 geeft?

We stellen de algemene formule voor:

60 * N / 100 = 24

We wissen N Met deze procedure:

-De 100 die verdeelt in lid IZiédo Van gelijkheid, ga naar het lid rechts vermenigvuldigen. 

-En de 60 die zich vermenigvuldigt in het lid links Ga naar het lid rechts verdeling.

N = 24 *100/60 = 2400 /60 = 240/6 = 6 *40/6 = 40

Er wordt geconcludeerd dat 40% van de 60 24 is.

Opgelost percentage berekeningsoefeningen 

Hieronder staan ​​eenvoudige oefeningen om de eerder genoemde te oefenen.

Het kan je van dienst zijn: de 15 meest populaire legendes en mythen

Oefening 1

Vind 50% van 90.

Oplossing

Hier x = 90, n = 50 % en vervangen:

90 * 50% = 90 * (50/100) = 4500 /100 = 45 

Dit is vrij eenvoudig, omdat 50 % van elk bedrag de helft van dat bedrag is en de helft van 90 45 is.

Oefening 2

Zoek 30% van 90.

Oplossing

90 * 30% = 90 * (30/100) = 2700 /100 = 27

Percentage neemt toe

Het komt vaak voor in het dagelijks leven om te luisteren naar de toename van iets, bijvoorbeeld een toename van de productie, een salarisverhoging of de opkomst van een product. Het wordt bijna altijd uitgedrukt in procentuele vorm.

Een bepaald product kostte bijvoorbeeld € 300, maar leed een stijging van 30%. We vragen ons af: wat is de nieuwe productprijs?

De eerste is om het gedeelte te berekenen dat overeenkomt met de toename. Omdat de toename 30 delen van 100 is, dus de toename van de toename, gebaseerd op de oorspronkelijke prijs van 300, is drie keer de 30 delen, dat wil zeggen 3*30 = 90.

Het product verhoogde € 90, dus de nieuwe uiteindelijke prijs is wat de stijging eerder kostte:

Nieuwe prijs = oude prijs + € 90 = € 390

We kunnen een formule bouwen voor de berekening van de procentuele toename. We gebruiken letters om prijzen te symboliseren, zoals deze:

-F is de uiteindelijke waarde

-Je is de initiële waarde en

-N is de toename van de toename.

Met deze namen zou de uiteindelijke waarde als volgt worden berekend:

f = i + (i* n / 100)

Maar hoe Je Het wordt in beide termen herhaald, het kan als een gemeenschappelijke factor worden beschouwdOm deze andere uitdrukking te verkrijgen, even geldig:

F = i * (1 + n / 100)

Laten we verifiëren met de reeds opgeloste zaak, het product dat € 300 kost en met 30% is gestegen. Zo zorgen we ervoor dat de formule goed werkt:

Eindprijs = F = € 300 * (1 + 30/100) = € 300 * (1 + 0.3) = € 300 * 1,3 = € 390

Oefening 3

Een werknemer verdiende € 1500, maar werd gepromoveerd en zijn salaris had een verhoging van 20%. Wat is uw nieuwe salaris?

Oplossing

Laten we de formule toepassen:

F = € 1500 * (1 + 20/100) = € 1500 * (1 + 0.2) = € 1500 * 1.2 = € 1800

Het nieuwe salaris van de werknemers is € 1800.

Percentage neemt af

In het geval van afnames, de formule voor de berekening van de uiteindelijke waarde F van een bepaald initiële bedrag Je die een afname van een afname van N% is:

F = i * (1 - n / 100)

Opgemerkt moet worden dat het positieve teken (+) van de formule in de vorige sectie is vervangen door een negatief teken (-).

Figuur 2. Percentage korting kennis. Bron: Pixabay

Oefening 4

Een product markeerde € 800, maar ontving een korting van 15%. Wat is de nieuwe productprijs?

Oplossing 4

De uiteindelijke prijs volgens de formule is:

F = € 800 * (1 - 15/00) = € 800 * (1 - 0,15) = € 800 * (0,85) = € 680

De uiteindelijke prijs met de korting van 15% is € 680, wat een besparing van € 120 vertegenwoordigt.

Opeenvolgende percentages

Het lijkt erop dat een bepaald bedrag een percentagevariatie lijdt en een andere wordt toegepast, ook een percentage. Bijvoorbeeld een product dat twee procent kortingen op een rij heeft gehad. Een ander voorbeeld is dat van een werknemer die twee opeenvolgende salarisverhogingen had.

Kan u van dienst zijn: belangrijker Yucatan -economische activiteiten

- Opeenvolgende percentage neemt toe

De oplossingsbasis van deze gevallen is hetzelfde als de unieke toename, maar er moet rekening mee worden gehouden dat de tweede procentuele toename wordt uitgevoerd op de uiteindelijke waarde van de eerste toename.

Stel dat een product dat de eerste 10% en vervolgens 5% steeg,. Het is onjuist om te zeggen dat het een toename van 15%leed, het was eigenlijk meer dan dit percentage.

De formules voor de uiteindelijke waarde zouden zo van toepassing zijn:

-Eerst wordt de uiteindelijke waarde van de eerste stijging van N1% berekend

F1 = I + I * N1 / 100

-En dan, om de uiteindelijke waarde van de tweede toename van N2%te vinden, wordt de uiteindelijke waarde van F1 als een beginwaarde genomen. Daarom:

F2 = f1 + f1 * n2 /100 

Oefening 5

Een boek kostte oorspronkelijk € 55, maar vanwege het succes en de grote vraag leed het twee opeenvolgende verhogingen voor de oorspronkelijke prijs. De eerste stijging was 10% en de tweede van 20%. Wat is de uiteindelijke prijs van het boek?

Oplossing

-Eerste toename:

F1 = € 55 * (1 + 10/00) = € 55 * 1.1 = € 60,5

-Tweede toename

F2 = € 60,5 * (1 + 20/100) = € 60,5 * 1.2 = € 72.6

De uiteindelijke prijs is € 72,6.

Oefening 6

In verwijzing naar de vorige oefening. De twee opeenvolgende stijgingen: tot welk percentage van een unieke verhoging ten opzichte van de oorspronkelijke boekprijs komt overeen?

Oplossing

Als we N% bellen naar het percentage unieke toename, is de formule die deze unieke procentuele toename relateert aan de oorspronkelijke waarde en de uiteindelijke waarde is:

F2 = i *(1 + n / 100) 

Het is te zeggen:

€ 72,6 = € 55 + 55 € * (n / 100)

Als we de toename van de toename n% = (n /100) opruimen, hebben we:

(N / 100) = (€ 72,6 - € 55) / 55 € = 17.€ 6 / € 55 = 0,32

Daarom:

N = 0,32 * 100 = 32

Voor de prijs van het boek werd een totale procentuele stijging van 32% toegepast. Merk op dat deze toename groter is dan de som van de twee opeenvolgende procentuele toename.

- Opeenvolgende percentage kortingen

Het idee is vergelijkbaar met dat van opeenvolgende percentage toename. De tweede percentage korting moet altijd worden toegepast op de uiteindelijke waarde van de eerste korting, laten we eens kijken naar een voorbeeld:

Oefening 7

Een korting van 10% gevolgd door een tweede korting van 20% op een object, waaraan unieke percentagekorting het equivalent is?

Oplossing

-Eerste korting:

F1 = I - I * N1 / 100  

-Tweede korting

F2 = F1 - F1 * N2 / 100

De eerste vergelijking vervangen in de tweede overblijfselen:

f2 = (i - i * n1 / 100) - (i - i * n1 / 100) * n2 / 100

Als we deze uitdrukking ontwikkelen, krijgen we:

f2 = i - i* n1 / 100 - i* n2 / 100 + i* (n1 / 100) (n2 / 100) 

Gemeenschappelijke factor trekken Je:

F2 = I * (1- N1% - N2% + N1% * N2%)

Ten slotte worden de in de vraag aangegeven percentages vervangen:

F2 = i * (1 - 10% - 20% + 10% * 20%) = i * (1 - 0,1 - 0,2 + 0,1 * 0,2)

f2 = i * (1 - 0.3 + 0.02) = i * (0.72) = i * (1 - 0.28) = i * (1 - 100/ 100) = i * (1 - 28%)

Met andere woorden, opeenvolgende kortingen van 10% en 20% komen overeen met een unieke korting van 28%.

Geavanceerde oefeningen

Laten we deze oefeningen alleen proberen als de ideeën van de vorige duidelijk genoeg zijn geweest.

Het kan je van dienst zijn: eenvoudige en mooie geografische covers, covers, afbeeldingen

Oefening 8

De basis van een driehoek meet 10 cm en hoogte 6 cm. Als de basislengte afneemt met 10%. In welk percentage moet de hoogte worden verhoogd, zodat het driehoeksgebied niet verandert?

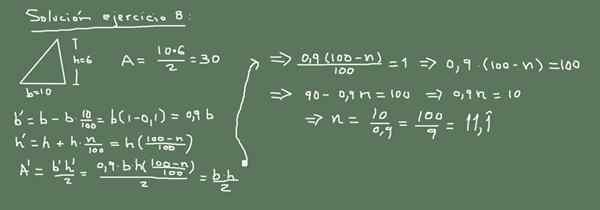figuur 3. Alternatieve oplossing voor oefening 8. Bereid door f. Zapata.

Oplossing 8

Het originele driehoeksgebied is:

A = (10 cm * 6 cm) / 2 = 30 cm²

Nu, als de basis met 10%afneemt, is de nieuwe waarde ervan:

Nieuwe basis = 10 - (10/100) x 10 = 9 cm.

De nieuwe hoogtewaarde is X en het oorspronkelijke gebied moet ongewijzigd worden gehouden, zodat:

(9 cm * x) /2 = 30 cm²

Dan wordt de waarde van X gewist als:

X = 60 cm² / 9 cm = (20/3) cm = 6.666 cm

Wat een toename van 0,666 betekent in vergelijking met de oorspronkelijke waarde. Laten we nu eens kijken welk percentage hiervan vertegenwoordigt:

6.666 = 6 + (6 * n/100) 

6.666 -6 = 6 * n/100

0.666 = 6 * N/100

N/100 = 0,111

N = 11.1

Het antwoord is: de hoogte moet worden verhoogd met 11,1% om het driehoeksgebied hetzelfde te blijven.

Oefening 9

Als het salaris met 20%wordt verhoogd, maar dan de belastingkorting 5%, wat is de reële toename die de werknemer ontvangt?

Oplossing 

Eerst berekenen we de toename van N1%:

F1 = I + I * N1 / 100

Dan passen we de N2% -korting toe:

F2 = F1 - F1 * N2 / 100

De eerste vergelijking wordt in de tweede vervangen:

f2 = i + i * n1 / 100 - (i + i * n1 / 100) * n2 / 100

De vorige uitdrukking ontwikkelt zich:

f2 = i + i * n1 / 100 - i * n2 / 100 - i * (n1 / 100) * (n2 / 100)

Eindelijk wordt het verwijderd Je Gemeenschappelijke factor en de waarden van N1 = 20 en N2 = 5 die in de verklaring verschijnen, worden vervangen:

F2 = i (1 + 0.2 - 0,05 - 0,2* 0,05) = i* (1 + 7/50) = i* (1 + 14/100) = i* (1 + 14%)

De werknemer ontving een netto toename van 14%.

Oefening 10

Bepaal wat het handigst is tussen deze twee opties:

i) T -shirts verwerven met elk 32 % korting.

Ii) Koop 3 t -shirts voor de prijs van 2.

Oplossing 

We analyseren elke optie afzonderlijk en kiezen vervolgens de meest economische:

i) Laat X de huidige prijs van een shirt zijn, een korting van 32 % vertegenwoordigt een uiteindelijke prijs van XF:

Xf = x - (32/100) x = x - 0.32x = 0.68x

Het kopen van 3 shirts betekent bijvoorbeeld uitgeven van 3 x 0.68 x = 2.04X

ii) Als X de prijs van een shirt is, betaal je voor 3 shirts gewoon 2x.

Stel dat een shirt 6 euro waard is, met de korting van 32 % zou het 4 waard zijn.08 euro. Koop 1 t -shirt is geen geldige optie in de 3 × 2 -aanbieding. Dus als u maar 1 shirt wilt kopen, heeft de korting de voorkeur.

Maar als wat je wilt voor tientallen is, is de 3 × 2 -aanbieding gewoon een beetje goedkoper. 6 t -shirts met de korting zouden bijvoorbeeld 24 uitgaan voor 24.48 euro, terwijl ze met het 3 × 2 -aanbod 24 euro kosten

Referenties

1. Eenvoudig klaslokaal. Het percentage. Opgehaald uit: klaslokaal.com
2. Baldor a. 2006. Praktische theoretische rekenkunde. Culturele edities.
3. Educa -kinderen. Hoe u percentages kunt leren berekenen. Hersteld van: educapeques.com
4. Gutiérrez, g. Financiële wiskunde -aantekeningen. Hersteld van: CSH.IZT.UAM.mx
5. Slimme teken. Percentage: wat is en hoe wordt berekend. Hersteld van: Smartick.is