Wordt genoemd Aanzienlijke aantallen naar de hoeveelheid cijfers die de Bidderij van een nummer. Hoe meer getallen de hoeveelheid bekend is met de grootste precisie. Ter herinnering, de Mantisa is het figuur dat gepaard gaat met de kracht van 10 wanneer het nummer in wetenschappelijke notatie is geschreven.

Laten we bijvoorbeeld nummer 0 nemen.00376, die is geschreven als 3.76 x 10 ^-3. De Mantisa is 3.76 en het aantal heeft in totaal 3 significante cijfers. Het nummer 0.129 heeft ook 3 belangrijke cijfers, terwijl 4.5 heeft slechts 2.

Figuur 1. Wetenschappelijke rekenmachines tonen nooit het aantal significante cijfers van een operatie. Bron: PiqSels.

En wat er gebeurt als het nummer heel is? Het betekent dat het bekend is met alle mogelijke precisie, met andere woorden, het heeft oneindige precisie. Door mensen, dieren of objecten zoals boeken en telefoons te tellen, is het resultaat bijvoorbeeld een geheel getal en een nauwkeurig nummer.

Als we zeggen dat er in een bioscoop 110 mensen naar een film kijken, is dit het exacte aantal, noch meer of minder, en heeft 3 belangrijke figuren.

Aanzienlijke cijfers worden afgehandeld door enkele eenvoudige regels die worden onthouden met een beetje oefening, zoals we dan zullen zien.

[TOC]

Regels om de significante cijfers van een aantal te bepalen

Regel 1

De voorgaande nullen tellen niet als een significant figuur, dus 0.045 en 4.5 Ze hebben beide 2 significante cijfers, omdat deze vanaf links beginnen te worden geteld en beginnend bij het eerste verschillende cijfer van nul.

Regel 2

De achterste nullen (aan de rechterkant) naar het eerste significante cijfer tellen als een significant figuur (zolang het gerechtvaardigd is door de nauwkeurigheid van het meetinstrument).

Ten slotte worden de nullen die zich in het midden bevinden ook als aanzienlijk cijfer geteld.

Regel 3

Voor de in wetenschappelijke notatie geschreven getallen, zijn alle mantisa -cijfers significant en de exponent heeft geen invloed op de precisie.

Het kan u van dienst zijn: gemiddelde snelheid: formules, hoe het wordt berekend en opgelost

Regel 4

Wanneer bewerkingen met decimalen worden uitgevoerd, bijvoorbeeld door gebieden of andere vergelijkbare bewerkingen te berekenen, moet het resultaat hetzelfde aantal significante cijfers hebben als het bedrag met het laagste aantal significante cijfers die aan de operatie hebben deelgenomen. Deze regel is geldig voor elke rekenkundige bewerking.

Regel 5

Het aantal van het aantal heeft geen invloed op het aantal significante cijfers.

We zullen onmiddellijk enkele voorbeelden hiervan en alle andere regels zien.

Voorbeelden

voorbeeld 1

Zoek hoeveel significante cijfers er in elk van deze getallen zijn.

a) 876

b) 1000.68

C) 0.00005026

d) 4.8

e) -6.99

Antwoorden

A) 876 heeft 3 belangrijke cijfers.

b) 1000.68 heeft 6 significante cijfers, sinds nullen in de middelste telling als zodanig.

c) In plaats daarvan 0.00005026 heeft 4 belangrijke cijfers. Merk op dat de 5 nullen links van de 5 niet worden geteld als een significant figuur, in plaats daarvan op de 0 tussen 5 en 2 ja.

d) 4.8 heeft 2 belangrijke cijfers.

e) -6.99 heeft 3 belangrijke cijfers.

Voorbeeld 2

Het is gebruikelijk om maatregelen te nemen, zoals metrische banden, horloges, thermometers, schalen, enzovoort op de stijl. Hoeveel belangrijke cijfers moeten we de bedragen rapporteren die we op deze manier meten?

Antwoord

Het hangt af van de waardering van het instrument waarmee het wordt gemeten. Laten we een voorbeeld geven: meet de externe diameter van een buis, met een afgestudeerde regel en met Vernier of King's Foot.

De Vernier is een instrument dat de lengtes zeer precies meet omdat hij een extra kleine schaal heeft, genaamd nonius, wat bij het meten een grotere fijnheid mogelijk maakt bij het meten.

Het is preciezer dan een afgestudeerde regel omdat we daarmee meer belangrijke figuren van een bepaalde lengte kunnen leren.

Daarom heeft het geen zin om een ​​omtrek te melden van bijvoorbeeld 35.88 cm als we het meten met een meetlint, omdat dit instrument niet precies genoeg is om zoveel belangrijke cijfers te melden.

Kan u van dienst zijn: statisch: geschiedenis, welke studies, toepassingen, wetten

De waardering van de meetlint wordt gegeven door:

Voor een meetlint of een millimeterregel, a = 1 mm, dat is de tiende van een centimeter. De perimeter gemeten met meetlint moet worden gerapporteerd als 35.9 cm.

Voorbeeld 3

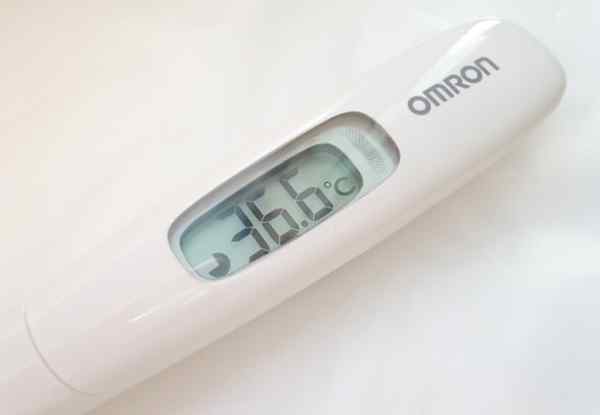
Hoeveel belangrijke cijfers heeft het lezen gemaakt met de digitale thermometer?

Antwoord

De thermometer van de figuur biedt temperatuurmetingen met drie cijfers. Voor zover getoonde mate echter 36.6 ºC, alleen de eerste twee cijfers van links naar rechts zijn nauwkeurig, omdat het decimaal wordt beïnvloed door de fout van waardering van het instrument, dat meestal wordt aangegeven in de achterkant van dezelfde of in de operationele handleiding.

Het gebruikelijke voor het type digitale instrument is een fout van 0 waardering.1 ºC. Dit is voldoende om er zeker van te zijn dat er geen koorts is.

Figuur 2. Digitale thermometer waarvan de metingen 3 belangrijke cijfers zijn. Bron: Pxhere.

Regels om getallen af ​​te ronden

Wanneer een calculator wordt gebruikt om berekeningen uit te voeren met verkregen maatregelen, is het niet correct om het resultaat te geven met behulp van alle cijfers die op het scherm verschijnen.

Alleen degenen die elkaar precies kennen, worden behouden, omdat alleen die een ware betekenis hebben. Dan is het noodzakelijk om de resultaten af ​​te ronden om te passen. Deze regels zijn:

-Als het nummer dat volgt, is het te behouden cijfer gelijk aan of groter dan 5, Aan dit cijfer wordt toegevoegd 1.

Bijvoorbeeld door af te ronden 3.786 Om twee decimalen te hebben, willen we de cijfers behouden tot 8. Omdat het volgende nummer (6) groter is dan 5, wordt de 8 8 + 1 = 9 en blijft het nummer 3.79.

-Wanneer het nummer dat het te behouden cijfer volgt, is minder dan 5, Het cijfer is hetzelfde.

Kan u van dienst zijn: Joule -effect: uitleg, voorbeelden, oefeningen, toepassingen

Als we 1 willen ronden.27924 om slechts 3 decimalen te hebben, dit wordt bereikt door 9 te bereiken, gevolgd door een 2. Omdat de 2 minder dan 5 is, verdwijnen deze decimalen en is het afgeronde nummer 1.279.

Oefening opgelost

Een eettafel heeft de vorm en afmetingen aangegeven in de bijgevoegde figuur. Er wordt gevraagd om zijn gebied te berekenen met behulp van de regels van de operaties met belangrijke cijfers.

Oplossing

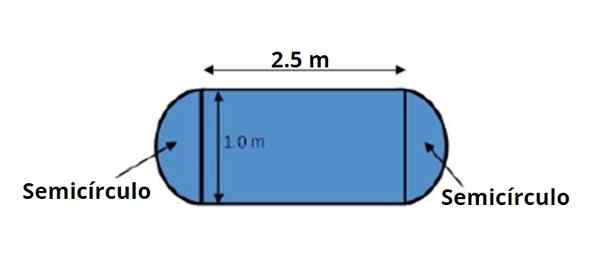figuur 3. Een tabel heeft de vorm en afmetingen die in de figuur worden aangegeven, merk op dat deze bekend zijn met twee significante cijfers. Bron: f. Zapata.

Het tafelgebied kan worden onderverdeeld in een centraal rechthoekig gebied en twee semicirkels, één aan elke kant, die samen 1 volledige cirkel maken.

We zullen bellen₁ aan het rechthoekige gebied, gegeven door:

NAAR₁ = Basis × Hoogte = 2.5 m x 1.0 m = 2.5m²

Van zijn kant is het cirkelgebied, dat gelijkwaardig is aan dat van 1 halve cirkel vermenigvuldigd met 2:

NAAR₂ = π × radio²

De diameter van een van de semicirkels is 1.0 m, daarom is de straal 0.50 m. De diameter kan ook rechtstreeks worden gebruikt om het gebied te berekenen, in dit geval:

NAAR₂ = (π × diameter²) / 4

In elk geval:

NAAR₂ = [π x (1.0 m)²] / 4 = 0.785398163 m²

Alle cijfers aangeboden door de rekenmachine werden gebruikt. Nu voegen we toe aan₁ al₂ Voor de totale oppervlakte van de tabel:

A = (2.5 + 0.785398163) m² = 3.285398163 m²

Aangezien de dimensies van de tabel bekend zijn met 2 significante cijfers, heeft het geen zin om het resultaat uit te drukken met alle decimalen die de calculator geven, die nooit het aantal significante cijfers van een resultaat geeft.

Wat moet worden gedaan, is om het gebied te omzeilen, zodat het hetzelfde aantal significante cijfers heeft als de afmetingen van de tabel, dat wil zeggen 2. Daarom wordt het uiteindelijke resultaat als volgt gerapporteerd:

A = 3.3 m²

Referenties

1. Bauer, W. 2011. Fysica voor engineering en wetenschappen. Deel 1. MC Graw Hill.
2. Figueroa, D. (2005). Serie: Physics for Science and Engineering. Deel 1. Kinematica. Uitgegeven door Douglas Figueroa (USB).
3. Fisicalab. Aanzienlijke cijfers en afronding. Hersteld van: fisicalab.com.
4. Giancoli, D.  2006. Fysica: principes met toepassingen. 6e. Ed Prentice Hall.
5. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Volume1.