Inelastische botsingen in een dimensie en voorbeelden

De Niet -elastische schokken of inelastische botsingen zijn een korte en intense interactie tussen twee objecten waarin de hoeveelheid beweging wordt bewaard, maar niet de kinetische energie, waarvan een percentage wordt omgezet in een ander type energie.

Schokken of botsingen komen vaak van aard. Subatomaire deeltjes botsen bij zeer hoge snelheden, terwijl veel sporten en games bestaan ​​uit continue botsingen. Zelfs sterrenstelsels kunnen botsen.

Figuur 1. Testauto botsing. Bron: Pixabay

Eigenlijk wordt de hoeveelheid beweging behouden in elk type botsing, zolang de deeltjes in botsing zijn gekomen door een geïsoleerd systeem. Dus in deze zin is er geen probleem. Nu hebben objecten kinetische energie geassocieerd met de beweging die ze hebben. Wat kan er met die energie gebeuren tijdens het crashen?

De interne krachten die plaatsvinden tijdens de botsing tussen de objecten zijn intens. Wanneer wordt gezegd dat kinetische energie niet wordt bewaard, betekent dit dat het wordt omgezet in andere soorten energie: bijvoorbeeld in geluidsenergie (een botsing van het apparaat heeft een onderscheidend geluid).

Meer gebruiksmogelijkheden voor kinetische energie: warmte door wrijving, en natuurlijk de onvermijdelijke vervorming door objecten tijdens het botsen, zoals autolichamen in de figuur hierboven.

[TOC]

Voorbeelden van inelastische botsingen 

- Twee massa's plasticine die botsen en elkaar ontmoeten, als één stuk na de crash bewegend.

- Een rubberen bal die tegen een muur of vloer stuitert. De bal vervormt bij het beïnvloeden van het oppervlak.

Niet alle kinetische energie wordt omgezet in andere soorten energie, behalve op enkele uitzonderingen na. Objecten kunnen bij een bepaalde hoeveelheid van deze energie blijven. Later zullen we zien hoe we het percentage kunnen berekenen.

Wanneer de stukken die botsen met elkaar verbonden zijn, wordt de botsing perfect inelastisch genoemd en beiden worden meestal samen bewegend.

Perfect inelastische botsingen in een dimensie

De botsing van de figuur toont twee objecten van verschillende massa's M₁ En M₂, naar elkaar bewegen met snelheden v_I1 En v_I2 respectievelijk. Alles gebeurt aan de horizontale, dat wil zeggen, het is een botsing in een dimensie, de eenvoudigste om te bestuderen.

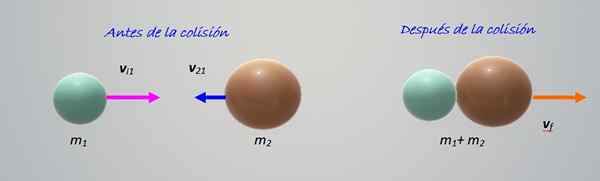Figuur 2. Botsing tussen twee deeltjes van verschillende massa's. Bron: zelf gemaakt.

De objecten botsen en worden vervolgens verenigd om naar rechts te gaan. Het is een perfect inelastische botsing, dus het is voldoende dat we de hoeveelheid beweging behouden:

P_of = P_F

De hoeveelheid beweging is een vector waarvan eenheden zijn.S. In de beschreven situatie kan de vectornotatie worden afgegeven omdat het botsingen in een dimensie is:

Het kan u van dienst zijn: eenvoudige fysica-experimenten (primaire universiteit)

MV_of = MV_F

De hoeveelheid beweging van het systeem is de vectorsom van de hoeveelheid beweging van elk deeltje.

M₁ v_I1  + M₂ v_I2 = (m₁ + M₂) v_F

De uiteindelijke snelheid wordt gegeven door:

v_F = (m₁ v_I1  + M₂ v_I2)/ (M₁ + M₂))

Restitutiecoëfficiënt

Er is een hoeveelheid die kan aangeven hoe elastisch een botsing is. Het gaat over Restitutiecoëfficiënt, die wordt gedefinieerd als de negatieve verhouding tussen de relatieve snelheid van de deeltjes na de crash en de relatieve snelheid vóór de crash.

Laat je₁ en jij₂ De respectieve snelheden van de deeltjes aanvankelijk. En zijn v₁ en v₂ de respectieve uiteindelijke snelheden. Wiskundig kan de restitutiecoëfficiënt als volgt worden uitgedrukt:

De restitutiecoëfficiënt is een extra bedrag, omdat het de verhouding tussen snelheden is. Maar de verstrekte informatie is erg interessant:

- Als ε = 0 gelijk is aan het vermelden van die v₂ = V₁. Het betekent dat de uiteindelijke snelheden hetzelfde zijn en de botsing niet -elastisch is, zoals beschreven in de vorige sectie.

- Wanneer ε = 1 betekent dat relatieve snelheden zowel voor als na de crash niet veranderen, is de botsing in dit geval elastisch.

- En als 0 < ε < 1 parte de la energía cinética de la colisión se transforma en alguna otra de las energías mencionadas anteriormente.

Hoe u de restitutiecoëfficiënt kunt bepalen?

De restitutiecoëfficiënt is afhankelijk van de klasse materialen die bij de botsing betrokken zijn. Een zeer interessante test om te bepalen hoe elastisch een materiaal is om ballen te maken, is om de bal op een vast oppervlak te laten vallen en de reboundhoogte te meten.

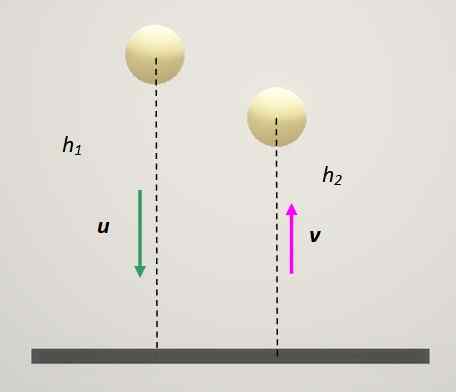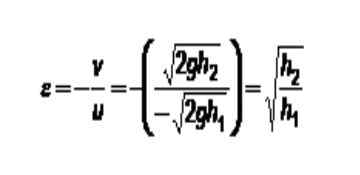
figuur 3. Methode om de restitutiecoëfficiënt te bepalen. Bron: zelf gemaakt.

In dit geval heeft de vaste plaat altijd snelheid 0. Als deze index 1 hieraan wordt toegewezen en de bal is: Index 2 blijft:

De initiële snelheid hangt af van de hoogte H₁ waaruit hij viel:

Het negatieve teken geeft de richting aan. En de uiteindelijke snelheid is gerelateerd aan de maximale hoogte H₂ Dat bereikt in de rebound:

Vervangen in de restitutiecoëfficiënt die u hebt:

Explosies

In het begin is gesuggereerd dat alle kinetische energie kan worden getransformeerd door naar andere soorten energie te gaan. Energie wordt immers niet vernietigd. Is het mogelijk dat objecten die bij beweging kwamen botsen en samen een enkel object vormen dat plotseling in rust is? Dit is niet zo eenvoudig om je voor te stellen.

Het kan u van dienst zijn: Dynamics: History, What Studies, Laws and Theories

Laten we ons echter voorstellen wat er achteruit gebeurt, zoals in een film die in de rug wordt gezien. Toen was het object aanvankelijk rust en explodeert vervolgens fragmenteren in verschillende delen. Deze situatie is perfect mogelijk: het is een explosie.

Zodat een explosie kan worden beschouwd als een perfect inelastische botsing die achteruit in de tijd wordt gezien. De hoeveelheid beweging wordt ook bewaard, die kan bevestigen dat:

P_of = P_F

Opgeloste voorbeelden

-Oefening 1

Het is bekend uit metingen dat de stalen restitutiecoëfficiënt 0 is.90. Een stalen bal wordt gedropt van 7 m hoog op een vaste plaat. Berekenen:

a) tot welke hoogte zal stuiteren.

b) Hoe lang duurt het tussen het eerste contact met het oppervlak en de tweede.

Oplossing

a) De vergelijking die eerder werd afgeleid in de sectie over de bepaling van de restitutiecoëfficiënt wordt gebruikt:

Hoogte is verdwenen H₂:

0.90² . 7 m = 5.67 m

b) Om de 5 op te heffen.67 meter een snelheid gegeven door:

Waar vandaan:

En de tijd die nodig is om deze hoogte te bereiken is:

T _Maximaal = V_of/ g = (10.54/9.8 s) = 1.08 s.

De tijd die nodig is om terug te keren is hetzelfde, daarom de totale tijd om de 5 te uploaden.67 meter en terugkeren naar het startpunt is twee keer de maximale tijd:

T_vlucht = 2.15 s.

-Oefening 2

De figuur toont een blok van massa van massa M die aan de rest van de draden van lengte L als slinger hangt. Dit wordt de ballistische slinger genoemd en dient om de snelheid V van binnenkomst een massa massa m te meten. Hoe hoger de snelheid waarmee de kogel het blok beïnvloedt, op een hogere hoogte h zal dit worden gebouwd.

De beeldkogel is ingebed in het blok, daarom is het een volledig inelastische schok.

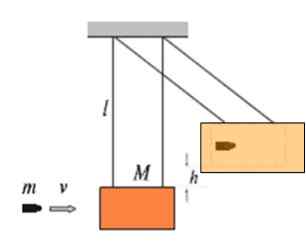Figuur 4. De ballistische slinger.

Neem aan dat een 9 9.72 g impact tegen het massablok 4.60 kg, dan stijgt de set tot 16.8 cm van de evenwichtspositie. Wat is de snelheid v van de kogel?

Oplossing

Tijdens de botsing wordt de hoeveelheid beweging behouden en of_F Het is de snelheid van de set, zodra de kogel in het blok is ingebed:

P_of = P_F

Het blok rust in eerste instantie, terwijl de kogel met snelheid naar het doel is gericht v:

M.v + m.0 = (m + m) u_F

 

Het is niet bekend of_F Zelfs, maar na botsing wordt mechanische energie bewaard, dit is de som van zwaartekrachtpotentiaal energie en kinetische energie K:

Kan u van dienst zijn: som van vectoren: grafische methode, voorbeelden, opgeloste oefeningen

Eerste mechanische energie = uiteindelijke mechanische energie

EN_mo = E_MF

OF_of + K_of = U_F + K_F

Gravitationele potentiële energie hangt af van de hoogte waarop de set bereikt. Voor de evenwichtspositie is de initiële hoogte die daarom als referentieniveau wordt genomen, daarom:

OF_of = 0

Dankzij de kogel heeft de set kinetische energie K_of, die zwaartekracht potentieel energie wordt wanneer de set zijn maximale hoogte bereikt H. Kinetische energie wordt gegeven door:

K = ½ mV²

Aanvankelijk is kinetische energie:

K_of = (1/2) (m+m) u_F²

Onthoud dat de kogel en het blok een enkel massaobject vormen M+ M. De zwaartekracht potentieel energie wanneer ze op hun maximale hoogte hebben bereikt, is:

OF_F = (m + m) gh

Daarom:

K_of = U_F

(1/2) (m+m) u_F² = (m + m) gh

Nu wordt dit resultaat in uitdrukking vervangen door v die in het begin verdwenen, door het behoud van de hoeveelheid beweging:

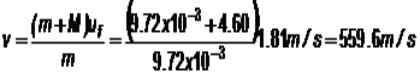
-Oefening 3

Het object van de figuur explodeert in drie fragmenten: twee van gelijke massa m en één groter van massa 2m. De figuur geeft de snelheden aan van elk fragment na de explosie. Wat was het eerste doel van het object?

Figuur 5. De steen die in 3 fragmenten explodeert. Bron: zelf gemaakt.

Oplossing

Dit probleem vereist het gebruik van twee coördinaten: X En En, Omdat twee van de fragmenten verticale snelheden hebben, terwijl de resterende horizontale snelheid heeft.

De totale massa van het object is de som van de massa van alle fragmenten:

M = m + m + 2m = 4m

De hoeveelheid beweging wordt zowel op de X -as als op de Y -as bewaard, deze wordt afzonderlijk voorgesteld:

1. 4m. of_X= M V₃
2. 4m. of_En = m. 2V₁ - 2m. v₁

Merk op dat het grote fragment naar beneden gaat met V1 -snelheid, om op dit feit te wijzen dat een negatief teken is geplaatst.

Uit de tweede vergelijking volgt het onmiddellijk dat of_En = 0, En de eerste is onmiddellijk duidelijk:

Het eerste doel van het object was u_of = u_X = V₃/4.

Referenties

1. Giancoli, D.  2006. Fysica: principes met toepassingen. 6^e. Ed Prentice Hall. 175-181
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 135-155.
3. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^NA Cengage leren. 172 -182
4. Tipler, p. (2006) Natuurkunde voor wetenschap en technologie. 5e ed. Deel 1. Redactioneel teruggekeerd. 217-238
5. Tippens, p. 2011. Fysica: concepten en toepassingen. 7e editie. MacGraw Hill. 185 -195