Chi-kwadraat (χ²) verdeling, hoe het wordt berekend, voorbeelden

Het bewijs Chi Squared of ji-square (χ², Waar χ de Griekse brief is die "chi" wordt genoemd) wordt gebruikt om het gedrag van een bepaalde variabele te bepalen en ook wanneer u wilt weten of twee of meer variabelen statistisch onafhankelijk zijn.

Om het gedrag van een variabele te controleren, moet de test worden genoemd Chi Square -aanpassingstest. Om te weten of twee of meer variabelen statistisch onafhankelijk van de test worden genoemd Chi -plein van onafhankelijkheid, ook wel genoemd onvoorziene omstandigheden.

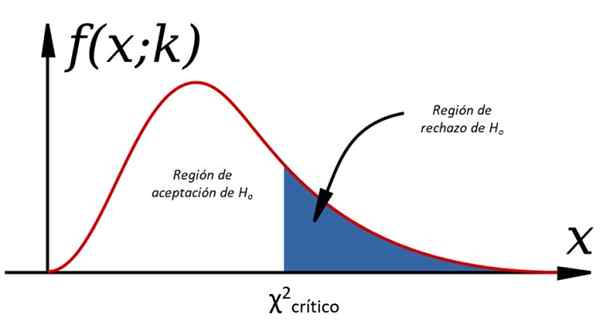
Figuur 1. Hypothesetests via Chi Cuadrado

Dit bewijs maakt deel uit van de statistische theorie van beslissingen, waarin een bevolking wordt bestudeerd en er beslissingen over worden genomen, waarbij een of meerdere monsters worden geëxtraheerd die daaruit zijn geëxtraheerd. Hiervoor is het noodzakelijk om bepaalde veronderstellingen te maken met betrekking tot de variabelen, aangeroepen hypothese, wat al dan niet zeker weet.

Er zijn enkele tests om deze vermoedens te contrasteren en te bepalen welke geldig zijn, binnen een bepaalde betrouwbaarheidsmarge, inclusief de chikwadraat-test, die kan worden toegepast om twee en de meeste populaties te vergelijken.

Zoals we zullen zien, worden meestal twee soorten hypothesen over een populatieparameter in twee monsters beschouwd: de nulhypothese, H genoemd h_of (de monsters zijn onafhankelijk), en de alternatieve hypothese, aangeduid als h₁, (de monsters zijn gecorreleerd) wat in strijd is met dat.

[TOC]

Wanneer wordt de chi-kwadraatstest gebruikt?

De Chi Square -test is van toepassing op variabelen die kwaliteiten beschrijven, zoals seks, civiele status, bloedgroep, oogkleur en voorkeuren van verschillende typen.

De test is ontworpen wanneer gewenst:

-Controleer of een verdeling geschikt is om een ​​variabele te beschrijven, die wordt genoemd aanpassing goedheid. Via de Chi Square -test kunt u weten of er significante verschillen zijn tussen de geselecteerde theoretische verdeling en de waargenomen frequentieverdeling.

-Weet of twee X- en Y -variabelen onafhankelijk zijn van het statistische standpunt. Dit staat bekend als Onafhankelijkheidstest.

Omdat het van toepassing is op kwalitatieve of categorische variabelen, wordt de Chi Square -test veel gebruikt in sociale wetenschappen, administratie en geneeskunde.

Voorwaarden om het toe te passen

Er zijn twee belangrijke vereisten om het correct toe te passen:

Het kan u van dienst zijn: wat is de relatie tussen het rhombusgebied en de rechthoek?

-De gegevens moeten in frequenties worden gegroepeerd.

-Het monster moet groot genoeg zijn om de chi -vierkante verdeling geldig te maken, anders wordt de waarde ervan overschat en geeft het aanleiding tot de afwijzing van de nulhypothese wanneer het niet zo zou moeten zijn.

De algemene regel is dat als in de gegroepeerde gegevens een frequentie met waarde van minder dan 5 verschijnt, deze niet wordt gebruikt. Als er meer dan één frequentie minder dan 5 is, moeten ze in één worden gecombineerd om een ​​frequentie te verkrijgen met numerieke waarde groter dan 5.

Chi -vierkante verdeling

χ² Het is een continue verdeling van kansen. Er zijn eigenlijk verschillende curven, afhankelijk van een parameter k genaamd graden van vrijheid willekeurig.

De eigenschappen zijn:

-Het gebied onder de curve is gelijk aan 1.

-De waarden van χ² Ze zijn positief.

-De verdeling is asymmetrisch, dat wil zeggen, het heeft vooringenomenheid.

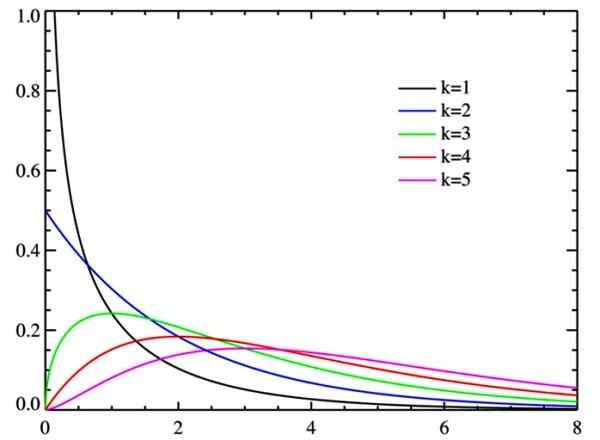Figuur 2. Chi -vierkante verdeling voor Watts -vrijheidsgraden. Bron: Wikimedia Commons.

Graden van vrijheid

Naarmate de vrijheidsgraden toenemen, neigt de chikwadraatverdeling te normaal, zoals te zien is in de figuur.

Voor een bepaalde verdeling worden de vrijheidsgraden bepaald door de rampentabel, die de tabel is waar de waargenomen frequenties van de variabelen worden opgenomen.

Als een tafel heeft F Rangen en C kolommen, de waarde van k is:

K = (F - 1) ⋅ (C - 1)

Hypotheseformulering

Wanneer de chi -vierkantstest aanpassing is, worden de volgende hypothesen geformuleerd:

-H_of: Variabele X heeft waarschijnlijkheidsverdeling F (x) met specifieke parameters en₁, En₂… , En_P

-H₁: X heeft nog een kansverdeling.

De waarschijnlijkheidsverdeling die in de nulhypothese wordt aangenomen, kan bijvoorbeeld de goed bekende normale verdeling zijn en de parameters zouden de gemiddelde μ en de standaardafwijking σ zijn.

Bovendien wordt de nulhypothese geëvalueerd met een bepaald niveau van significantie, dat wil zeggen een maat voor de fout die zou worden gemaakt bij het afwijzen van het waar.

Over het algemeen is dit niveau vastgesteld van 1 %, 5 % of 10 % en hoe lager het testresultaat, hoe betrouwbaarder.

Kan je van dienst zijn: mumm

En als de chi -vierkantstest van contingentie wordt gebruikt, die zoals we hebben gezegd, dient om de onafhankelijkheid tussen twee variabelen X en Y te verifiëren, zijn de hypothesen:

-H_of: De variabelen x en y zijn onafhankelijk.

-H₁: X en y zijn afhankelijk.

Nogmaals is het noodzakelijk om een ​​significantieniveau op te geven om de maat voor de fout te kennen bij het nemen van de beslissing.

Hoe worden chikwadraatstatistieken berekend??

Chi -vierkante statistieken worden als volgt berekend:

Het symbool ∑ betekent "sommatie", die we moeten maken over de aangegeven fractionele expressie.

De som wordt uitgevoerd van de eerste klasse I = 1 tot de laatste, dat is i = k.

Daarnaast:

-F_of Het is een waargenomen frequentie (het komt van de verkregen gegevens).

-F_En Het is de verwachte of theoretische frequentie (het is noodzakelijk om het uit de gegevens te berekenen).

Om de nulhypothese te accepteren of af te wijzen, wordt χ berekend² Voor waargenomen gegevens en vergelijkt met een waarde die wordt genoemd Chi kritisch vierkant, die afhangt van de vrijheidsgraden k en het niveau van significantie α:

χ²_kritisch =  χ²_{K, α}

Als we bijvoorbeeld de test willen uitvoeren met een significantieniveau van 1 %, dan α = 0.01, als het met 5% zal zijn, dan α = 0.05 enzovoort. P, de distributieparameter, zoals:

P = 1 - α

Deze kritische vierkante waarden worden bepaald door tabellen die de waarde van het geaccumuleerde gebied bevatten. Bijvoorbeeld, voor k = 1, die 1 graad van vrijheid vertegenwoordigt en α = 0.05, gelijkwaardig aan p = 1-.05 = 0.95, de waarde van χ² Het is 3.841.

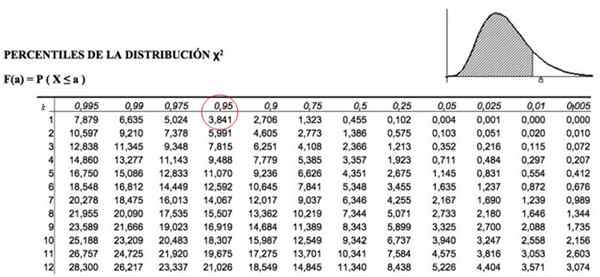figuur 3. Chi Square Distribution Values ​​Tabel. Bron: f. Zapata.

AC -acceptatiecriteria_of

De criteria om h te accepteren_of is:

-Ja χ² < χ²_kritisch  H_of, Anders wordt het afgewezen (zie figuur 1).

Voorbeeld van berekening

In de volgende toepassing wordt de Chi Square -test gebruikt als een onafhankelijkheidstest.

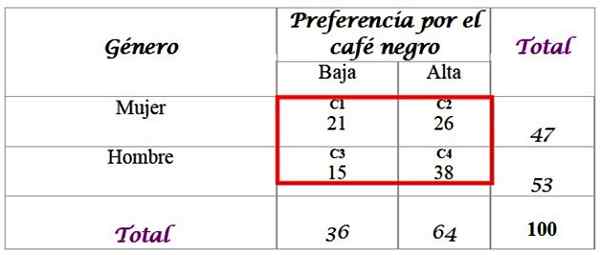
Neem aan dat onderzoekers willen weten of de voorkeur voor zwarte koffie gerelateerd is aan het genre van de persoon en het antwoord specificeren met een significantieniveau van α = 0.05.

Kan u van dienst zijn: externe alternatieve hoeken: oefeningen en oefeningen opgelost

Hiervoor zijn een voorbeeld van 100 geïnterviewde mensen en hun antwoorden beschikbaar:

Stap 1

Hypothesen vaststellen:

-H_of: Geslacht en voorkeur voor zwarte koffie zijn onafhankelijk.
-H₁: De smaak voor zwarte koffie is gerelateerd aan het genre van de persoon.

Stap 2

Bereken de verwachte frequenties voor distributie, waarvoor het totaal toegevoegd in de laatste rij en in de rechter -wing kolom vereist zijn. Elke cel in de rode doos heeft een verwachte waarde F_En, die wordt berekend door het totaal van zijn R -rij F te vermenigvuldigen met de totale kolom C, gedeeld door het totale monster N:

F_En = (F x c) /n

De resultaten zijn als volgt voor elke cel:

-C1: (36 x 47) / 100 = 16.92
-C2: (64 x 47) / 100 = 30.08
-C3: (36 x 53) / 100 = 19.08
-C4: (64 x 53) / 100 = 33.92

Stap 3

Vervolgens moet u de Chi Cuadrado -statistiek voor deze verdeling berekenen, volgens de gegeven formule:

χ²= [(21 - 16.92)² ÷ 16. 92] + [(26 - 30.08)² ÷ 30.08] + [(15 - 19.08)² ÷ 19.08]+ [(38 - 33.92)² ÷ 33. 92] = 0.9838 + 0.5534 + 0.8725 + 0.4908 = 2.9005

Stap 4

Bepaal χ²_kritisch, Wetende dat de geregistreerde gegevens zijn op F = 2 rijen en C = 2 kolommen, daarom is het aantal vrijheidsgraden:

K = (2-1) ⋅ (2-1) = 1.

Wat betekent dat we in de bovenstaande tabel moeten kijken²_{K, α} = χ²_{1; 0.05} , dat is:

χ²_kritisch = 3.841

Stap 5

Vergelijk de waarden en beslis:

χ² = 2.9005

χ²_kritisch = 3.841

Sinds χ² < χ²_kritisch De nulhypothese wordt geaccepteerd en er wordt geconcludeerd dat de voorkeur voor zwarte koffie niet is gekoppeld aan het genre van de persoon, met een significantieniveau van 5%.

Referenties

1. Chi Square -test voor onafhankelijkheid. Hersteld van: saylordotorg.Gitub.Io.
2. Med Wave. Statistieken van toepassing op gezondheidswetenschappen: de Ji-Square-test. Hersteld van: MedWave.Klet.
3. Waarschijnlijkheden en statistieken. SHI Square aanpassing goedheidstest. Opgehaald uit: waarschijnlijkheden en estics.com.
4. Triola, m. 2012. Elementaire statistieken. 11e. Editie. Addison Wesley.
5. UNAM. Chikwadraattoets. Hersteld van: advies.Cuautitlan2.UNAM.mx.