Vectorbedragen

Wat zijn vectorbedragen?

De Vectorgrootheid, of vector, als een waarvoor het nodig is om zowel de grootte als de module (met de respectieve eenheden) en hun adres te specificeren.

In tegenstelling tot de vectorhoeveelheid, heeft een scalaire hoeveelheid alleen een grootte (en eenheden), maar geen adres. Enkele voorbeelden van scalaire hoeveelheden zijn de temperatuur, het volume van een object, de lengte, de massa en de tijd, onder andere.

Verschil tussen vectorhoeveelheid en klimmen

In het volgende voorbeeld kunt u leren een scalaire hoeveelheid te onderscheiden van een vectorhoeveelheid:

Een snelheid van 10 km/u is een scalaire hoeveelheid, terwijl een snelheid van 10 km/u naar het noorden een vectorhoeveelheid is. Het verschil is dat in het tweede geval een adres is gespecificeerd, naast de grootte.

Vectorhoeveelheden hebben een oneindigheid van toepassingen, vooral in de wereld van de fysica.

Grafische afbeeldingen en denotaties van een vectorhoeveelheid

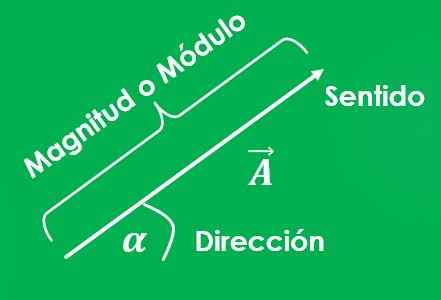
De manier om een ​​vectorbedrag aan te geven, is door een pijl (→ →) op de te gebruiken letter te plaatsen of de brief vetgedrukt te schrijven (naar)).

Om een ​​vectorhoeveelheid te verwezenlijken is een referentiesysteem nodig. In dit geval zal het Cartesiaanse vlak worden gebruikt als referentiesysteem.

De grafiek van een vector is een lijn waarvan de lengte de grootte vertegenwoordigt; en de hoek tussen genoemde lijn en de X -as, gemeten in de anti -horaire zin, vertegenwoordigt het adres.

Er moet worden gespecificeerd wat het startpunt van de vector is en wat het punt van aankomst is. Een pijl wordt ook geplaatst aan het einde van de lijn die wijst op het aankomstpunt, wat aangeeft wat de richting van de vector is.

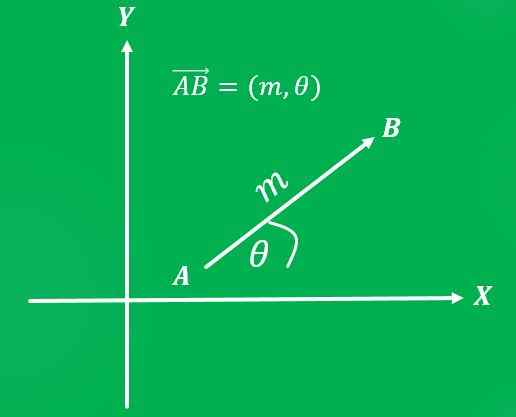
Zodra een referentiesysteem is ingesteld, kunt u de vector schrijven als een ordelijk paar: de eerste coördinaat vertegenwoordigt de grootte en de tweede coördinatie van het adres.

Voorbeelden van vectorbedragen

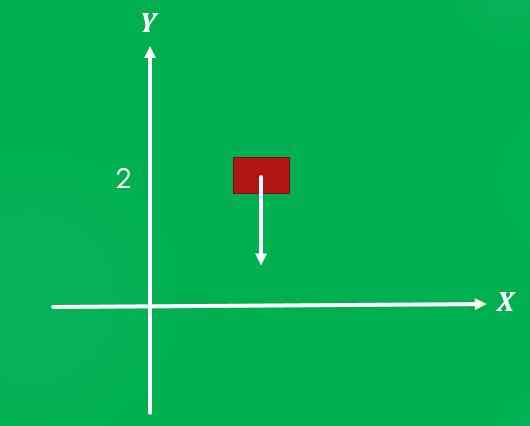
1- Zwaartekracht die op een object werkt

Als een object op een hoogte van 2 meter boven de grond wordt geplaatst en het wordt vrijgegeven, werkt de zwaartekracht erop met een grootte van 9,8 m/s² en een richting loodrecht op de grond in de richting.

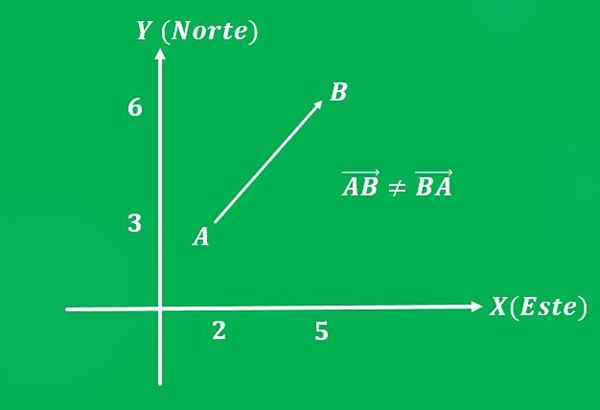
2- Beweging van een vlak

Een vlak dat van punt A = (2,3) verplaatst naar punt B = (5.6) van het Cartesiaanse vlak, met een snelheid van 650 km/u (magnitude). De richting van het traject is 45 ° ten noordoosten (betekent).

Opgemerkt moet worden dat, als de volgorde wordt omgekeerd, de vector dezelfde omvang en dezelfde richting heeft, maar verschillende betekenis, die zuidwesten zal zijn.

3- Force toegepast op een object

Juan besluit een stoel te duwen met een kracht van 10 pond, in een richting parallel aan de grond. De mogelijke zintuigen van de uitgeoefende kracht zijn: links of rechts (in het geval van het Cartesiaanse vlak).

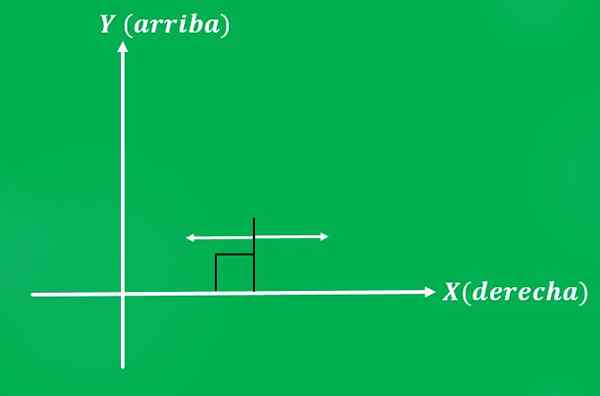
Evenals in het vorige voorbeeld, zal de betekenis die Juan besluit de kracht te geven een ander resultaat opleveren.

Dit vertelt ons dat twee vectoren dezelfde grootte en richting kunnen hebben, maar anders kunnen zijn (verschillende resultaten produceren).

Twee of meer vectoren kunnen worden toegevoegd en afgetrokken, waarvoor er zeer nuttige resultaten zijn, zoals de parallellogramwet. U kunt ook een vector vermenigvuldigen met een scalair.