Gratis conceptconcept, vergelijkingen, oefeningen opgelost

De vrije val Het is de verticale beweging die een object ervaart wanneer het van een bepaalde hoogte in de buurt van het aardoppervlak wordt gevallen. Het is een van de eenvoudigste en meest directe bewegingen die bekend zijn: in een rechte lijn en met constante versnelling.

Alle objecten die zijn gevallen, of die verticaal omhoog of omlaag worden gegooid, bewegen met de versnelling van 9.8 m/s² verstrekt door de ernst van de aarde, ongeacht de massa ervan.

Vrije val van een klif. Bron: Pexels.com.

Dit feit kan vandaag zonder problemen worden geaccepteerd. Het begrijpen van de ware aard van de vrije val duurde echter een tijdje. De Grieken hadden het al beschreven en zeer in principe geïnterpreteerd tegen de vierde eeuw a c.

[TOC]

Vergelijkingen van de vrije valbeweging

Eenmaal overtuigd dat versnelling hetzelfde is voor alle lichamen die worden vrijgegeven onder de actie van de zwaartekracht, is het tijd om de nodige vergelijkingen vast te stellen om deze beweging te verklaren.

Het is belangrijk om te benadrukken dat er in dit eerste bewegingsmodel geen rekening wordt gehouden met luchtweerstand. De resultaten van dit model zijn echter zeer nauwkeurig en dicht bij de realiteit.

In alles wat volgt zal het deeltjesmodel worden verondersteld, dat wil zeggen dat de dimensies van het object niet in aanmerking worden genomen, ervan uitgaande dat de gehele massa op één punt is geconcentreerd.

Voor een uniform versnelde rechtlijnige beweging wordt deze genomen als een referentieas naar de as en. De positieve zin wordt opgenomen en het negatieve down.

De kinematische magnitudes

Op deze manier zijn de vergelijkingen van de positie, de snelheid en de versnelling afhankelijk van de tijd:

Versnelling

A = G = -9.8 m/s² (-32 voet/s²))

Positie afhankelijk van de tijd: en (t)

y = y_of + v_of . T + ½ gt²

Waar en_of Het is de beginpositie van de mobiel en V_of is de initiële snelheid. Vergeet niet dat in de verticale lancering de beginsnelheid noodzakelijkerwijs verschilt van 0.

Dat kan worden geschreven als:

en en_of = V_of . T + ½ gt²

Δy = V_of . T + ½ gt²

Met δEn De verplaatsing zijn gemaakt door het mobiele deeltje. In eenheden van het internationale systeem worden zowel de positie als de verplaatsing gegeven in meters (M).

Snelheid afhankelijk van tijd: V (t)

v = v_of + G . T

Snelheid afhankelijk van verplaatsing

Het is mogelijk om een ​​vergelijking af te leiden die verplaatsing verbindt met snelheid, zonder tussenliggende tijd. Om dit te doen, wordt de tijd van de laatste vergelijking gewist:

Kan u van dienst zijn: kwantummechanisch model van de atoom

 En het wordt vervangen in de verplaatsingsvergelijking:

Δy = V_of . T + ½ gt²

Het vierkant is ontwikkeld met behulp van het opmerkelijke product en termen worden hergroepeerd.

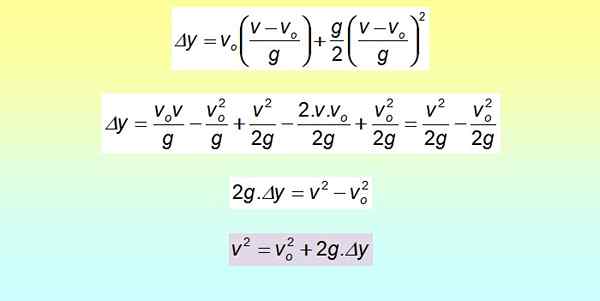
Deze vergelijking is nuttig wanneer de tijd niet beschikbaar is, maar in plaats daarvan zijn er snelheden en verplaatsingen, zoals te zien is in het gedeelte van opgeloste voorbeelden.

Voorbeelden van vrije val

De attente lezer zal de aanwezigheid van de beginsnelheid V hebben opgemerkt_of. De vorige vergelijkingen zijn geldig voor verticale bewegingen onder de werking van de zwaartekracht, beide wanneer het object van een bepaalde hoogte valt, alsof het verticaal omhoog of omlaag wordt gegooid.

Wanneer het object daalt, wordt het gewoon gedaan v_of = 0 en vergelijkingen worden als volgt vereenvoudigd.

Versnelling

A = G = -9.8 m/s² (-32 voet/s²))

Positie afhankelijk van de tijd: en (t)

y = y_of+ ½ GT²

Snelheid afhankelijk van tijd: V (t)

v = g . T

Snelheid afhankelijk van verplaatsing

v² = 2g. Dy

Dy Sindsdien zal het ook negatief zijn v² Het moet een positief bedrag zijn. Dit zal zowel gebeuren als de oorsprong of nul van het coördinatensysteem op het lanceerpunt of op de grond.

Als de lezer het de voorkeur geeft, kan hij de richting naar beneden nemen als positief. De zwaartekracht zal blijven handelen als wordt gedacht dat dat + 9 is.8 m/s². Maar u moet consistent zijn met de geselecteerde tekenconventie.

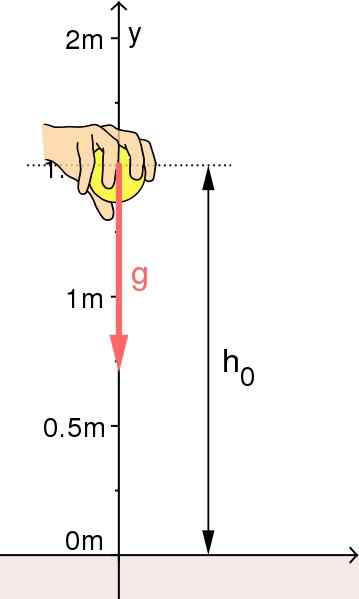Vrije val van een object: de oorsprong van het referentiesysteem is op de grond geselecteerd. Bron: Bron: Mikerun [CC BY-SA 4.0 (https: // creativeCommons.Org/licenties/by-sa/4.0)]

Verticale lancering

Hier kan de initiële snelheid natuurlijk niet nul zijn. We moeten het object bieden voor een impuls om omhoog te gaan. Volgens de initiële snelheid zal het object stijgen tot grotere of mindere hoogte.

Natuurlijk zal er een moment zijn waarop het object even stopt. Dan zal de maximale hoogte zijn bereikt met betrekking tot het lanceringspunt. Ook is de versnelling nog steeds G -down. Laten we eens kijken wat er in dit geval gebeurt.

Berekening van de maximale bereikte hoogte

Mij ​​kiezen = 0:

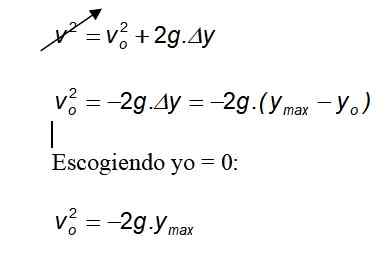
Omdat de zwaartekracht altijd in de negatieve richting naar de grond wijst, wordt het negatieve teken geannuleerd.

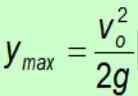
Maximale tijdberekening

Een vergelijkbare procedure dient om de tijd te vinden die het object nodig heeft om de maximale hoogte te bereiken.

v = v_of + G . T

Het doet v = 0

v_of = - g . T_Maximaal

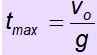
Flight Time is de tijd dat het object in de lucht duurt. Als het object terugkeert naar het startpunt, is de stijgtijd gelijk aan de afdalingstijd. Daarom is vliegtijd 2. T Max.

Kan u van dienst zijn: Microscopische schaal: eigenschappen, teldeeltjes, voorbeelden

Is twee keer de t_Maximaal De totale tijd dat het object in de lucht duurt? Ja, zolang het object vanaf een punt begint en er naar terugkeert.

Als de lancering van een bepaalde hoogte op de grond wordt gemaakt en het object hiertoe mag blijven, is de vliegtijd niet langer de maximale tijd meer.

Opgeloste oefeningen

In de resolutie van de volgende oefeningen zal het volgende worden overwogen:

1 De hoogte van waar het object wordt gevallen, is klein in vergelijking met de straal van de aarde.

2-De luchtweerstand is verachtelijk.

3 De waarde van de versnelling van de zwaartekracht is 9.8 m/s²

4-wanneer het problemen zijn met een enkele mobiel, wordt bij voorkeur gekozen en_of = 0 op het startpunt. Dit vergemakkelijkt meestal berekeningen.

5-als minder dan het tegenovergestelde is aangegeven, wordt de opwaartse richting als positief beschouwd.

6 -In de oplopende en afnemende gecombineerde bewegingen bieden de toegepaste vergelijkingen direct de juiste resultaten, zolang de consistentie wordt gehandhaafd met de tekenen: positief, neer negatief en ernst -9.8 m/s² of -10 m/s² Als u liever rondkomt (voor meer comfort bij het berekenen).

Oefening 1

Een bal wordt verticaal omhoog gegooid met een snelheid van 25.0 m/s. Beantwoord de volgende vragen:

a) Hoeveel stijgt het?

b) Hoe lang duurt het om het hoogste punt te bereiken?

c) Hoe lang duurt de bal om het aardoppervlak aan te raken nadat het zijn hoogste punt heeft bereikt?

d) Wat is uw snelheid wanneer u terugkeert naar het niveau van waar het begon?

Oplossing

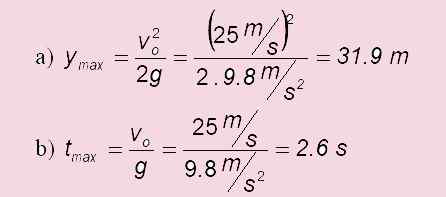
c) In het geval van een niveau -lancering: T_vlucht = 2 . T_Maximaal = 2 x6 s = 5.1 s

D) Wanneer het terugkeert naar het startpunt, heeft de snelheid dezelfde grootte als de initiële snelheid maar tegengestelde richting, daarom moet het - 25 m/s zijn. Het wordt eenvoudig gecontroleerd door waarden in de vergelijking te vervangen voor snelheid:

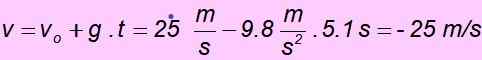
Oefening 2

Een kleine postkoffer komt vrij uit een helikopter die daalt met een constante snelheid van 1.50 m/s. Na 2.00 s Bereken:

a) Wat is de snelheid van de koffer?

b) Hoe ver is de koffer onder de helikopter?

c) Wat zijn uw antwoorden voor secties a) en b) Als de helikopter stijgt met een constante snelheid van 1.50 m/s?

Oplossing

Sectie A

Bij het verlaten van de helikopter draagt ​​de koffer de initiële snelheid ervan daarom v_of = -1.50 m/s. Met de aangegeven tijd is de snelheid toegenomen dankzij de versnelling van de zwaartekracht:

Kan u van dienst zijn: hemelse lichamen

v = v_of + G . t = -1.50 - (9.8 x 2) m/s = - 21.1 m/s

Sectie B

Laten we eens kijken hoeveel de koffer op dat moment is afgedaald ten opzichte van het startpunt:

Koffer: Dy = v_of . T + ½ gt² = -1.50 x 2 + ½ (-9.8) x 2² M = -22.6 m

Het is geselecteerd En_of = 0 Op het startpunt, zoals aangegeven aan het begin van de sectie. Het negatieve teken geeft aan dat de koffer 22 is afgedaald. 6 m onder het startpunt.

Ondertussen de helikopter Het is gevallen Snel -1.50 m/s, nemen we constant aan, daarom in de aangegeven tijd van 2 seconden, heeft de helikopter gereisd:

Helikopter: δy = v_of.t = -1.vijftig x 2 m = -3 m.

Daarom worden na 2 seconden de koffer en de helikopter gescheiden door een afstand van:

D =| -22.6 - (-3) | M = 19. 6 m.

De afstand is altijd positief. Om dit feit te benadrukken, wordt de absolute waarde gebruikt.

Sectie C

Wanneer de helikopter stijgt, heeft deze een snelheid van + 1.5 m/s. Met die snelheid komt de koffer naar buiten, zodat na 2 s al draagt:

v = v_of + G . T = +1.50 - (9.8 x 2) m/s = - 18.1 m/s

De snelheid blijkt negatief te zijn, want na 2 seconden beweegt de koffer naar beneden. Is toegenomen dankzij de zwaartekracht, maar niet zoveel als in sectie A.

Nu zullen we ontdekken hoeveel de koffer is afgedaald ten opzichte van het startpunt tijdens de eerste 2 seconden reizen:

Valija: δy = v_of . T + ½ gt² = +1.50 x 2 + ½ (-9.8) x 2² M = -16 .6 m

Ondertussen, de helikopter Het is gestegen Met betrekking tot het uitgangspunt en heeft het met constante snelheid gedaan:

Helikopter: δy = v_of.T = +1.vijftig x 2 m = +3 m.

Na 2 seconden worden een koffer en helikopter gescheiden door een afstand van:

D =| -16.6 - (+3) | M = 19.6 m

De afstand die ze scheidt, is in beide gevallen hetzelfde. De koffer reist in het tweede geval minder verticale afstand, omdat de initiële snelheid naar boven was gericht.

https: // youtu.be/w2uvetxwsfk

Referenties

1. Kirkpatrick, l. 2007. Natuurkunde: een blik op de wereld. 6^ta Afgekort editie. Cengage leren.  23 - 27.
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14^e. ED. Volume1. 50 - 53.
4. Serway, r., Vulle, c. 2011. Fundamentals of Physics. 9^NA ED. Cengage leren. 43 - 55.
5. Wilson, J. 2011. Natuurkunde 10. Pearson Education. 133 - 149.