Geconjugeerd binomiaal hoe het wordt opgelost, voorbeelden, oefeningen

A Geconjugeerd binomiaal Van een ander binomiaal is er een waarin ze alleen verschillen door een teken van de operatie. De binomiale is, zoals de naam al aangeeft, een algebraïsche structuur die uit twee termen bestaat.

Enkele voorbeelden van binomials zijn: (A + B), (3M - n) En (5x - y). En hun respectieve geconjugeerde binomials zijn: (a - b), (-3m - n) en (5x + y). Zoals onmiddellijk te zien is, zit het verschil in het teken.

Figuur 1. Een binomiaal en zijn geconjugeerde binomiaal. Ze hebben dezelfde termen, maar verschillen in het teken. Bron: f. Zapata.

Een binomiaal vermenigvuldigd met zijn conjugaat resulteert in een opmerkelijk product dat veel wordt gebruikt in algebra en wetenschap. Het resultaat van vermenigvuldiging is de aftrekking van de vierkanten van de termen van de oorspronkelijke binomiale.

Bijvoorbeeld, (X - y) Het is een binomiaal en zijn conjugaat is (x + y). Vervolgens is het product van de twee binomials het verschil van de vierkanten van de termen:

(X - y).(x + y) = x² - En²

[TOC]

Hoe wordt een geconjugeerde binomiale opgelost?

De regel die wordt uitgesproken met de geconjugeerde binomials is als volgt: 

Het product van twee geconjugeerde binomials is gelijk aan het kwadraat van de eerste termijn minus het vierkant van de tweede termijn. Dit resultaat wordt vierkant verschil genoemd.

Als een voorbeeld van de toepassing zullen we beginnen met het demonstreren van het vorige resultaat, dat kan worden gedaan met behulp van de distributieve eigenschap van het product ten opzichte van de algebraïsche som.

(x - y) (x + y) = x.x + x.en en.X - Y.En

De eerdere vermenigvuldiging werd verkregen volgens deze stappen:

- De eerste term van de eerste binomiale wordt vermenigvuldigd met de eerste termijn van de tweede

- Dan de eerste van de eerste, voor de tweede van de tweede

- Dan de tweede van de eerste voor de eerste van de tweede 

- Eindelijk de tweede van de eerste voor de tweede van de tweede.

Kan u van dienst zijn: vectoralgebra

Laten we nu een kleine wijziging aanbrengen met behulp van commutatieve eigenschap: En.x = x.En. Het blijft zo:

(x - y) (x + y) = x.x + x.y - x.en en.En

Omdat er twee gelijke termen zijn, maar anders (gemarkeerd in kleur en onderstreept), worden ze geannuleerd en vereenvoudigd:

(x - y) (x + y) = x.X - Y.En

Ten slotte wordt toegepast dat het vermenigvuldigen van een getal van zichzelf gelijk is aan het optillen van het vierkant, dus X.x = x² en ook En.y = y².

Op deze manier, wat in de voorgaande sectie was opgemerkt, is het product van een verschil het verschil van de vierkanten:

(X - y).(x + y) = x² - En²

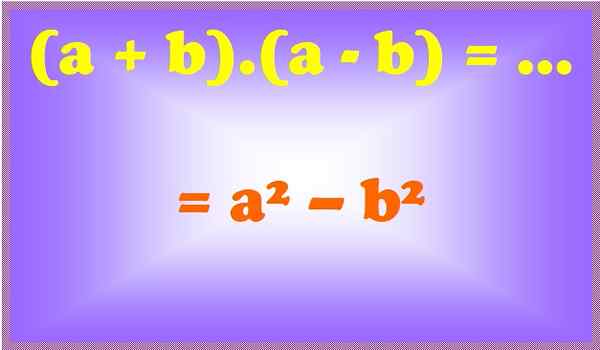Figuur 2. Een som voor het verschil is een verschil van vierkanten. Bron: f. Zapata.

Voorbeelden

- Geconjugeerde binomials van verschillende uitdrukkingen

voorbeeld 1

Vind het conjugaat van (en² - 3y).

Antwoord: (En² + 3y)

Voorbeeld 2

Krijg het product van (en² - 3y) voor zijn conjugaat.

Antwoord: (En² - 3y) (en² + 3y) = (en²))² - (3Y)² = Y⁴ - 3² En² = Y⁴ - 9y²

Voorbeeld 3

Ontwikkel het product (1 + 2a).(2a -1).

Antwoord: De vorige uitdrukking is equivalent aan (2a + 1).(2a -1), dat wil zeggen, het komt overeen met het product van een binomiaal voor zijn conjugaat.

Het is bekend dat het product van een binomiaal voor zijn geconjugeerde binomiaal gelijk is aan het verschil van de vierkanten van de binomiale termen:

(2a + 1) (2a -1) = (2a)² - 1² = 4 a² - 1

Voorbeeld 4

Schrijf het product (x + y + z) (x - y - z) als een verschil van vierkanten.

Antwoord: We kunnen de trinomials assimileren voorafgaand aan de vorm van geconjugeerde binomials, zorgvuldig gebruik van haakjes en vierkante beugels:

(x + y + z) (x - y - z) = [x + (y + z)] [x - (y + z)]

Op deze manier kan het verschil tussen vierkanten worden toegepast:

(x + y + z) (x - y - z) = [x + (y + z)].[x - (y+z)] = x² - (Y+z)²

Voorbeeld 5

Druk het product uit (m² - m -1).(M² + m -1) als een verschil in vierkanten.

Kan u van dienst zijn: 120 delers

Antwoord: De vorige uitdrukking is het product van twee trinomials. Ten eerste moet het worden herschreven als het product van twee geconjugeerde binomials:

(M² - m -1) (m² + m -1) = (m² - 1 - m) (m² -1 + m) = [(m² -1) - m].[(M² -1) +m)]

We passen het feit toe dat het product van een binomiaal door zijn conjugaat het kwadratische verschil van zijn termen is, zoals uitgelegd:

[(M² -1) - m].[(M² -1) +m)] = (m² -1)² - M²

Opdrachten

Zoals altijd begint het met de eenvoudigste oefeningen en dan verhoogt het niveau van complexiteit.

- Oefening 1

ESCRIBA (9 - A²) als een product.

Oplossing

Ten eerste herschrijven we de uitdrukking als een verschil van vierkanten, om toe te passen wat eerder uitlegde. Daarom:

(9 - A²) = (3² - naar²))

We factoren onmiddellijk, wat gelijk is aan het schrijven van dit verschil van vierkanten als een product, zoals gevraagd in de verklaring:

(9 - A²) = (3² - naar²) = (3 + a) (3 -A)

- Oefening 2

Factorize 16x² - 9y⁴.

Oplossing

Factor Een uitdrukking betekent het schrijven als een product. In dit geval is het noodzakelijk om de uitdrukking eerder te herschrijven om een ​​verschil van vierkanten te verkrijgen.

Het is niet moeilijk om het te doen, omdat het zorgvuldig observeren, alle factoren zijn perfecte vierkanten. Bijvoorbeeld 16 is het kwadraat van 4, 9 is het kwadraat van 3, En⁴ is het kwadraat van En² En X² is het kwadraat van X:

16x² - 9y⁴  = 4²X² - 3²En⁴ = 4²X²  - 3²(En²))²

Wat we dan al weten, wordt toegepast: dat een verschil in vierkanten het product is van geconjugeerde binomials:

(4x)² - (3 en²))² = (4x - 3 en²)) . (4x + 3 en²))

- Oefening 3

Schrijf (a - b) als een binomiaal product

Oplossing

Het vorige verschil moet worden geschreven als vierkante verschillen

(√a)² -(√B)²

Dan wordt toegepast dat het verschil in vierkanten het product is van de geconjugeerde binomials

Kan u van dienst zijn: vermindering van vergelijkbare termen

(√a - √b) (√a + √b)

- Oefening 4

Een van de toepassingen van het geconjugeerde binomiale is de rationalisatie van algebraïsche uitdrukkingen. Deze procedure bestaat uit het elimineren van de wortels van de noemer van een fractionele uitdrukking, die bij verschillende gelegenheden de bewerkingen vergemakkelijkt. Er wordt gevraagd om de geconjugeerde binomiale te gebruiken om de volgende uitdrukking te rationaliseren:

√ (2 -x) / [√3 - √ (2+x)]]

Oplossing

De eerste is om de geconjugeerde binomiale van de noemer te identificeren: [√3 + √ (2 + x)]].

Nu vermenigvuldigen we de teller en noemer van de oorspronkelijke uitdrukking door de geconjugeerde binomiale:

√ (2 -x) [√3+√ (2+x)] /[√3 - √ (2+x)].[√3 + √ (2 + x)]

In de noemer van de vorige uitdrukking herkennen we het product van een verschil door een som, waarvan we al weten dat het overeenkomt met het verschil van de vierkanten van de binomials:

√ (2-X) .[√3 + √ (2 + x)] /(√3)² - [√ (2+x)]² 

Het vereenvoudigen van de noemer is:

√ (2-X).[√3+√ (2+x)] / [3 - (2+x)] = √ (2 -x). [√3 + √ (2 + x)] / (1 - x)

Nu zorgen we voor de teller, waarvoor we de distributieve eigenschap van het product met betrekking tot de som zullen toepassen:

√ (2-X) .[√3 + √ (2 + x)] / (1 - x) = √ (6-3x) + √ [(2 -x) (2 + x)] / (1 - x)

In de vorige uitdrukking herkennen we het product van het binomiale (2-X) voor zijn conjugaat, dat het opmerkelijke product is dat gelijk is aan het verschil van vierkanten. Op deze manier wordt uiteindelijk een gerationaliseerde en vereenvoudigde uitdrukking verkregen:

[√ (6-3x) + √ (4-x²)] / (1 - x)

- Oefening 5

Ontwikkel het volgende product, met behulp van de eigenschappen van de geconjugeerde binomiale:

[2e^{(x + 3y)} - 3e^{(x - 3y)}].[2e^{(x + 3y)} + 3e^{(x - 3y)}]

Oplossing

4e^{(2x + 6y)} - 9e^{(2x - 6y)} = 4a^(2x) .naar^(6y) - 9e^(2x) .naar^(-6y)= [4a^(6y) - 9e^(-6y)] .naar^(2x)

De attente lezer zal de gemeenschappelijke factor hebben opgemerkt die in kleur is benadrukt.

Referenties

1. Baldor, een. 1991. Algebra. Venezolaanse culturele redactionele s.NAAR.
2. González J. Geconjugeerde binomiale oefeningen. Hersteld van: Academie.Edu.
3. Wiskunde Alex. Opmerkelijke producten. Hersteld van YouTube.com.
4. MATH2ME. Geconjugeerde binomials/ opmerkelijke producten. Hersteld van YouTube.com.
5. Geconjugeerde binomiale producten. Hersteld van: lms.Colbachenlinea.mx.
6. Vatbaar. Geconjugeerde binomials. Hersteld van: YouTube.com.