Ortonormale basiseigenschappen, voorbeelden en oefeningen

A Ortonormale basis Het wordt gevormd met loodrechte vectoren met elkaar en waarvan de module ook 1 waard is (eenheidsvectoren). Onthoud dat een basis B in een vectorruimte V, Het wordt gedefinieerd als een set lineair onafhankelijke vectoren die deze ruimte kunnen genereren.

Op zijn beurt is een vectorruimte een abstracte wiskundige entiteit tussen wiens elementen vectoren zijn, in het algemeen geassocieerd met fysieke magnitudes zoals snelheid, sterkte en verplaatsing of ook met matrices, polynomen en functies.

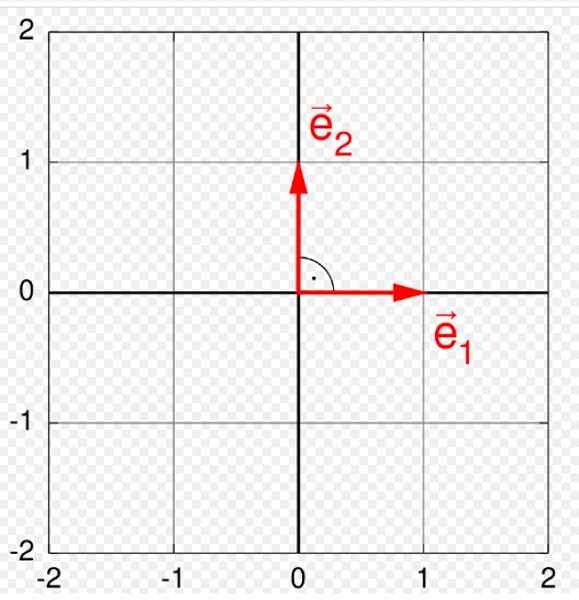
Figuur 1. Orthonormale basis in het vlak. Bron: Wikimedia Commons. Quartl [cc by-sa (https: // creativeCommons.Org/licenties/by-sa/3.0)].

Vectoren hebben drie onderscheidende elementen: magnitude of module, richting en betekenis. Een ortonormale basis is vooral handig om ermee te vertegenwoordigen en te werken, omdat elke vector die tot een bepaalde vectorruimte hoort V, Het kan worden geschreven als een lineaire combinatie van de vectoren die de ortonormale basis vormen.

Op deze manier worden bewerkingen tussen vectoren, zoals som, aftrekking en de verschillende soorten producten die in genoemde ruimte zijn gedefinieerd analyseerd analyseerd.

Een van de meest gebruikte bases van de natuurkunde is de basis gevormd door eenheidsvectoren Je, J En k De drie onderscheidende richtingen van drie -dimensionale ruimte weergeven: hoge, brede en diepte. Deze vectoren zijn ook bekend onder de naam van Unitaire canonieke vectoren.

Als in plaats daarvan vectoren op een vliegtuig worden gewerkt, zou het voldoende zijn met twee van deze drie componenten, terwijl slechts één.

[TOC]

Bases -eigenschappen

1- Een basis B Het is de kleinst mogelijke set vectoren die de vectorruimte genereren V.

2- De elementen van B Ze zijn lineair onafhankelijk.

3- Elke basis B van een vectorruimte V, maakt het mogelijk om alle vectoren uit te drukken V Als een lineaire combinatie ervan en deze vorm is uniek voor elke vector. Daarom a B Het staat ook bekend als Generatorsysteem.

4- Dezelfde vectorruimte V kan verschillende bases hebben.

Kan u van dienst zijn: centrifugale kracht: formules, hoe het wordt berekend, voorbeelden, oefeningen

Voorbeelden van bases

Onder verschillende voorbeelden van orthonormale bases en bases in het algemeen:

De canonieke basis in ℜ ^N

Ook wel een natuurlijke basis of standaardbasis van ℜ genoemd ^N, Waar ℜ ^N Het is ruimte dimensionaal, Drie -dimensionale ruimte is bijvoorbeeld ℜ ³. De waarde van N Het heet dimensie van de vectorruimte en geeft aan als Dim (v).

Alle vectoren die tot ℜ behoren ^N Ze worden vertegenwoordigd door N-USA Besteld. Voor ruimte ℜ^N, De canonieke basis is:

En₁ =; En₂ =; En_N =

In dit voorbeeld hebben we de notatie met beugels of "beugels" gebruikt en vetgedrukt voor eenheidsvectoren En₁, En₂, En₃..

De canonieke basis in ℜ³

Familievectoren Je, J En k Ze geven dezelfde weergave toe en ze zijn genoeg voor drie om de vectoren in ℜ te vertegenwoordigen ³:

Je =; J =;  k =

Het betekent dat de basis als volgt kan worden uitgedrukt:

B = ; ;

Om te controleren of ze lineair onafhankelijk zijn, is de determinant gevormde met hen vectoren niet -nul en ook gelijk aan 1:

Het moet ook mogelijk zijn om elke vector te schrijven die bij ℜ hoort ³ Als een lineaire combinatie ervan. Bijvoorbeeld een kracht waarvan de rechthoekige componenten f zijn_X = 4 n, f_En = -7 N en F_Z= 0 n zou als volgt in een vectorvorm worden geschreven:

F = N = 4Je -7J + 0k N.

Daarom Je, J En k maak een ℜ -generatorsysteem ³.

Andere ortonormale bases in ℜ³

De standaardbasis beschreven in de vorige sectie is niet de enige ortonormale basis in ℜ³. Hier hebben we bijvoorbeeld de bases:

B₁ = ;; ;

B₂ = ;; ;

Het kan worden aangetoond dat deze bases orthonormaal zijn, hiervoor herinneren we ons de voorwaarden waaraan moet worden voldaan:

Kan u van dienst zijn: golvende optica

-Vectoren die de basis vormen, moeten orthogonaal voor elkaar zijn.

-Elk van hen moet eenheid zijn.

We kunnen het verifiëren, wetende dat de door hen gevormde determinant niet moet zijn en gelijk aan 1.

Basis B₁ Het is precies dat van cilindrische coördinaten ρ, φ en z, een andere manier om vectoren in de ruimte uit te drukken.

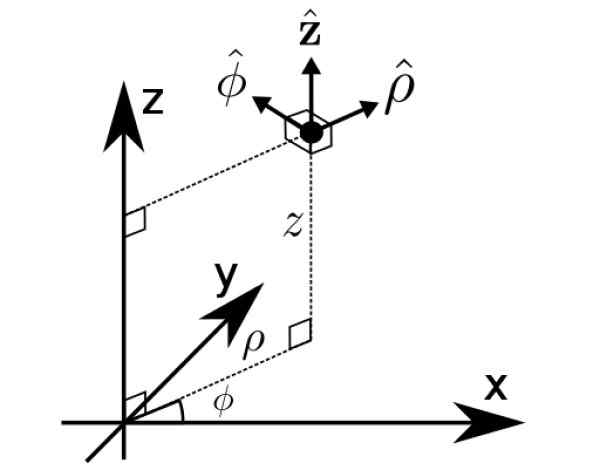Figuur 2. Cilindrische coördinaten. Bron: Wikimedia Commons. Math Buff [CC BY-S (https: // creativeCommons.Org/licenties/by-sa/4.0)].

Opgeloste oefeningen

- Oefening 1

Laat zien dat de basis B = ; ; is ortonormaal.

Oplossing

Om aan te tonen dat de vectoren loodrecht op elkaar staan, zullen we het scalaire product gebruiken, ook wel intern of productpunt van twee vectoren genoemd.

Laat twee vectoren of En v, Uw scalaire product wordt gedefinieerd door:

of • v = of.v. cosθ

Om de vectoren van hun modules te onderscheiden, zullen we vetgedrukt gebruiken voor de eerste en normale letters voor de laatste. θ is de hoek tussen of En v, Daarom als ze loodrecht zijn, betekent dit dat θ = 90º en het scalaire product nietig is.

Als alternatief, als de vectoren worden gegeven in termen van hun componenten: of = X, of_En,of_Z > En v = X, v_En,v_Z >, het scalaire product van beide, dat commutatief is, wordt op deze manier berekend:

of • v = of_X .v_X + of_En .v_En + of_Z .v_Z

Op deze manier zijn de scalaire producten tussen elk paar vectoren respectievelijk:

i) • = (3/5).(-4/5) + (4/5).((3/5) + 0.0 = (-12/25) + (12/25) = 0

Ii) • = 0

iii) • = 0

Voor de tweede voorwaarde wordt de module van elke vector berekend, die wordt verkregen door:

│u │ = √ (u_X² + of_En² + of_Z²))

De modules van elke vector zijn dus:

│ = √ [(3/5)² + (4/5)²  + 0²)] = √ [(9/25) + (16/25)] = √ (25/25) = 1

│ = √ [(-4/5)² + (3/5)²  + 0²)] = √ [(16/25) + (9/25)] = √ (25/25) = 1

Het kan u van dienst zijn: tweede evenwichtstoestand: uitleg, voorbeelden, oefeningen

│ = √ [0² + 0²  + 1²)] = 1

Daarom zijn de drie eenheidsvectoren. Ten slotte is de bepalende factor die ze vormen niet nul en gelijk aan 1:

- Oefening 2

Schrijf de vectorcoördinaten W = In termen van de vorige basis.

Oplossing

Om dit te doen wordt de volgende stelling gebruikt:

Laat B = v₁, v₂, v₃,.. v_N Een orthonormale basis in Space V met huiselijk product, de vector W Het wordt als volgt weergegeven door B:

W = <W•v₁> v₁ + <W•v₂> v₂ +<W•v₃> v₃ +.. <W•v_N> v_N

Dit betekent dat we de vector op basis B kunnen schrijven, via coëfficiënten <W•v₁>, <W•v₂>, ..  <W•v_N>, waarvoor u de aangegeven scalars moet berekenen:

• = (2).(3/5) + (3).(4/5) + 1.0 = (6/5) + (12/5) = 18/5

• = (2).(-4/5) + (3).(3/5) + 1.0 = (-8/5) + (9/5) = 1/5

• = 1

Met de verkregen scalaire producten wordt een matrix gebouwd, genaamd coördinaatmatrix van W.

Daarom coördineert de vector W In basis B worden ze uitgedrukt door:

[[W]_B= [[((18/5); ((1/5); 1]

De coördinaatmatrix is ​​niet de vector, omdat een vector niet hetzelfde is als zijn coördinaten. Dit zijn slechts een reeks getallen die dienen om de vector op een bepaalde basis uit te drukken, niet de vector als zodanig. Ze zijn ook afhankelijk van de geselecteerde basis.

Ten slotte, na de stelling, de vector W zou als volgt worden uitgedrukt:

W = (18/5) v₁ + (1/5) v₂ + v₃

Met: v₁ =; v₂ =; v₃ =, Dat wil zeggen de basisvectoren B.

Referenties

1. Larson, r. Fundamentals van lineaire algebra. 6e. Editie. Cengage leren.
2. Larson, r. 2006. Berekening. 7e. Editie. Deel 2. McGraw Hill.
3. Salas, J. lineaire algebra. Onderwerp 10. Ortonormale bases. Hersteld van: ocw.UC3M.is.
4. Sevilla University. Cilindrische coördinaten. Vectorbasis. Hersteld van: laplace.ons.is.
5. Wikipedia. Ortonormale basis. Hersteld van: is.Wikipedia.borg.