Gelijkenbare toepassingen in het dagelijks leven

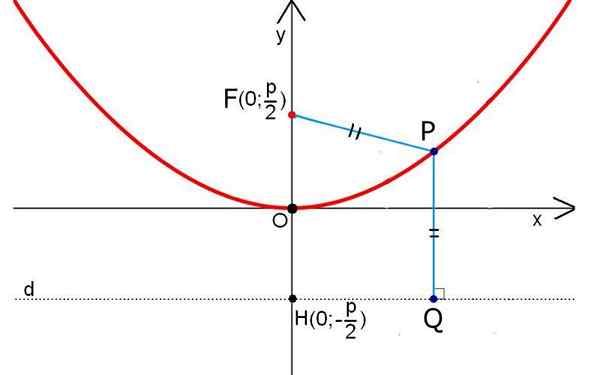
Een eenvoudige gelijkenis. Bron: Ezechië, Wikimedia Commons

De Gelijkenbare toepassingen in het dagelijks leven Ze zijn meerdere. Van de satelliet- en radiolescopesantennes om de signalen te concentreren, naar de autokoplampen bij het verzenden van parallelle lichtstralen.

Een gelijkenis, in eenvoudige bewoordingen, kan worden gedefinieerd als een curve waarin de punten op gelijke afstand zijn van een vast punt en een lijn. Het vaste punt wordt focus genoemd en de lijn staat bekend als richtlijn.

De gelijkenis is een conisch dat wordt getekend in verschillende fenomenen, zoals de beweging van een bal aangedreven door een basketbalspeler of als de waterval van een fontein.

De gelijkenis is vooral belangrijk op verschillende natuurgebieden, in weerstand van materialen of in mechanica. In de basis van mechanica en fysica worden de eigenschappen van de parabool gebruikt.

Gelijkenbare toepassingen in het dagelijks leven

Parabolische antennes

De gelijkenis kan worden gedefinieerd als een curve die zich voordoet bij het maken van een snit naar een kegel. Als deze definitie van toepassing is op een drie -dimensionaal object, zouden we een oppervlak verkrijgen dat paraboloid wordt genoemd.

Dit cijfer is erg handig vanwege een eigenschap die de gelijkenissen hebben, waarbij een punt erin op een lijn loopt parallel aan de as, "zal stuiteren" in de parabool en naar de focus worden gestuurd.

Een paraboloïde met een signaalontvanger in de focus kan alle signalen die stuiteren in de paraboloïde naar de ontvanger maken, zonder rechtstreeks naar hetzelfde te leiden. Een grote signaalreceptie wordt verkregen met behulp van de gehele paraboloïde.

Kan u van dienst zijn: de 9 principes van menselijke communicatie

Dit soort antennes worden gekenmerkt door een parabolische reflector te hebben. Het oppervlak is een paraboloïde van revolutie.

De vorm is te wijten aan een eigenschap van wiskundige gelijkenissen. Ze kunnen zenders, ontvangers of volledige duplex zijn. Ze worden op die manier genoemd wanneer ze tegelijkertijd in staat zijn om te verzenden en te ontvangen. Ze worden meestal gebruikt bij hoge frequenties.

Satellieten

Een satelliet stuurt informatie naar de aarde. Deze stralen staan ​​loodrecht op de richtlijn voor de afstand waarop de satelliet zich bevindt.

Wanneer weerspiegeld in het antenne -gerecht, dat over het algemeen wit is, convergeren de stralen in de focus, waarbij een ontvanger wordt gevonden die de informatie decodeert.

Waterstralen

Waterstralen die een leverancier verlaten, hebben een parabolische vorm.

Wanneer talloze jets uit een punt met gelijke snelheid naar voren komen, maar met verschillende neiging, staat een andere gelijkenis genaamd "beveiligingsleven" boven de andere en het is niet mogelijk dat een andere van de resterende gelijkenissen eroverheen.

Zonnekeukens

Met de eigenschap die de gelijkenissen karakteriseert, kunnen ze worden gebruikt om apparaten zoals zonnekeukens te maken.

Met een paraboloïde die de zonnestralen weerspiegelt, zou wat wordt gekookt gemakkelijk worden geplaatst, waardoor het snel heet is.

Andere toepassingen zijn de accumulatie van zonne -energie met behulp van een accumulator op de focus.

Voertuigkoplampen en parabolische microfoons

De eerder uitgelegde eigenschap van de gelijkenissen kan omgekeerd worden gebruikt. Door een signaalemitter in de richting van het oppervlak te plaatsen, zullen alle signalen in hetzelfde stuiteren in de focus van een paraboloïde. Op deze manier zal de as parallel worden weerspiegeld, waardoor een hoger niveau van signaalemissie wordt verkregen.

Het kan je van dienst zijn: 8 tradities en gewoonten van Nayarit

In de koplampen van het voertuig vindt dit plaats wanneer een lamp in de focus wordt geplaatst om meer licht uit te stoten.

In parabolische microfoons treedt het op wanneer een microfoon wordt geplaatst in de focus van een paraboloïde om meer goede hoeveelheid uit te stoten.

Hangende bruggen

De opgehangen brugkabels nemen de parabolische vorm aan. Deze vormen de envelop van een gelijkenis.

In de analyse van de balanceringscurve van de kabels, wordt toegegeven dat ze talloze riemen zijn en kan worden overwogen dat de belasting uniform horizontaal verdeeld is.

Met deze beschrijving wordt aangetoond dat de evenwichtscurve van elke kabel een eenvoudige vergelijkingspersoon is en het gebruik ervan frequent is in de techniek.

Als voorbeelden van het echte leven zijn de San Francisco Bridge (Verenigde Staten) of de Barqueta Bridge (Sevilla), die parabolische structuren gebruiken om de brug meer stabiliteit te geven.

Hemelse objecten

Er zijn periodieke kometen die langwerpige trajecten of ellipsen hebben. Wanneer de terugkeer van kometen rond het zonnestelsel niet wordt aangetoond, lijken ze een gelijkenis te beschrijven.

Sport

In elke sport waarin een lancering wordt gemaakt, vinden we gelijkenissen. Deze kunnen worden beschreven door ballen of door artefacten gegooid zoals voetbal, basketbal of speerlancering.

Deze lancering staat bekend als "parabolische lancering" en bestaat uit het ophalen van een object (niet verticaal) een object. Het pad dat het object maakt bij het stijgen (met de kracht die van toepassing is) en te verlagen (door zwaartekracht) vormt een parabool.

Een meer concreet voorbeeld zijn de toneelstukken gemaakt door Michael Jordan, NBA Basketball Player.

Kan u dienen: wat betekent sinaloa?

Deze speler is onder andere beroemd geworden voor zijn "vluchten" naar de mand, waar hij op het eerste gezicht veel langer in de lucht leek te zijn geschorst dan andere spelers.

Michael's Secret was dat hij wist hoe hij voldoende lichaamsbewegingen en een geweldige initiële Veloc moest gebruiken.

Bliksem

Wanneer een conische vormstraal op een muur wordt geprojecteerd, worden parabolische vormen verkregen, zolang de muur parallel is aan de kegel generatrix.

Referenties

1. Arnheim, C. (2015). Wiskundige oppervlakken. Duitsland: Bod
2. Boyer, c. (2012). Geschiedenis van analytische geometrie. VS: COUER CORPORATION.
3. Frankrijk, Ronald L. (1980). Een parabolische antenne met zeer lage sidelobes. IEEE transacties op antennes en verspreiding. 
4. Ketenik, D. (2002). Problemen in analytische geometrie. Hawaii: The Minerva Group.
5. Kraus, J.D. (1988). Antennes, VS: McGraw - Hill.