Factoriële rig definitie, formules en oefeningen

Hij Factoriële rig Het is een eenvoudige machine die bestaat uit een randopstelling met een vermenigvuldigingseffect van kracht. Op deze manier kunt u een lading verhogen die alleen het equivalent van een fractie van het gewicht op het vrije uiteinde van het touw aanbrengt.

Het bestaat uit twee sets katrollen: een die is vastgesteld op een ondersteuning en een andere die de resulterende kracht op de belasting uitoefent. De katrollen zijn gemonteerd op een over het algemeen metaalframe dat ze vasthoudt. 

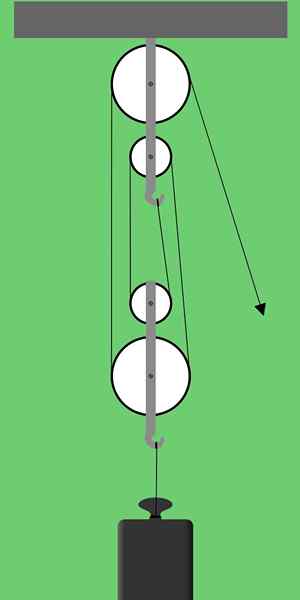
Figuur 1. Schema van een factor rig. Bron: Pixabay

Figuur 1 toont een faculteit die bestaat uit twee groepen van twee katrollen elk. Dit type poelie -arrangementen worden ook genoemd Serie rig of Polypasten.

[TOC]

Factoriële juiste formules

Case 1: een mobiele katrol en een vaste

Om te begrijpen waarom deze opstelling de uitgeoefende kracht vermenigvuldigt, zullen we beginnen met het eenvoudigste geval, bestaande uit een vaste en een mobiele poelie.

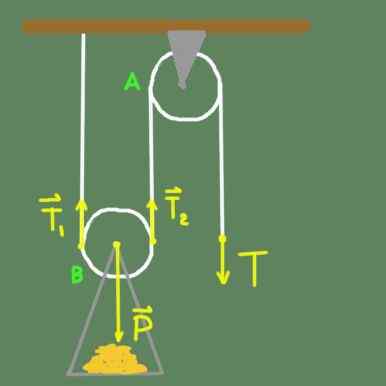Figuur 2. Twee poelie -rig.

In figuur 2 hebben we een vaste poelie naar het dak door ondersteuning. Poelie A kan vrij rond de as draaien. We hebben ook een B -poelie die een vaste ondersteuning heeft voor de poelieas, waarin de belasting is geplaatst. Poelie B heeft, naast het vrij kunnen draaien van vrij rond de as, de mogelijkheid om verticaal te bewegen.

Stel dat we zich in een evenwichtssituatie bevinden. Overweeg de krachten die op de B -poelie handelen. De B ​​-Pulley -as ondersteunt een totaal gewicht P dat naar beneden wordt gericht. Als dit de enige kracht op de B -poelie was, maar we weten dat het touw dat door deze poelie gaat ook twee krachten uitoefent, die de T1 en T2 zijn die naar boven gericht zijn.

Om te translationeel evenwicht moeten de twee krachten omhoog zijn als het gewicht dat de poelie B -as ondersteunt.

T1 + T2 = P

Maar omdat poelie B ook in rotatie -evenwicht is, dan T1 = T2. T1- en T2 -krachten komen uit de spanning die op het touw wordt uitgeoefend, T genoemd.

Het kan u van dienst zijn: Bohr Atomic Model

Daarom T1 = T2 = T. Vervangen in de vorige vergelijking blijft bestaan:

T + t = p

2t = P

Wat aangeeft dat de spanning die op het touw wordt toegepast, slechts de helft van het gewicht is:

T = p/2

Als de belasting bijvoorbeeld 100 kg was, zou dit voldoende zijn om een ​​kracht van 50 kg aan het vrije uiteinde van het touw aan te brengen om de belasting op constante snelheid te verhogen.

Case 2: Twee mobiele en twee vaste katrollen

Laten we eens kijken naar de spanningen en krachten die handelen op een set die bestaat uit twee steunen van steunen A en B met elk twee katrollen elk.

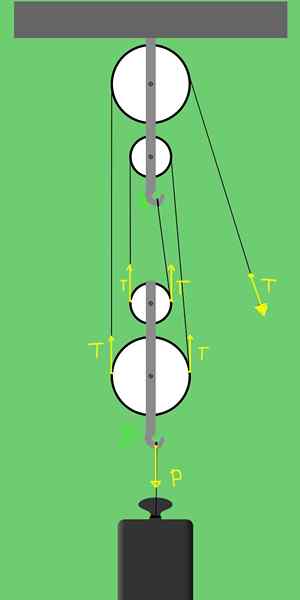figuur 3. Krachten op een rig van 2 vaste katrollen en 2 mobiele katrollen.

Ondersteuning B heeft de mogelijkheid om verticaal te bewegen, en de krachten die op de zoon handelen:

- Het gewicht p van de belasting, die verticaal naar beneden wijst.

- Twee spanningen op de grote poelie en twee spanningen op de kleine poelie. In totaal wijzen vier spanningen, allemaal wijzen ze op.

Om er een translationeel evenwicht te zijn, is het noodzakelijk dat de krachten die verticaal omhoog wijzen gelijk aan de belasting die naar beneden wijst. Dat wil zeggen, het moet worden vervuld:

T + t + t + t = p

Dat wil zeggen 4 t = p

Van waaruit volgt dat de uitgeoefende kracht T aan het vrije uiteinde van het touw slechts een kwart van het gewicht is vanwege de belasting die wil stijgen., T = p / 4.

Met deze waarde voor T -spanning kan de belasting statisch worden gehandhaafd of met constante snelheid worden gestegen. Als een grotere spanning zou worden toegepast dan deze waarde, zou de belasting versnellen, een voorwaarde die nodig is om deze uit de rest te verwijderen.

Algemeen geval: N Mobiele katrollen en N vaste katrollen

Zoals te zien in de vorige gevallen, zijn er voor elke poelie van de mobiele set een paar krachten omhoog door het touw dat door de poelie gaat. Maar deze kracht kan niets anders zijn dan de spanning die op het touw wordt uitgeoefend aan het vrije einde.

Dus voor elke mobiele set poelie is er een opwaartse kracht die 2T waard is. Maar aangezien er een katrollen in de mobiele set zijn, is het dan nodig om verticaal naar boven te wijzen, is:

Kan u van dienst zijn: eekhoornkooi -motor

2 n t

Voor verticaal evenwicht is het noodzakelijk dat:

2 n t = p

Daarom is de kracht die aan het vrije einde wordt uitgeoefend:

T = p / (2 n)

In dit geval kan worden gezegd dat de kracht uitgeoefend met t vermenigvuldigt 2 n keer op de belasting.

Als we bijvoorbeeld een factor rig hadden van 3 vaste katrollen en 3 mobiele telefoons, zou nummer N gelijk zijn aan 3. Aan de andere kant, als de belasting p = 120 kg was, zou de kracht die aan het vrije uiteinde werd uitgeoefend t = 120 kg / (2*3) = 20 kg zijn.

Opgeloste oefeningen

Oefening 1

Overweeg een factor rig bestaande uit twee vaste katrollen en twee mobiele katrollen. De maximale spanning die het touw kan ondersteunen is 60 kg. Bepaal wat de maximale belasting is die kan worden geplaatst.

Oplossing

Wanneer de belasting in rust is of constant het gewicht p daarvan beweegt, is deze gerelateerd aan de spanning T die in het touw wordt toegepast door middel van de volgende relatie:

P = 2 N T

Omdat het een rig is van twee mobiele en twee vaste katrollen, dan n = 2.

De maximale belasting die kan worden geplaatst, wordt verkregen wanneer t de maximale mogelijke waarde heeft, die in dit geval 60 kg is.

Maximale belasting = 2*2*60 kg = 240 kg

Oefening 2

Vind de relatie tussen de spanning van het touw en het gewicht van de belasting, in een factor rig van twee katrollen waarin de belasting versnelt met versnelling tot.

Oplossing

Het verschil in dit voorbeeld met betrekking tot wat tot nu toe is gezien, is dat de dynamiek van het systeem moet worden overwogen. Dus we stellen de tweede wet van Newton voor om de gevraagde relatie te vinden.

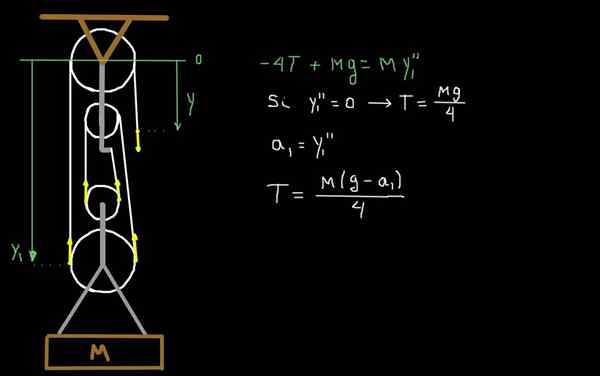Figuur 4. Dynamiek van de faculteit Rig.

In figuur 4 trekken we de krachten vanwege de spanning T van het touw. Het mobiele deel van de rig heeft een totale massa m. We nemen als referentiesysteem één op het niveau van de eerste vaste en positieve katrol naar beneden.

Y1 is de laagste positie van de katrolas.

We passen de tweede wet van Newton toe om de A1 -versnelling van het mobiele deel van de rig te bepalen:

Kan u van dienst zijn: Varignon Stelling

-4 t + mg = m a1

Omdat het gewicht van de belasting p = mg is, waarbij g de versnelling van de zwaartekracht is, kan de vorige relatie worden geschreven:

-4t + p = p (a1 / g)

Als we de spanning in het touw willen bepalen wanneer een bepaalde gewichtsbelasting wordt versneld met versnelling A1, dan zou de vorige relatie zo zijn:

T = p (1 - a1 / g) / 4

Merk op dat als het systeem in rust was of constant bewoog, dan A1 = 0, en we dezelfde uitdrukking hebben hersteld die we in geval 2 hebben verkregen.

Oefening 3

In dit voorbeeld wordt dezelfde rig van oefening 1 gebruikt, met hetzelfde touw dat maximaal 60 kg spanning ondersteunt. Een bepaalde belasting stijgt en versnelt deze van rust tot 1 m/s met 0,5 s, met behulp van de maximale spanning van het touw. Zoek het maximale belastingsgewicht.

Oplossing

We zullen de uitdrukkingen gebruiken die zijn verkregen in Oefening 2 en het referentiesysteem in figuur 4 waarin het positieve adres verticaal is.

De versnelling van de belasting is a1 = (-1 m/s -0 m/s) /0,5 s = -2 m/s^2.

Het gewicht van de belasting in kilogram-kracht wordt gegeven door

P = 4 t / (1 - a1 / g)

P = 4*60 kg / (1 + 2/9.8) = 199,3 kg

Dit is het maximaal mogelijke gewicht van de belasting zonder dat het touw wordt gebroken. Merk op dat de verkregen waarde minder is dan die verkregen in Voorbeeld 1, waarin de belasting werd verondersteld met nulversnelling, dat wil zeggen in rust of constante snelheid.

Referenties

1. Sears, Zemansky. 2016. Universitaire natuurkunde met moderne natuurkunde. 14e. ED. Deel 1. 101-120.
2. Resnick, r. (1999). Fysiek. Vol. 1. 3 RA ED. in het Spaans. Continental Editorial Company s.NAAR. van C.V. 87-103.
3. Giancoli, D. 2006. Fysica: principes met toepassingen. 6e. ED. Prentice Hall. 72 - 96.
4. Hewitt, Paul. 2012. Conceptuele fysieke wetenschap. 5e. ED. Pearson.38-61.
5. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7e. ED. Cengage leren. 100 - 119.