Golfamplitude -kenmerken, formules en lichaamsbeweging

De Golfamplitude Het is de maximale verplaatsing die wordt ervaren door een punt in een golf ten opzichte van de evenwichtspositie. De golven manifesteren zich overal en vele manieren in de wereld om ons heen: in de oceaan, in het geluid en in het touw van een instrument dat het in het licht produceert, op het aardoppervlak en nog veel meer.

Een manier om golven te produceren en het gedrag ervan te bestuderen, is het observeren van de trillingen van een touw met een vaste einde. Door een verstoring aan het andere uiteinde te produceren, oscilleert elk deeltje van het touw en daarmee wordt de energie van de verstoring overgedragen in de vorm van een opeenvolging van pulsen overal.

Golven manifesteren zich in de natuur op veel manieren. Bron: Pixabay.

Naarmate de energie zich verspreidt, neemt het touw dat perfect elastisch moet zijn, de typische sinusvormige vorm aan met richels en valleien getoond in de figuur die hieronder in de volgende sectie verschijnt.

[TOC]

Kenmerken en betekenis van golfamplitude

De amplitude A is de afstand tussen de top en de referentieas of niveau 0. Indien voorkeur, tussen een vallei en de referentieas. Als de verstoring in het touw mild is, is de amplitude A klein. Als integendeel de verstoring intens is, zal de amplitude groter zijn.

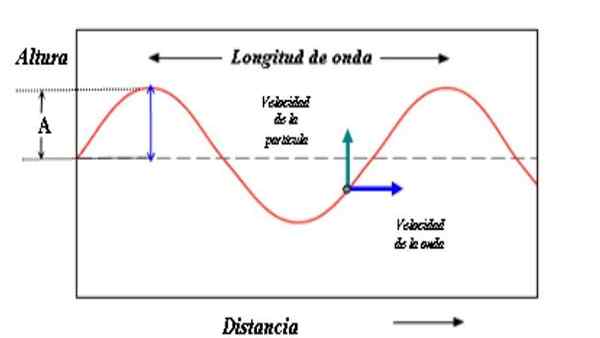Een model om de golf te beschrijven bestaat uit een sinusvormige curve. Golfamplitude is de afstand tussen een top of vallei en de referentieas. Bron: Paco [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/]]

De waarde van de amplitude is ook een maat voor de energie die de golf draagt. Het is intuïtief dat grote amplitude wordt geassocieerd met grotere energieën.

In feite is de energie evenredig met het kwadraat van de amplitude, die wiskundig tot uitdrukking komt:

Ik ∝a²

Kan u van dienst zijn: wederzijdse inductantie: formule/coëfficiënt, toepassingen, oefeningen

Waar ik de intensiteit van de golf is, op zijn beurt gerelateerd aan energie.

Het type golf geproduceerd in het voorbeeldtouw, behoort tot de categorie mechanische golven. Een belangrijk kenmerk is dat elk deeltje aan het touw altijd heel dicht bij de evenwichtspositie blijft.

De deeltjes bewegen niet of bewegen niet door het touw. Ze variëren op en neer. Dit wordt aangegeven in het topschema met de groene pijl, maar de golf samen met zijn energie, reist van links naar rechts (blauwe pijl).

Golven die zich in het water verspreiden, bieden het nodige bewijs om zich hiervan te overtuigen. Het observeren van de beweging van een vel dat in een vijver is gevallen, is te zien dat ze eenvoudig oscilleert bij de beweging van het water. Het gaat niet ver, althans duidelijk, dat er andere krachten zijn die andere bewegingen bieden.

Het golfmodel dat in de figuur wordt getoond, bestaat uit een repetitief patroon waarin de afstand tussen twee ribbels de golflengte λ. Als je wilt, scheidt de golflengte ook twee identieke punten van de golf, zelfs als ze niet op de top zijn.

De wiskundige beschrijving van een golf

Natuurlijk kan de golf worden beschreven door een wiskundige functie. Periodieke functies zoals sinus en cosinus zijn het ideaal voor de taak, of u de golf zowel in de ruimte als in de tijd wilt vertegenwoordigen.

Als we de verticale as in de figuur en de horizontale as noemen, noemen we het "t", dan wordt het gedrag van de golf in de loop van de tijd uitgedrukt door:

y = a cos (ωt + δ)

Voor deze ideale beweging oscilleert elk touwdeeltje met eenvoudige harmonische beweging, die afkomstig is van een kracht die recht evenredig is met de verplaatsing van het deeltje.

Kan u van dienst zijn: Dirac Jordan Atomic Model: kenmerken en postulaten

In de voorgestelde vergelijking zijn a, ω en δ parameters die de beweging beschrijven, zijnde naar de amplitude eerder gedefinieerd als de maximale verplaatsing die het deeltje heeft ervaren ten opzichte van de referentieas.

Het argument van de cosinus wordt genoemd Bewegingsfase En δ is de fase constant, Wat is de fase wanneer t = 0. Zowel de cosinusfunctie als de sinusfunctie zijn geschikt om een ​​golf te beschrijven, omdat ze alleen van elkaar verschillen π/2.

Het is meestal mogelijk om t = 0 te kiezen met Δ = 0 om de expressie te vereenvoudigen, verkrijgen:

y = a cos (ωt)

Wanneer de beweging herhaald is in zowel ruimte als tijd, is er een karakteristieke tijd die de Periode T, gedefinieerd als de tijd die het deeltje nodig heeft om een ​​volledige oscillatie uit te voeren.

Golfbeschrijving in tijd: karakteristieke parameters

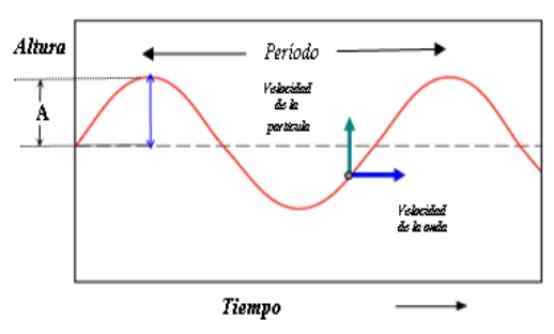Deze figuur toont de golfbeschrijving in de tijd. De afstand tussen ruggen (of valleien) komt nu overeen met de golfperiode. Bron: Paco [CC BY-SA 3.0 (http: // creativeCommons.Org/licenties/by-sa/3.0/]]

Nu herhalen zowel de borst als de cosinus zijn waarde wanneer de fase toeneemt in de waarde 2π, zodat:

ωt = 2π → ω = 2π /t

Ω wordt gebeld hoekfrequentie van beweging En het heeft dimensies van het omgekeerde tijd, zijnde eenheden in het internationale systeem radián / tweede of tweede^-1.

Eindelijk kun je de Bewegingsfrequentie F, als omgekeerde of wederzijdse van de periode. Vertegenwoordigt in het aantal ruggen per tijdseenheid, in welk geval:

F = 1/t

Ω = 2πf

Zowel F als Ω hebben dezelfde afmetingen en eenheden. Naast de tweede^-1, die Hertz of Hertzio wordt genoemd, het is gebruikelijk om over te horen Revoluties per seconde of revoluties per minuut.

Golfsnelheid v, die moet worden benadrukt dat het niet hetzelfde is als degene die de deeltjes ervaren, kan het gemakkelijk worden berekend als de golflengte λ en frequentie F bekend zijn:

Het kan je van dienst zijn: lichtgevende lichamen: kenmerken en hoe ze hun eigen licht genereren

V = λf

Als de oscillatie door de deeltjes van het eenvoudige harmonische type is, hangt de hoekfrequentie en de frequentie alleen af ​​van de aard van de oscillerende deeltjes en de kenmerken van het systeem. De amplitude van de golf heeft geen invloed op deze parameters.

Bij het spelen van een muzieknoot op een gitaar bijvoorbeeld, zal de noot altijd dezelfde toon hebben, hoewel het wordt aangeraakt met een grotere of mindere intensiteit, op deze manier zal een DO altijd klinken als een doen, hoewel het sterker of zachter wordt gehoord in een compositie, hetzij op een piano of op een gitaar.

In de natuur worden golven die in een materiële omgeving in alle richtingen worden getransporteerd verzwakt omdat de energie verdwijnt. Om deze reden neemt de amplitude af met het omgekeerde van de afstand R voor de bron, mogelijk zijn om dat te bevestigen:

A∝1/R

Oefening opgelost

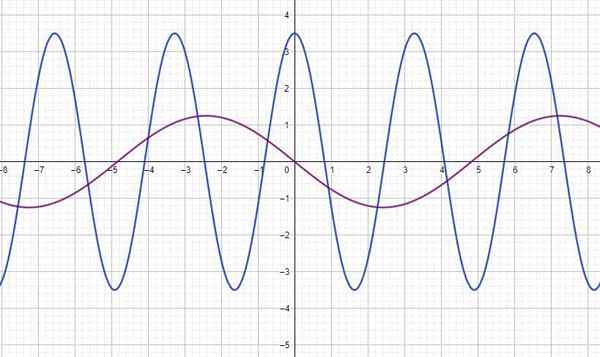
De figuur toont de functie y (t) voor twee golven, waar En is in meters en T in seconden. Voor elke zoek:

a) amplitude

b) periode

c) frequentie

d) De vergelijking van elke golf in termen van borsten of cosenos.

Antwoorden

a) Het wordt direct gemeten vanuit de grafiek, met behulp van het rooster: blauwe golf: a = 3.5m; Fuchsia Wave: A = 1.25 m

b) Het leest ook de grafiek, die de scheiding tussen twee pieken of valleien bepaalt, opeenvolgende: blauwe golf: t = 3.3 seconden; Fuchsia Wave T = 9.7 seconden

c) Het wordt berekend om te onthouden dat de frequentie de wederzijdse is van de periode: Blue Wave: F = 0.302 Hz; Fuchsia Wave: F = 0.103 Hz.

D) Blue Wave: Y (T) = 3.5 cos (ωt) = 3.5 cos (2πf.t) = 3.5 cos (1.9t) m; Fuchsia Wave: Y (T) = 1.25 Sin (0.65t) = 1.25 cos (0.65T+1.57)

Merk op dat de fuchsia -golf verouderd is π/2 ten opzichte van blauw, mogelijk om deze weer te geven met een sinusfunctie. Of verplaatst cosinus π/2.