Volume

We leggen uit wat het volume is, de formules, eenheden, hoe het te berekenen en verschillende voorbeelden te geven

Wat is het volume?

Hij volume van een lichaam is de numerieke waarde die de hoeveelheid ruimte meet die erdoor wordt ingenomen. De hoge, breedte en diepte bepalen het volume, hoe groter, hoe groter de bezette ruimte.

Het volume -concept is van groot belang, omdat de wereld drie -dimensionaal is en alle objecten breedte, hoogte en diepte hebben, daarom hebben ze volume. Mensen gebruiken het vaak, bijvoorbeeld door te schatten of het meubilair dat ze willen kopen, het in hun kamer past of dat ze een bepaalde kledingformaat betreden.

Op bepaalde gebieden van wetenschap en engineering, zoals bij het werken met vloeistoffen, of het nu vloeistoffen of gassen zijn, krijgt het bezette volume veel belang: bij het vullen van containers en pompvloeistoffen zoals water, of bij het ontwerpen van een schip voor een schip voor een schip. je zinkt niet. Dit alles maakt het essentieel om het voor veel processen te bepalen.

Er zijn formules om het volume van geometrische lichamen in reguliere vormen te berekenen, zoals prisma's, bollen, cilinders en kegels, bijvoorbeeld, afhankelijk van sommige van de afmetingen. En er zijn ook manieren om het volume van onregelmatige objecten te achterhalen, zoals iets later zal worden beschreven.

Volumeformules in geometrische figuren

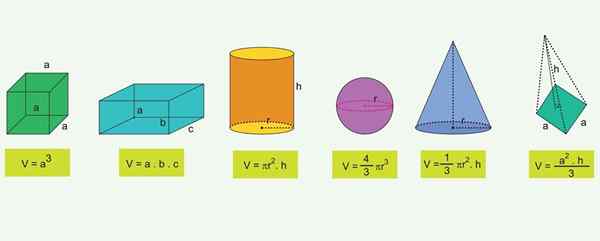Lijst van de meest voorkomende geometrische figuren en de formule van hun volumes

Voor de bekendste geometrische objecten zijn er formules die het volume kunnen berekenen:

• Kubus

V = ℓ³ 

Waarbij V het volume vertegenwoordigt en ℓ de rand (zijde) van de kubus is.

• Parallellepipedum

Een parallellepiped is een rechthoekige doos met breedte "A", lange ℓ en "H" hoogte. Het volume wordt gegeven door het product van zijn drie dimensies:

V = a ∙ ℓ ∙ ∙ H

• Gebied

Het volume van de bol hangt af van de straal R:

Kan u van dienst zijn: Nicolás Copernico

• Rechte cirkelvormige cilinder

Het volume van de rechte cirkelvormige cilinder is het product tussen het gebied van de basis en de hoogte "H". Omdat de basis een radioalbum "R" is, wiens gebied a = π · r is², Het volume blijft:

V = πr²∙ H

• Kutje

Het volume van de kegel is een derde van het product tussen het gebied van de cirkelvormige basis a en de hoogte h. Zoals a = πr², Dus:

• Piramide

Voor een piramide wiens basisgebied A is en een hoogte "H" heeft, wordt het volume gegeven door:

Als de piramide een vierkante basis heeft aan de zijkant "a", zoals in de figuur, is het basisgebied van de basis om² En het volume van de piramide is:

V = (1/3) ⋅A²⋅H

• Prisma

Het volume van het prisma is het product tussen het gebied van basis A en de hoogte "H":

V = a ∙ h

Volume -eenheden

In het internationale systeem van eenheden is de eenheid voor volume de kubieke meter of m³, Terwijl het in het Anglo -Saxon -systeem de kubieke voet of ft is³ (van Voeten, wat in het Engels "voet" betekent).

Er zijn veel andere eenheden, volgens de grootte van de bezette ruimte. Bijvoorbeeld km kubieke kilometer³ Voor grotere volumes of kubieke millimeter mm³ Voor kleine volumes. Er zijn ook lokale gebruikseenheden.

Het is ook noodzakelijk om de capaciteitseenheden te vermelden, nauw verwant aan die van volume, die bij voorkeur worden gebruikt voor vloeistoffen. De centrale capaciteitseenheid is de liter, afgekort L, die gelijkwaardig is aan een DM³ (Kubieke decimeter).

Andere eenheden die het vermelden waard zijn, zijn de gallon, de kubieke inch, de beker en de jicht, de laatste gebruikt om medicijnen te doseren.

Kan u van dienst zijn: vergelijkende methode

Hoe wordt volume gemeten?

Het volume van een lichaam, zoals elke andere maatregel, wordt uitgevoerd in vergelijking met een adequaat patroon, in dit geval een volume -eenheid.

De volume -eenheid wordt gedefinieerd als de kubus waarvan de rand 1 eenheid meet. Dit apparaat kan een meter, centimeter, voet, inch of een andere zijn. Vervolgens komt het volume van het object overeen met de hoeveelheid kubieke eenheden die door de figuur worden bezet en is het altijd een positief bedrag.

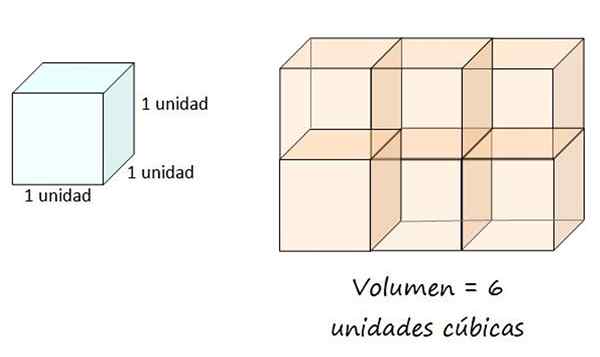Een kubieke eenheid wordt gedefinieerd als het volume van een emmer met rand gelijk aan 1, dus de doos aan de rechterkant heeft een volume van 6 kubieke eenheden. Bron: f. Zapata.

Volume van een geometrisch lichaam

Als het gaat om een ​​geometrisch lichaam zoals reeds vermeld, wordt het volume berekend door de juiste formule, met het meten van de dimensies aangegeven door de formule.

Als u bijvoorbeeld het volume van een bol wilt weten, is het noodzakelijk om zijn diameter te meten en daarmee is de straal bekend, dat is de helft. Als het een rechthoekige doos is, wordt de breedte, hoogte en diepte van hetzelfde gemeten.

Vervolgens worden de in de formule gevraagde waarden ingevoegd, zodat alle eenheden hetzelfde zijn, de vereiste bewerkingen worden uitgevoerd, er is het volume van het object.

Volume van een onregelmatig lichaam

Onregelmatige vaste stoffen hebben geen geometrische vorm, zoals een steen of een knipoog. Toch kunt u het volume vinden met behulp van een afgestudeerde container vol water, door middel van de vloeistofverplaatsingsmethode.

In de eerste plaats wordt het volume bezet door het water bepaald en wordt het onregelmatige object volledig ondergedompeld, waarbij het nieuwe volume wordt gemeten, dat groter is dan het origineel. Het volume van het onregelmatige object is het verschil tussen dit volume en dat van het water alleen.

Kan je dienen: Genie Wiley, het wilde meisje dat haar naam alleen herkende

Om deze methode te laten werken, mag het object niet worden gemaakt van elke stof die gemakkelijk in het water kan worden opgelost, moet het volledig ondergedompeld blijven en natuurlijk moet u een afgestudeerde container van de benodigde grootte hebben om het volledig te kunnen huisvesten.

Volume -voorbeelden

Het geschatte volume van sommige bekende objecten is:

• De aarde: 1.08321 × 10¹² km³
• Amazonas River: 225.000 m³/s (het volume per tijdeenheid wordt "flow" genoemd)
• Giza's geweldige piramide: 2.600.000 m³
• Een voetbal: 5600 cm³
• Een rugzak: 50 dm³

Volume en massa

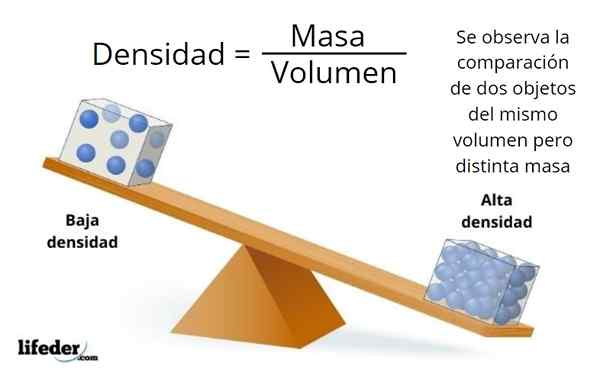
Het volume en de massa zijn geen synoniemen, de eerste is gekoppeld aan de afmetingen van het object en de tweede tot de hoeveelheid materie die het bevat.

Er kan veel materie zijn in een object van kleine dimensies, of heel weinig in een groot object, dat afhangt van de dichtheid van het materiaal, wat de verhouding is tussen de massa en het volume van een object:

Opgeloste oefeningen

Oefening 1

Bereken het volume van een rechthoekige doos waarvan de afmetingen 34 cm x 22 cm x 8 cm zijn.

• Oplossing

Het volume van een rechthoekige doos is gewoon het product van zijn drie dimensies:

V = 34 cm × 22 cm x 8 cm = 5984 cm³

Oefening 2

De basis van een vierhoekige piramide heeft een oppervlakte van 16 cm² En de hoogte is 6 cm. Bereken het volume van genoemde piramide.

• Oplossing

De hierboven gegeven formule voor het volume van een piramide wordt gebruikt, bekend het gebied van de basis:

En numerieke waarden worden vervangen:

V = (1/3) × 16 cm² × 6 cm = 32 cm³