Gemiddelde snelheidsformules, hoe het wordt berekend en opgelost oefening

De gemiddelde snelheid Voor een mobiel deeltje wordt het gedefinieerd als de reden tussen de variatie van de positie die ze ervaart en het tijdsinterval dat in de verandering wordt gebruikt. De eenvoudigste situatie is er een waarin het deeltje beweegt langs een rechte lijn vertegenwoordigd door de X -as.

Stel dat het mobiele object de X -posities inneemt₁ en x₂ In tijden T₁ en t₂ respectievelijk. De definitie van gemiddelde snelheid v_M Het wordt wiskundig als volgt weergegeven:

De eenheden van v_M In het internationale systeem zijn het meters/tweede (m/s). Andere gemeenschappelijke gebruikseenheden die verschijnen in mobiele teksten en apparaten zijn: km/u, cm/s, mijlen/u, voeten/s en meer, op voorwaarde dat ze de lengte/tijdvorm zijn.

De Griekse letter "Δ" leest "delta" en wordt gebruikt om het verschil tussen twee hoeveelheden samen te vatten.

[TOC]

Kenmerken van de gemiddelde snelheidsvector V_M

De gemiddelde snelheid is een belangrijk kenmerk van beweging. Bron: Pixabay

De gemiddelde snelheid is een vector, omdat deze gerelateerd is aan de verandering van positie, die op zijn beurt bekend staat als Vectorverplaatsing.

Deze kwaliteit wordt vetgedrukt weergegeven of door een pijl over de letter die de grootte aangeeft. In een dimensie is de enige mogelijke richting echter die van de X -as en kan daarom worden afgegeven met de vectornotatie.

Aangezien de vectoren grootte, richting en betekenis hebben, geeft een eerste blik op de vergelijking aan dat de gemiddelde snelheid dezelfde richting en zin zal hebben als de verplaatsing.

Stel je het deeltje voor van het voorbeeld dat langs een rechte lijn beweegt. Om uw beweging te beschrijven, is het noodzakelijk om een ​​referentiepunt aan te geven, dat de "oorsprong" zal zijn en wordt aangeduid als of.

Het deeltje kan weggaan of naderen of, naar links of naar rechts. U kunt ook veel of weinig tijd gebruiken om een ​​bepaalde positie te bereiken.

Het kan u van dienst zijn: hitte: formules en eenheden, kenmerken, hoe het wordt gemeten, voorbeelden

De genoemde magnitudes: positie, verplaatsing, interval van tijd en gemiddelde snelheid, beschrijven het gedrag van het deeltje tijdens het bewegen. Het gaat om de magnitudes Kinematisch.

Om de posities of locaties links van of het teken (-) te onderscheiden, wordt gebruikt en die aan de rechterkant van of het teken dragen (+).

De gemiddelde snelheid heeft een geometrische interpretatie die te zien is in de volgende figuur. Het is de helling van de lijn die door de P- en Q -punten gaat. Bij het snijden naar de positie versus positie. tijd op twee punten, het is een lijn drogen.

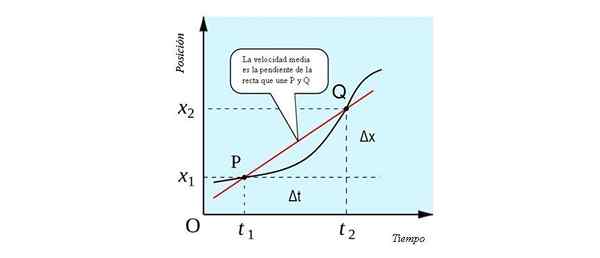Geometrische interpretatie van de gemiddelde snelheid, als een helling van de lijn die zich bij de P- en Q -punten verbindt. Bron: すじにく シチュー シチュー [CC0].

De tekenen van gemiddelde snelheid

Voor de volgende analyse moet er rekening mee worden gehouden T₂ > t₁. Dat wil zeggen, het volgende moment is altijd groter dan de stroom. Op deze manier T₂ - T₁ Het is altijd positief, wat meestal dagelijks zinvol is.

Dan wordt het teken van de gemiddelde snelheid bepaald door de X₂ - X₁. Merk op dat het belangrijk is.

Of "vooruit" of "terug", zoals de lezer liever.

Als de gemiddelde snelheid positief is, betekent dit dat gemiddeld de waarde van "X"Neemt toe in de loop van de tijd, hoewel dit niet betekent dat het op een bepaald moment in de beschouwde tijd zou kunnen zijn afgenomen - AT -.

Echter in globale termen, aan het einde van de tijd AT, Ze eindigde met een grotere positie dan degene die ze in het begin had. De details van de beweging worden in deze analyse genegeerd.

U kunt u van dienst zijn: de derde wet van Newton: aanvragen, experimenten en oefeningen

Wat als de gemiddelde snelheid negatief is? Welnu, het betekent dat het deeltje eindigt met een kleinere coördinaat dan die waarmee het begon. Groso -modus verplaatst achteruit. Laten we eens kijken naar enkele numerieke voorbeelden:

voorbeeld 1: Gezien de initiële en eindposities aangegeven, geeft u het teken van de gemiddelde snelheid aan. Waar ging het deeltje wereldwijd naartoe??

a) x₁ = 3 m; X₂ = 8 m

Antwoord: X₂- X₁  = 8 m - 3 m = 5 m. Positieve gemiddelde snelheid, het deeltje bewoog naar voren.

b) x₁ = 2 m; X₂ = -3 m

Antwoord: X₂ - X₁ = -3 m -2 m = -5 m. Gemiddelde negatieve snelheid, het deeltje bewoog achteruit.

 c) x₁  = - 5 m; X₂ = -12 m

Antwoord: X₂ - X₁   = -12 m -( -5 m) = -7 m. Gemiddelde negatieve snelheid, het deeltje bewoog achteruit.

d) x₁  = - 4 m; X₂ = 10 m

Antwoord: X₂ - X₁  = 10 m - (-4m) = 14 m. Positieve gemiddelde snelheid, het deeltje bewoog naar voren.

Kan de gemiddelde snelheid 0 zijn? Ja. Zolang het uitgangspunt en het aankomstpunt hetzelfde zijn. Betekent dit dat het deeltje noodzakelijkerwijs altijd in rust was?

Nee, het betekent alleen dat de reis retour was. Misschien reisde hij snel of misschien heel langzaam. Voor nu is het niet bekend.

De gemiddelde snelheid: een scalaire omvang

Dit leidt ons ertoe een nieuwe term te definiëren: de Gemiddelde snelheid. In de natuurkunde is het belangrijk om onderscheid te maken tussen de vectorgroottes en de magnitudes die dat niet zijn: de scalars.

Voor het deeltje dat de retour maakte, is de gemiddelde snelheid 0, maar het had erg snel kunnen zijn of misschien niet. Om het te weten, wordt de gemiddelde snelheid gedefinieerd als:

De eenheden van de gemiddelde snelheid zijn dezelfde als die van de gemiddelde snelheid. Het fundamentele verschil tussen beide magnitudes is dat de gemiddelde snelheid interessante informatie omvat over de richting en de richting van het deeltje.

Het kan u van dienst zijn: Fermionic Condensaat: eigenschappen, toepassingen en voorbeelden

Aan de andere kant biedt de gemiddelde snelheid alleen numerieke informatie. Met haar is het bekend hoe snel of langzaam het deeltje bewoog, maar niet als hij het voorwaarts of achteruit deed. Daarom is het een scalaire omvang. Hoe ze te onderscheiden om ze aan te duiden? Een manier is om vet te blijven voor vectoren, of een pijl op hen te plaatsen.

En het is belangrijk op te merken dat de gemiddelde snelheid niet gelijk hoeft te zijn aan de gemiddelde snelheid. Voor de retour is de gemiddelde snelheid nul, maar de gemiddelde snelheid doet het niet. Beide hebben dezelfde numerieke waarde wanneer ze altijd in dezelfde richting reizen.

Oefening opgelost

Je gaat rustig naar huis van school met 95 km/u per 130 km. Begin met regen en vermindert de snelheid tot 65 km/h. Hij komt eindelijk thuis na het rijden 3 uur en 20 minuten.

a) Hoe ver is uw schoolhuis?

b) Wat was de gemiddelde snelheid?

Antwoorden:

a) Sommige eerdere berekeningen zijn nodig:

De reis is verdeeld in twee delen, de totale afstand is:

D = D1+ D₂, Met d1 = 130 km

De totale tijd is 3 uur en 20 minuten = 3 + 1/3 uur = 10/3 uur = 3.33 uur (het is noodzakelijk om dezelfde eenheden voor tijd te plaatsen, in dit geval is het geschikt).

T2 = 3.33 - 1.37 uur = 1.96 uur

Berekening van D_2:

D₂ = 65 km/h x 1.96 h = 125. 4 km.

De school is d1+ d₂ = 255.4 km van het huis.

b) Nu kunt u de gemiddelde snelheid vinden:

Referenties

1. Giancoli, D. Natuurkunde. Principes met toepassingen. Zesde editie. Prentice Hall. 21-22.
2. Resnick, r. (1999). Fysiek. Deel 1. Derde editie in het Spaans. Mexico. Continental Editorial Company s.NAAR. van C.V. 20-21.
3. Serway, r., Jewett, J. (2008). Natuurkunde voor wetenschap en engineering. Deel 1. 7ma. Editie. Mexico. Cengage Learning Editors. 21-23.