Voortplantingssnelheid van een golf

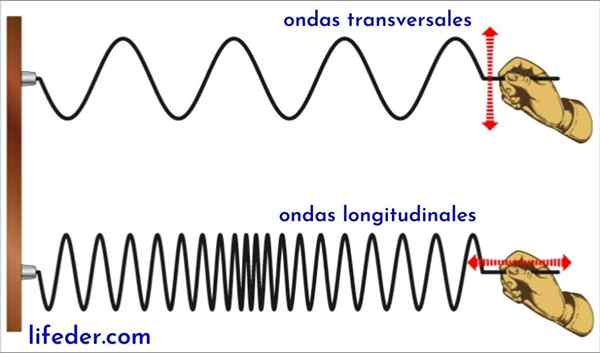
Voortplanting van een dwarse en longitudinale golf

Wat is de voortplantingssnelheid van een golf?

De Voortplantingssnelheid van een golf Het is de grootte die de snelheid meet waarmee de verstoring van de golf zich tijdens zijn verplaatsing verspreidt. De snelheid waarmee de golf zich verspreidt, hangt af van zowel het type golf als het medium waardoor het zich verspreidt.

Logisch gezien zal een golf die door de lucht beweegt die dit door de aarde of door de zee doet, niet met dezelfde snelheid bewegen. Evenzo gaat een seismische golf, geluid of licht niet op met dezelfde snelheid. Elektromagnetische golven verspreiden zich bijvoorbeeld met de snelheid van het licht; dat wil zeggen, op 300.000 km/s.

In het geval van geluid in de lucht is de voortplantingssnelheid 343 m/s. Over het algemeen hangt snelheid door een materiaal voor mechanische golven voornamelijk af van twee van de kenmerken van de omgeving: de dichtheid en de starheid ervan. In elk geval is de snelheid in het algemeen gerelateerd aan de waarde van de golflengte en de periode.

De relatie kan wiskundig worden uitgedrukt door het quotiënt: v = λ / t, waarbij v de snelheid van de golf is gemeten in meters per seconde, λ is de golflengte gemeten in meters en t is de periode gemeten in de tweede.

Hoe wordt de voortplantingssnelheid gemeten?

Over het algemeen wordt de snelheid van een golf bepaald door zijn golflengte en door zijn periode.

Aangezien de periode en de frequentie van een golf omgekeerd evenredig zijn, kan daarom ook worden bevestigd dat de snelheid afhankelijk is van de golffrequentie.

Kan u van dienst zijn: Dirac Jordan Atomic Model: kenmerken en postulaten

Deze relaties kunnen wiskundig worden uitgedrukt:

v = λ / t = λ ∙ f

In deze uitdrukking is f de frequentie van de golf gemeten in Hz.

Een dergelijke relatie is maar een andere manier om de relatie tussen snelheid, ruimte en tijd uit te drukken: V = S / T, waarbij S de ruimte voorstelt door een lichaam in beweging.

Daarom, om de snelheid te weten waarmee een golf zich verspreidt, is het noodzakelijk om zijn golflengte te kennen en, ofwel zijn periode of de frequentie. Uit het bovenstaande is het duidelijk dat snelheid niet afhangt van de energie van de golf of zijn amplitude.

Als het bijvoorbeeld gewenst is.

Factoren afhankelijk van de voortplantingssnelheid

Uiteindelijk zal de voortplantingssnelheid van een golf afhangen van zowel het type golf als de kenmerken van het medium waardoor het beweegt. Sommige specifieke gevallen worden hieronder blootgesteld.

Voortplantingssnelheid van kruisgolven op een touw

Een heel eenvoudig en zeer grafisch voorbeeld om te begrijpen wat de factoren zijn waarvan de snelheid van een golf van normaal afhangt, is die van de dwarse golven die langs een touw gaan.

De volgende uitdrukking maakt het mogelijk om de voortplantingssnelheid voor deze golven te bepalen:

v = √ (t / μ)

In deze uitdrukking is μ de lineaire dichtheid in kilogram per meter en T is de spanning van het touw.

Kan u van dienst zijn: subatomaire deeltjes

Gevoedingssnelheid

Geluid is een bepaald geval van mechanische golf; Daarom vereist het een middel om te bewegen, niet in staat om het in een vacuüm te doen.

De snelheid waarmee het geluid door een materiaalmedium reist, zal gebaseerd zijn op de kenmerken van het medium waardoor het wordt overgedragen: temperatuur, dichtheid, druk, vochtigheid, enz.

Het geluid beweegt sneller in vaste lichamen dan in vloeistoffen. Op dezelfde manier gaat het sneller naar vloeistoffen dan in gassen, zodat het sneller in water beweegt dan in de lucht

In het bijzonder is de snelheid van de voortplanting in de lucht 343 m/s wanneer deze zich bij een temperatuur van 20 ºC bevindt.

Voortplantingssnelheid van elektromagnetische golven

Elektromagnetische golven, die een soort transversale golven zijn, verspreiden zich door de ruimte. Daarom hebben ze geen middel nodig om te bewegen: ze kunnen door de leegte reizen.

Elektromagnetische golven gaan naar ongeveer 300.000 km/s (lichtsnelheid), hoewel ze, afhankelijk van hun snelheid, zijn gegroepeerd in frequentiebereiken die samenhangen met wat elektromagnetisch spectrum wordt genoemd.

Opgeloste oefeningen

Eerste oefening

Bereken de snelheid waarmee een dwarsgolf zich door een 6 m lang touw verspreidt, als de spanning van het touw 8 n is en de totale massa zijn 12 kg is.

Oplossing

Het eerste dat nodig is om te berekenen is de lineaire dichtheid van het touw:

 μ = 12/6 = 2 kg / m

Zodra dit is gedaan, is het al mogelijk om de voortplantingssnelheid te bepalen, waarvoor deze in de uitdrukking wordt vervangen:

Het kan u van dienst zijn: Live ladingen: concept, kenmerken, voorbeelden

v = √ (t / μ) = √ (8/2) = 2 m / s

Tweede oefening

Het is bekend dat de frequentie van de muzieknoot 440 Hz is. Bepaal wat zijn golflengte zowel in de lucht als in water is, wetende dat de voortplantingssnelheid in de lucht 340 m/s is, terwijl het in het water 1400 m/s bereikt.

Oplossing

Om de golflengte te berekenen die we wissen λ van de volgende uitdrukking:

V = λ ∙ f

Is verkregen: λ = v / f

Door de gegevens van de verklaring te vervangen, worden de volgende resultaten bereikt:

λ _lucht = 340 /440 = 0.773 m

λ _water = 1400/440 = 3,27 m